
Math Notebook
Key
Subtitle (#ff0000)
Formula(#f76b07)
Extra Info (#ffff00)
Sub-Subtitle (#28ff00)
example (#008000)
Title (#00e6ff)
Sub-Sub-Subtitle(#0014ff)
Read as… (#4B0082)
Super-Small title(#ff42f8)
Normal (#fffff)
Topics
Useful Tricks
Work out Percentage in your head (easy)
Multiply by 5, 25 and 125 easily
More
https://www.youtube.com/@tecmath
Quadratics
What are Quadratics
Quadratics are mathematical expressions or equations written in the form
ax² + bx + c = 0
note it must be x² not anything else

Solving Monics (a=1)
Monics are Quadratics where a = 1
ax² + bx + c = 0
e.g
x² + 10x + 16 = 0
Their are two steps to solve a quadratic equation:
Factorising
Using Zero Product property to Solve
……………………………………………………………………………………………………………..
1. Factorising
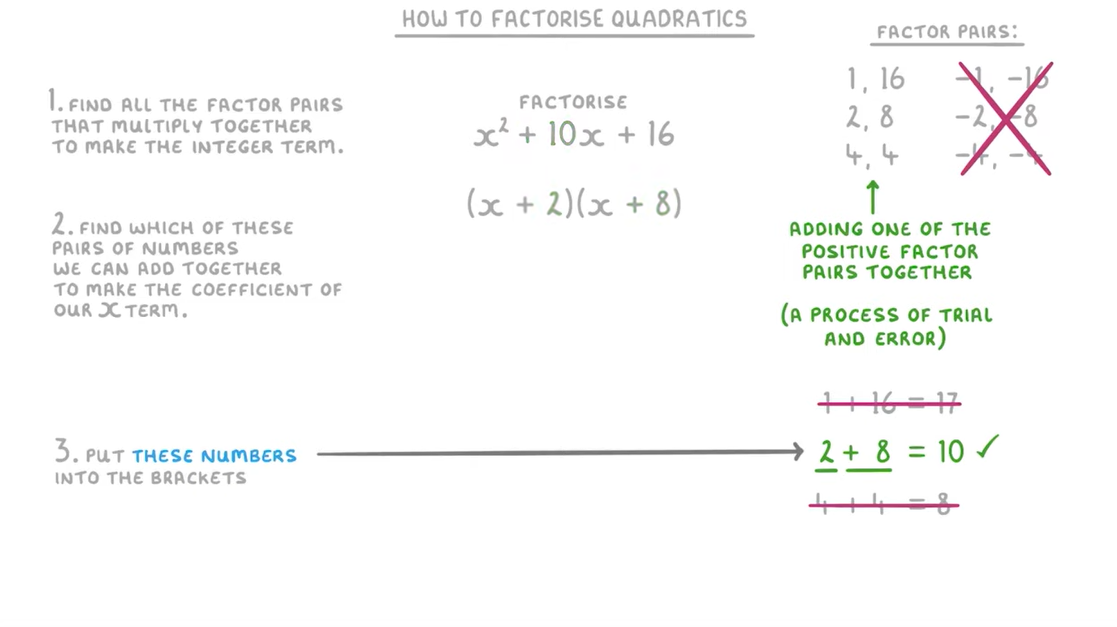
2. Solving Using Zero Product Property
Now that We have Factorised the equation from x² +10x + 16 = 0 to (x+2)(x+8) we can now solve it using the rule known as ZERO PRODUCT PROPERTY:
The Zero Product Property Rule
The Zero Product Property rule states that if ab = 0 either or both a=0 or b=0
this means that in factorised quadratics such as
(x+5)(x-4)=0
one of the brackets must be equal to 0
For this to happen x must be either -5 or 4 so our final answer is:
x = -5 or x = 4
but…
This only works if one of the sides is equal to 0 so before you factorise any equations make sure one of the sides is 0.
e.g:
x² + 8x = -24
would need to be converted to…
x² + 8x -24 = 0
This Means that x=-2 or x=-8
Solving Non-Monics (a≠1)

The Quadratic Formula
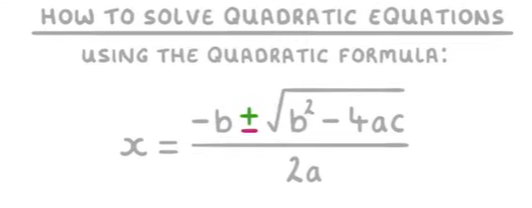
Perfect square expansion

D.O.T (Difference of Two Squares)
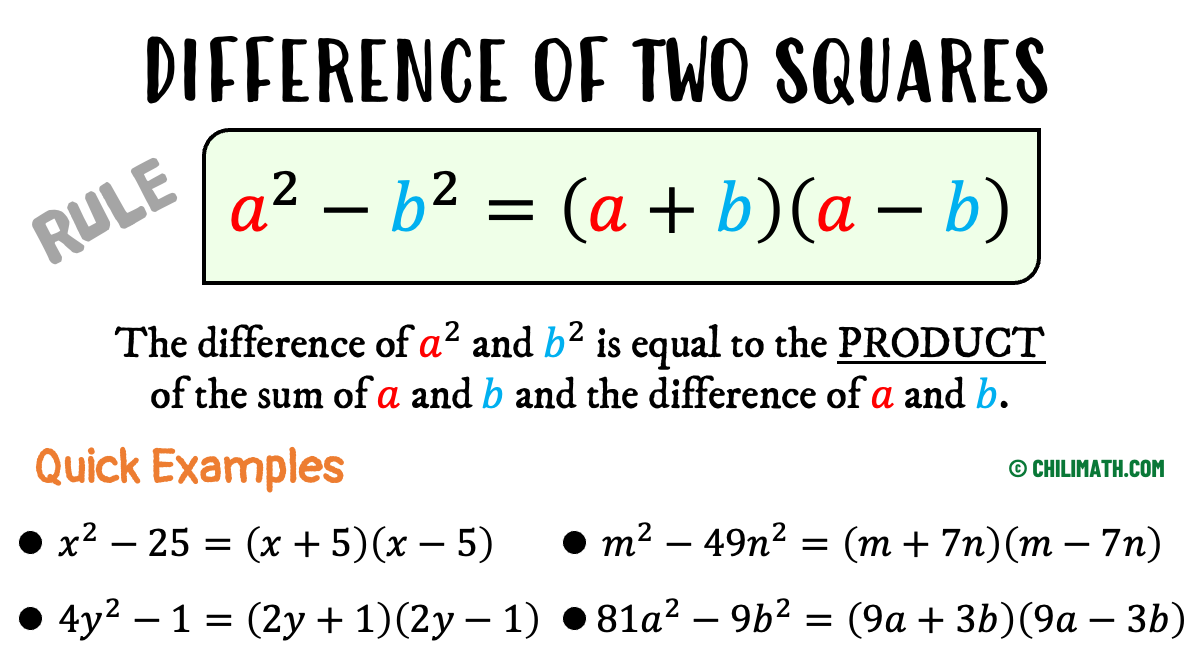
Quadratic graphs
Basics
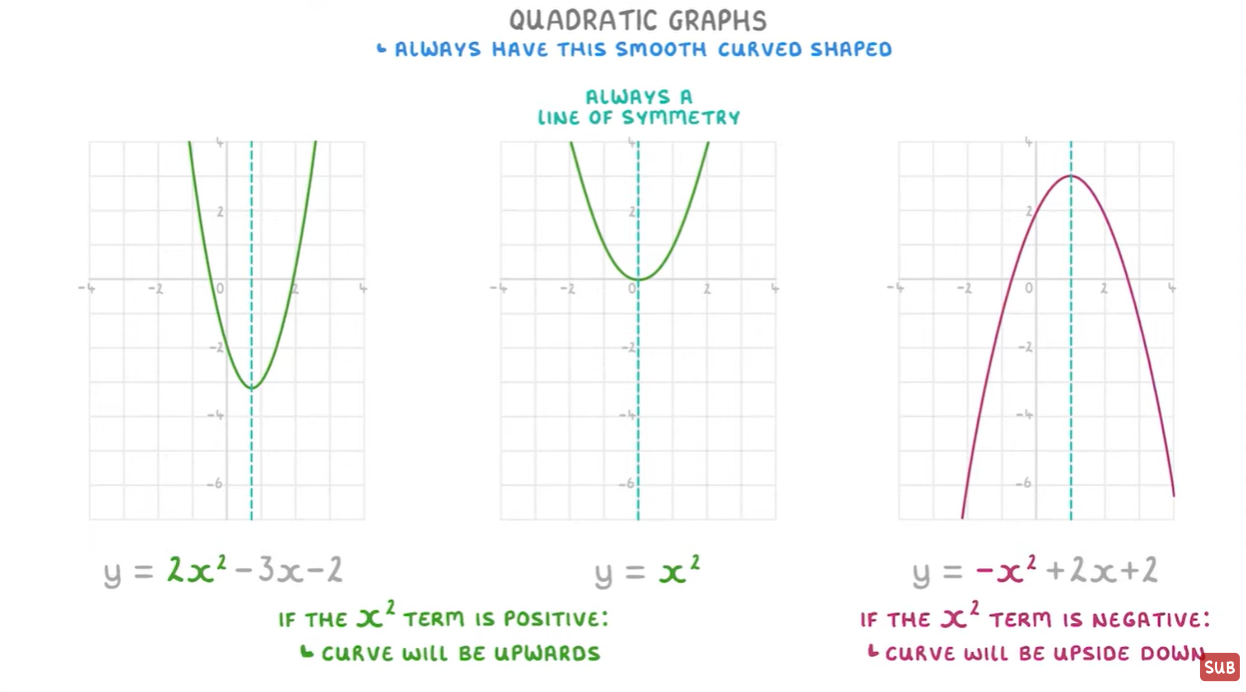
How The Equation Changes the Shape of The Graph
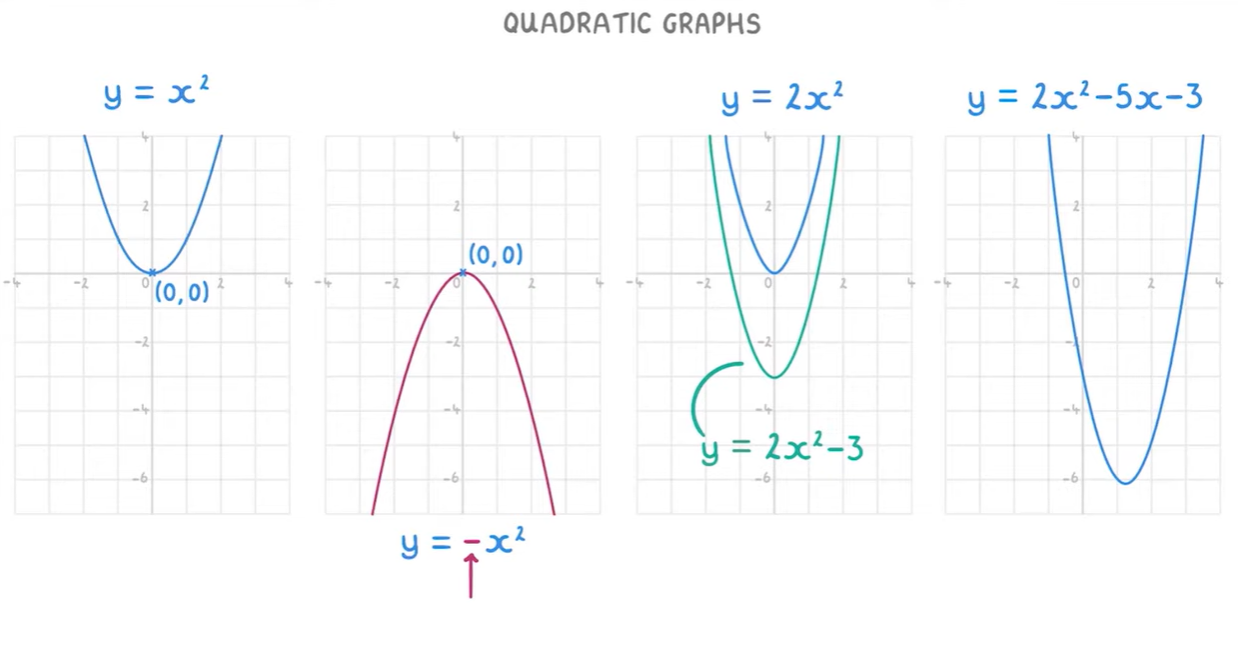
Plotting Quadratic Graphs
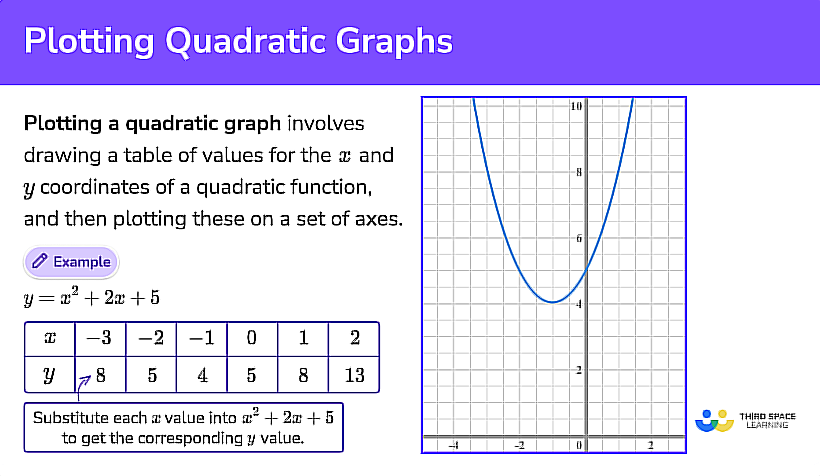
Parabola
Surds
What is a Surd
Surds are the irrational roots (√) of rational numbers

How to simplify Surds
How They Multiply and Divide:
To Know how to Simplify Surds you must first know how they Multiply and Divide:

Adding and Subtracting with Surds:

How to Simplify Surds:
now we Know how to multiply and divide them we can learn how to simplify them:

Example
√20 = √4×5 = √4×√5 = 2×√5 = 2√5
Summary:
The largest square Factor of 20 is 4 so factorise 20 into 4×5
Use the square root property √a × b = √a × √b
√4 = 2, leaving the final answer as 2√5.
How to Simplify Expressions Containing Surds

Rationalising the denominator

There are two different scenarios in which you can do this:
when the denominator contains just 1 surd

when the denominator contains more than just 1 surd
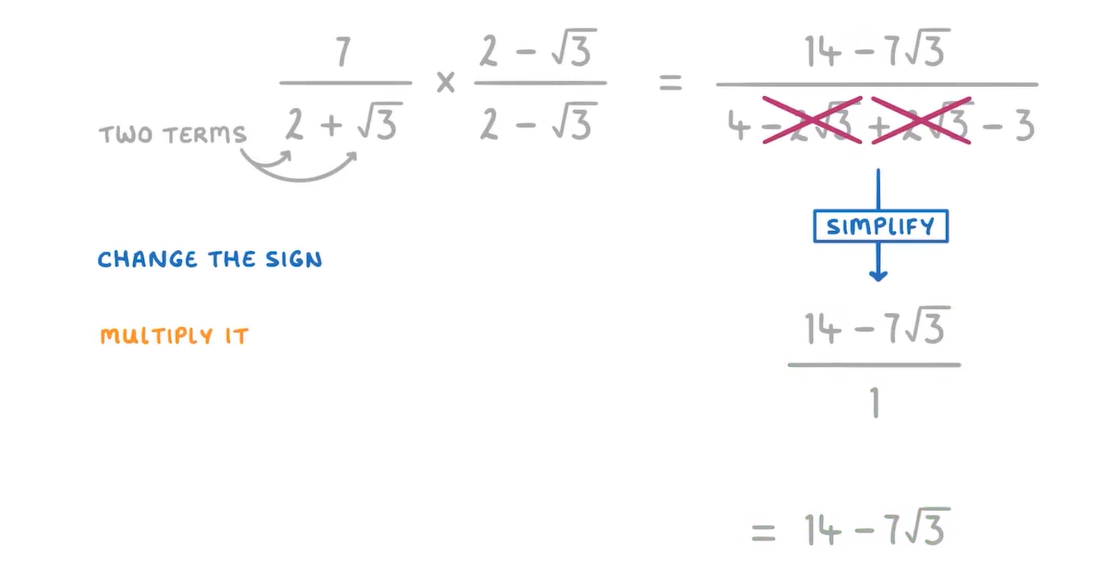
Bounds
Significant Figures

What are bounds

Error Intervals
An Error Interval is the range of values that a number could have taken before being rounded. This can be written as inequalities.
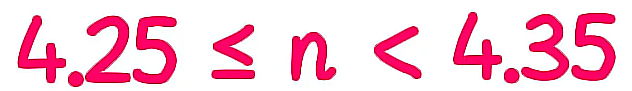
Calculations with bounds
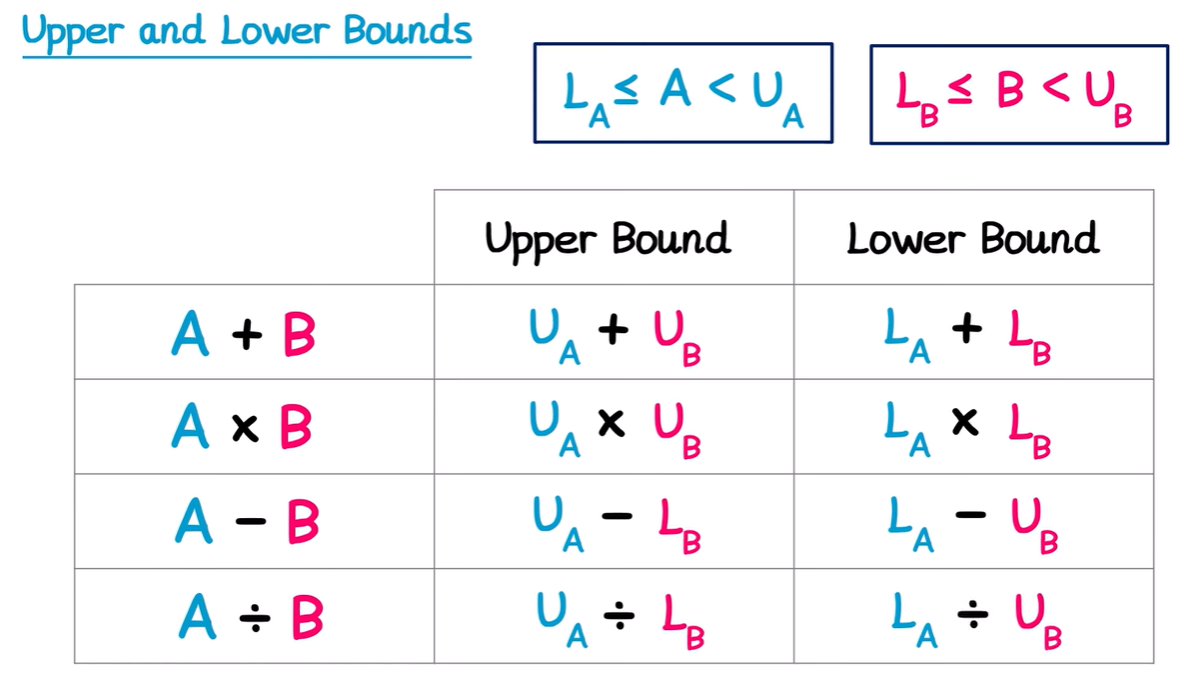
Bounds Formula
The Formula two work out bounds is:

……………………………………………………………………………………………………………………………….
Note: If the question asks to round to a certain decimal place (dp) or significant figures (sf), you use the place value:
For decimal places (dp): The place value is determined by the position of the last decimal place.
For example, rounding to 2 decimal places means the place value D is 0.01 because it's in the hundredths place
For significant figures (sf): The place value is determined by the position of the last significant figure.
For example, rounding to 3 significant figures means the place value D depends on the magnitude of the number, like D would be 1 for 3 significant figures in a number like 456, or 100 for 2 significant figures in a number like 9,326
Basic Example
Example:
A mass of 70 kg, rounded to the nearest 10 kg, has a lower bound of 65 kg, because 65 kg is the smallest mass that rounds to 70 kg. The upper bound is 75 kg * because 75 kg is the largest mass that would round down to 80kg.
I know 75kg rounds up not down but we still consider it the upper bound
How bounds add, multiply, subtract, divide
Complex Example 1 (Multiplication)

Final Answer:
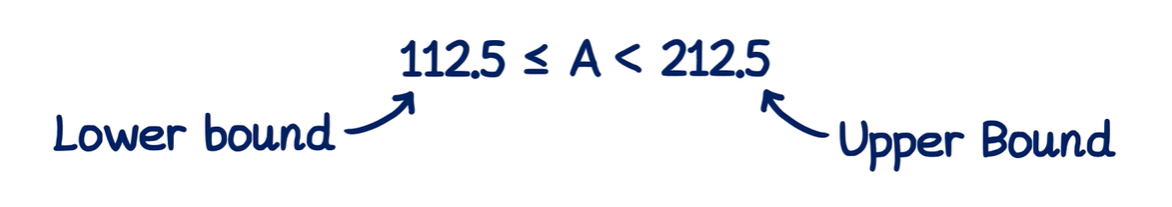
Complex Example 2 (Addition)

Complex Example 3 (Subtraction)

Complex Example 4 (Division)

Complex Example 5 (Algebra)

Standard Form
Intro To standard Form

How to express numbers in Standard Form

……………………………………………………………………………………………………………………………….
Examples


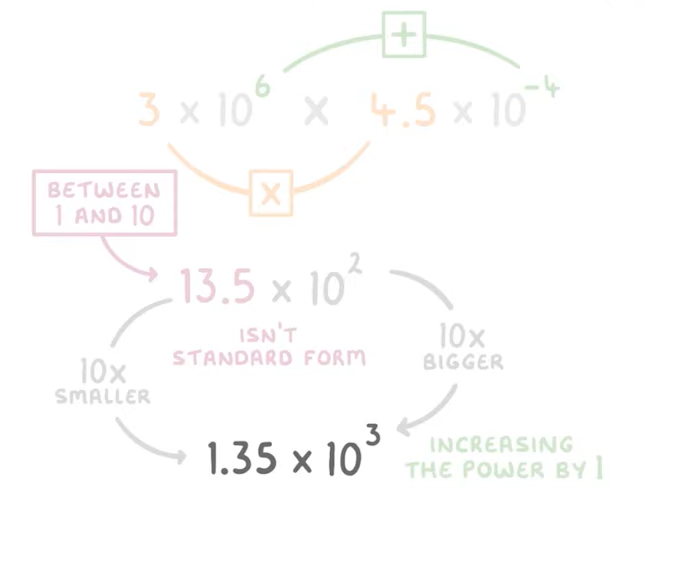
Multiplying And Dividing numbers in Standard Form

More Complex Examples

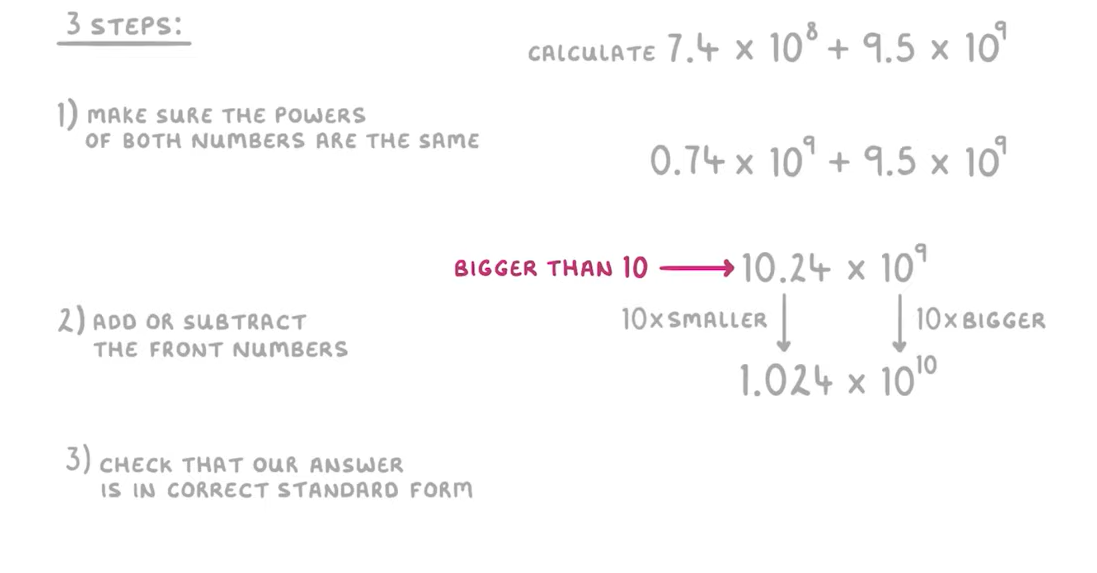
Adding and Subtracting in Standard Form
When Adding and Subtracting Standard Form there are 3 Rules:

Using these rules here are 2 examples
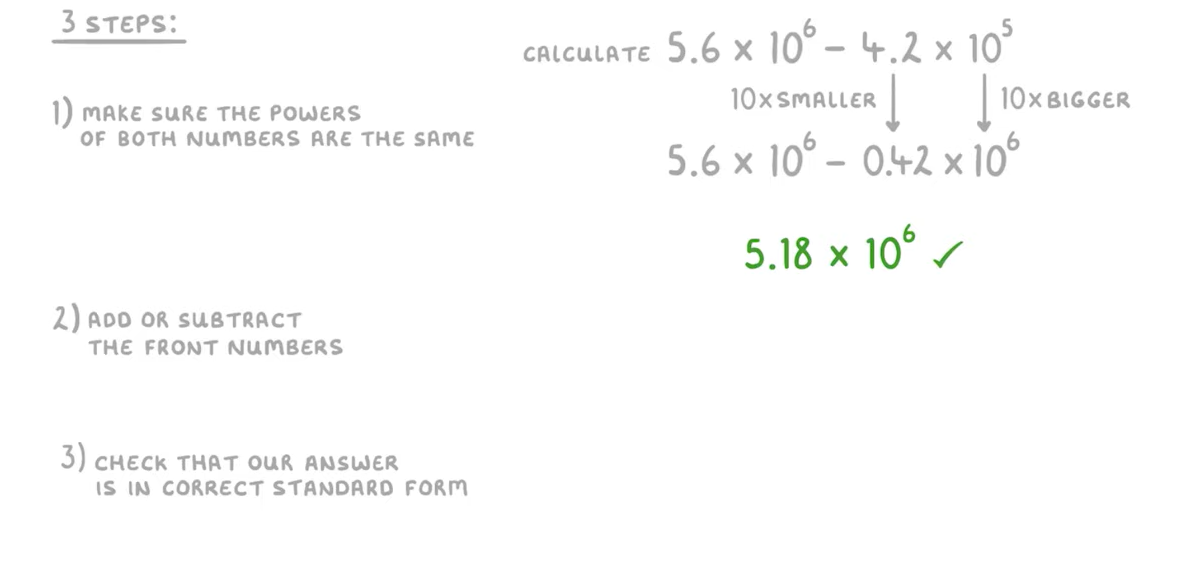
……………………………………………………………………………………………………………………………….
Indices
Using an index or power
An index, or a power, is the small floating number that goes next to a number or letter. The plural of index is indices.
Indices show how many times a number or letter has been multiplied by itself.
Here is a number written in index form:
2 is the base number and 4 is the index or power.
24 is a short way of writing 2×2×2×2.
a2 (read as 'a squared’) is a short way of writing a×a. a has been multiplied by itself.
a3 (read as ‘a cubed’) is a short way of writing a×a×a. a has been multiplied by itself three times.
a4 (read as ‘a to the power of 4') is a short way of writing a×a×a×a. a has been multiplied by itself four times, and so on.

Key fact
a1 (read as 'a to the power of 1') is written as simply a.
The 6 laws of indices
Law 1: multiplying indices
When the bases are the same
When multiplying indices, with the same base add the powers.
ab × ac = ab+c
1 Add the powers.
2 Multiply any coefficients.
………………………………………………………………………………………………………………………………
Example
Simplify 4a3 × 7a2
1. Add together the indices (3 and 2).
3+2=5
2. Multiply 4 and 7 together.
4×7=28
3. Now put that together
28a5
When the bases are different
When multiplying indices, with different bases there are two methods.
method 1-works for indices when the base and the powers are numbers:
2³ × 3² = 8 × 9 =72
convert the indices into regular numbers
multiply
method 2-works for indices when the base or/and the powers are different and letters:
You Can’t do It!
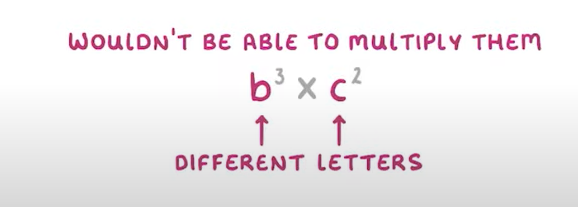
Law 2: dividing indices
when the bases are the same
When dividing indices, with the same base subtract the powers.
ab ÷ ac = ab-c
1 subtract the powers.
2 divide any coefficients.
………………………………………………………………………………………………………………………………
Example
Simplify 8a7 ÷ 8a4
1. subtract the indices (7 and 4).
7- 4=3
2. divide 8 and 8 .
8÷8=1
3. Now put that together
a3
when the bases are different
When dividing indices, with different bases there are two methods.
method 1-works for indices when the base and the powers are numbers:
2³ ÷ 3² = 8 ÷ 9 = 8/9
convert the powers to regular numbers
divide
method 2-works for indices when the base or/and the powers are different:
You Can’t do It!
law 3: raising powers

law 4: power of 0

law 5: negative indices

law 6: fractional indices

Probability
What is Probability

The Probability Scale

Probability Notation

All Possible Outcomes add up to 1

Example

How to Calculate Probability

Example

Relative Frequency
What is Relative Frequency

Are Relative Frequency and Probability the Same

Theoretical and Experimental Probability
Experimental Probability

Theoretical Probability

The More Trials The better


Listing Outcomes
Terms to Know

Sample space diagrams
I know the image says that sample space diagrams are tables but they can actually be a:
List
Table
any other organised diagram

The Product Rule

Venn diagrams
What are Venn diagrams
Universal Set (ξ)
The universal set is a rectangle outlining the space in which all values within the smaller sets are found. The universal set is denoted using the symbol ξ

Constructing Venn diagrams


Set Notation
Set notation is mathematical notation that is used in probability.
A set can be a list of items known as elements.
A subset would be a selection of these elements. The elements of a set could be a set of integers, shapes, people etc.
∈ means is an element of e.g 5∈A (Meaning 5 is an element of set A)
∉ means is not an element of e.g 5∉A (Meaning 5 is not an element of set A)
When we list elements within a set, we use these curly brackets { } and separate each element in the list with commas (,).
The universal set, ξ, is the list of every element that there is available to choose from.
(ξ is the Greek letter epsilon.)
For example,
Universal set, ξ, of integers from 1 to 12 is written as
ξ={1,2,3,4,5,6,7,8,9,10,11,12}.This set contains 12 elements.
If we wrote a subset of this set, for example A={prime numbers}, we would have the set A={2,3,5,7,11}. This set contains 5 elements. We use capital letters to define a subset.
The complement of a set is denoted to an apostrophe ‘. It would be the remaining elements in the universal set that are not part of that set.
The complement of A={prime number} from 1 to 12 would be the following set,
A′={1,4,6,8,9,10,12}. We can also say not set A.
We also have the empty set (or null set), ϕ, which contains no elements.
For example, from the universal set ξ={1,2,3,4,5,6,7,8,9,10,11,12}, the set
B={numbers greater than 12} = ϕ , because there are no numbers greater than 12 in the universal set.
There are other symbols that are used to describe set relationships.
The union, (∪), of the set of even numbers E={2,4,6,8,10,12}and multiples of 5,F={5,10} is the set E∪F={2,4,5,6,8,10,12}. Note that 10 appeared in both sets but we did not write it twice in the union. So the Union basically means ‘or’
The intersection, ∩, of the set of odd numbers O={1,3,5,7,9,11}and the set of prime numbers P={2,3,5,7,11} is the set O∩P={3,5,7,11}. To find the intersection of two or more sets, we find the elements that are contained within both/all of the sets only. So the Intersection basically means ‘and’
The cardinality of a set, n(A), is the number of elements in a set.
E.g If A={2,3,5,7,11}, n(A)=5.
Symbol | Description |
| Curly brackets - contain all items in a set |
| Comma - separates items in a set |
| Complement - the items not in a set |
| The Universal Set - contains all items in every set and subset required |
ϕ | The Empty Set - contains no items |
| Set A |
| Not Set A (the complement of Set A) |
| Set B |
| Not Set B (the complement of Set B) |
| A and B (A intersection B) |
| Not A and B (the complement of A intersection B) |
| A or B (A union B) |
| Not A or B (the complement of A union B) |
| The number of elements in A (The cardinality of A) |
| Element of - indicates an item is in a set |
| Not an element of - indicates an item is not in a set |
The ‘And’ + ‘Or’ Rules
Independent and Dependent events

The ‘And’ Rule

The ‘Or’ Rule

Frequency trees

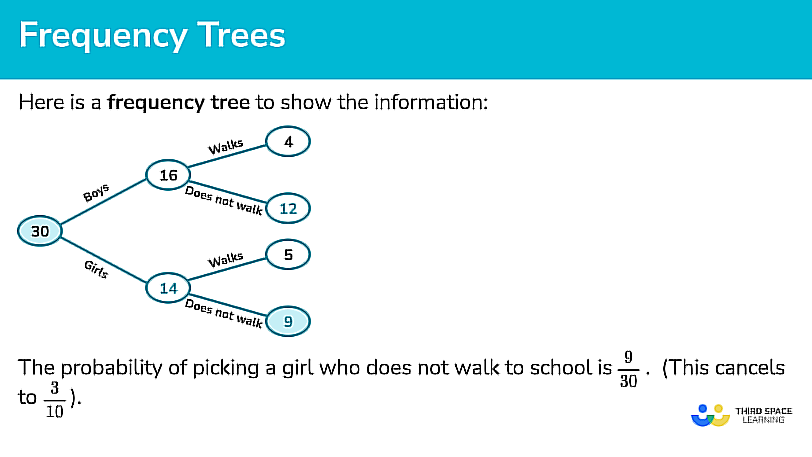
Tree Diagrams
Ratios + Proportion
Intro + how to simplify
Simplifying harder ratios
Converting ratios
to convert a ration to a fraction, decimal or percentage it must first be converted to a fraction and then into a decimal percentage so this video only covers how to convert a ratio into a fraction
Sharing in Ratio
Combining Ratios
Using Ratios
Problem Solving Using Ratios
More Problem Solving Using Ratios
Direct Proportion
Intro
Writing Equations With it
Inverse Proportion
Multiplicative Relationships
Compound Measures
Intro

Average Speed
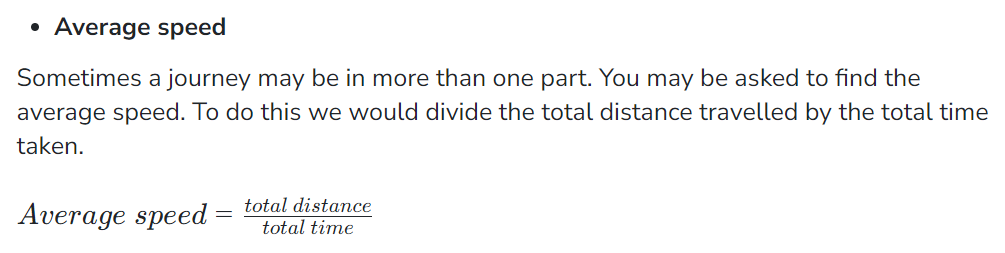

Converting Compound Units
Useful Links
Math Notebook
Key
Subtitle (#ff0000)
Formula(#f76b07)
Extra Info (#ffff00)
Sub-Subtitle (#28ff00)
example (#008000)
Title (#00e6ff)
Sub-Sub-Subtitle(#0014ff)
Read as… (#4B0082)
Super-Small title(#ff42f8)
Normal (#fffff)
Topics
Useful Tricks
Work out Percentage in your head (easy)
Multiply by 5, 25 and 125 easily
More
https://www.youtube.com/@tecmath
Quadratics
What are Quadratics
Quadratics are mathematical expressions or equations written in the form
ax² + bx + c = 0
note it must be x² not anything else

Solving Monics (a=1)
Monics are Quadratics where a = 1
ax² + bx + c = 0
e.g
x² + 10x + 16 = 0
Their are two steps to solve a quadratic equation:
Factorising
Using Zero Product property to Solve
……………………………………………………………………………………………………………..
1. Factorising

2. Solving Using Zero Product Property
Now that We have Factorised the equation from x² +10x + 16 = 0 to (x+2)(x+8) we can now solve it using the rule known as ZERO PRODUCT PROPERTY:
The Zero Product Property Rule
The Zero Product Property rule states that if ab = 0 either or both a=0 or b=0
this means that in factorised quadratics such as
(x+5)(x-4)=0
one of the brackets must be equal to 0
For this to happen x must be either -5 or 4 so our final answer is:
x = -5 or x = 4
but…
This only works if one of the sides is equal to 0 so before you factorise any equations make sure one of the sides is 0.
e.g:
x² + 8x = -24
would need to be converted to…
x² + 8x -24 = 0
This Means that x=-2 or x=-8
Solving Non-Monics (a≠1)

The Quadratic Formula
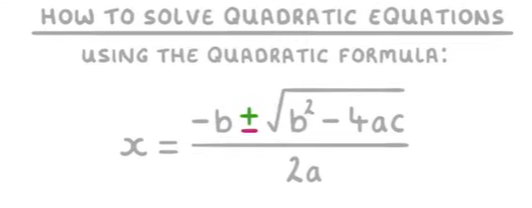
Perfect square expansion

D.O.T (Difference of Two Squares)
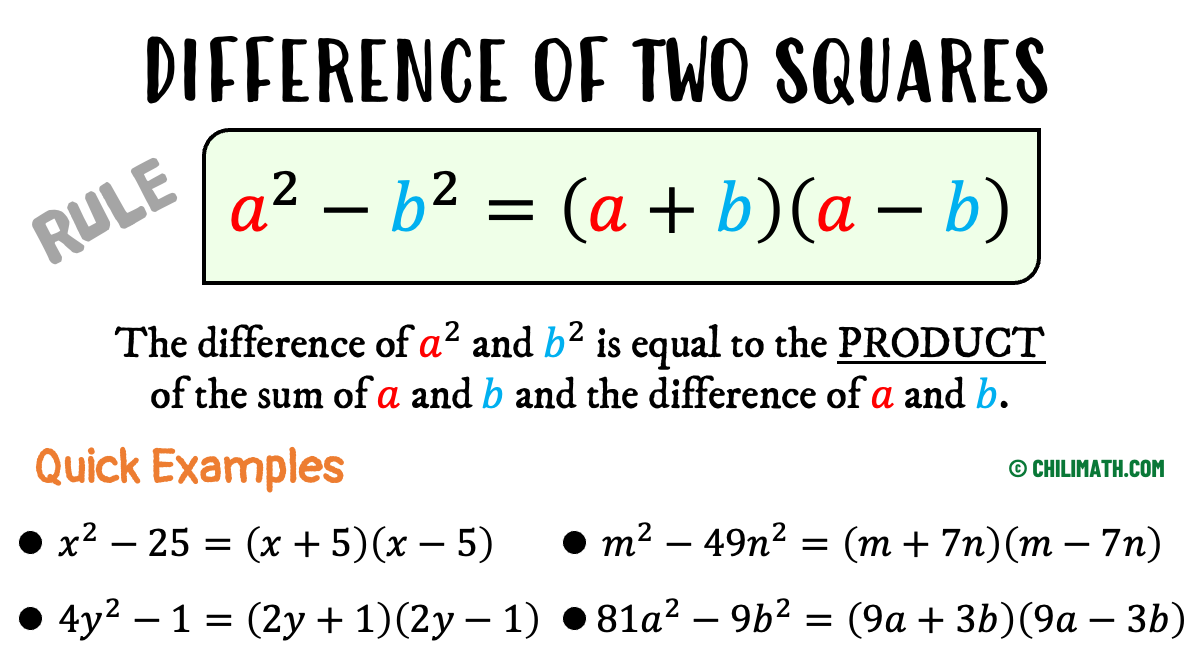
Quadratic graphs
Basics

How The Equation Changes the Shape of The Graph

Plotting Quadratic Graphs

Parabola

Surds
What is a Surd
Surds are the irrational roots (√) of rational numbers

How to simplify Surds
How They Multiply and Divide:
To Know how to Simplify Surds you must first know how they Multiply and Divide:

Adding and Subtracting with Surds:

How to Simplify Surds:
now we Know how to multiply and divide them we can learn how to simplify them:

Example
√20 = √4×5 = √4×√5 = 2×√5 = 2√5
Summary:
The largest square Factor of 20 is 4 so factorise 20 into 4×5
Use the square root property √a × b = √a × √b
√4 = 2, leaving the final answer as 2√5.
How to Simplify Expressions Containing Surds

Rationalising the denominator

There are two different scenarios in which you can do this:
when the denominator contains just 1 surd

when the denominator contains more than just 1 surd
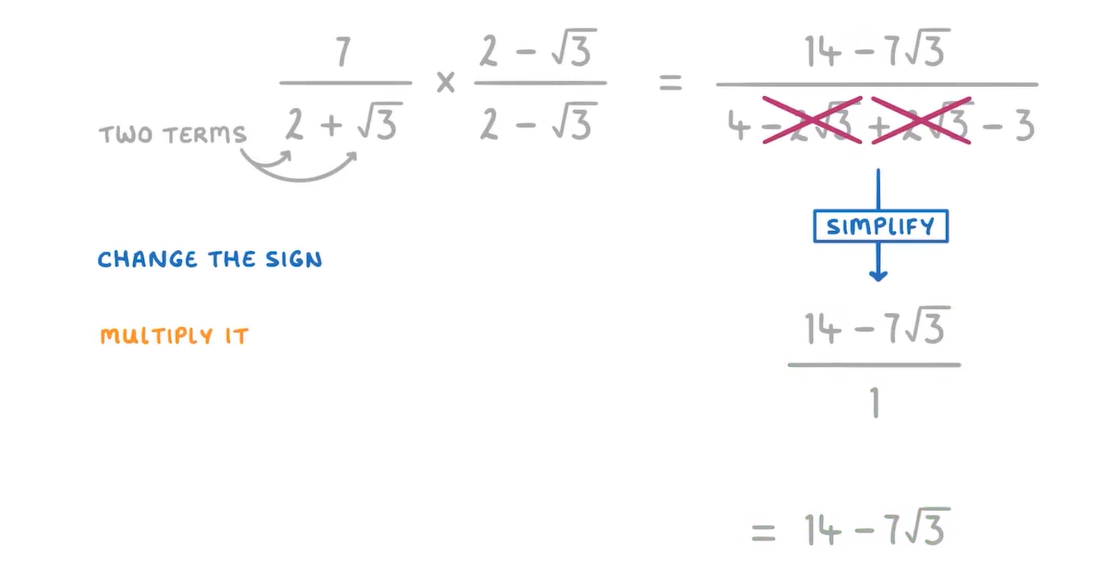
Bounds
Significant Figures

What are bounds

Error Intervals
An Error Interval is the range of values that a number could have taken before being rounded. This can be written as inequalities.
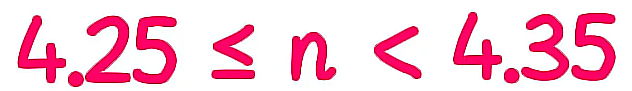
Calculations with bounds
Bounds Formula
The Formula two work out bounds is:

……………………………………………………………………………………………………………………………….
Note: If the question asks to round to a certain decimal place (dp) or significant figures (sf), you use the place value:
For decimal places (dp): The place value is determined by the position of the last decimal place.
For example, rounding to 2 decimal places means the place value D is 0.01 because it's in the hundredths place
For significant figures (sf): The place value is determined by the position of the last significant figure.
For example, rounding to 3 significant figures means the place value D depends on the magnitude of the number, like D would be 1 for 3 significant figures in a number like 456, or 100 for 2 significant figures in a number like 9,326
Basic Example
Example:
A mass of 70 kg, rounded to the nearest 10 kg, has a lower bound of 65 kg, because 65 kg is the smallest mass that rounds to 70 kg. The upper bound is 75 kg * because 75 kg is the largest mass that would round down to 80kg.
I know 75kg rounds up not down but we still consider it the upper bound
How bounds add, multiply, subtract, divide

Complex Example 1 (Multiplication)

Final Answer:
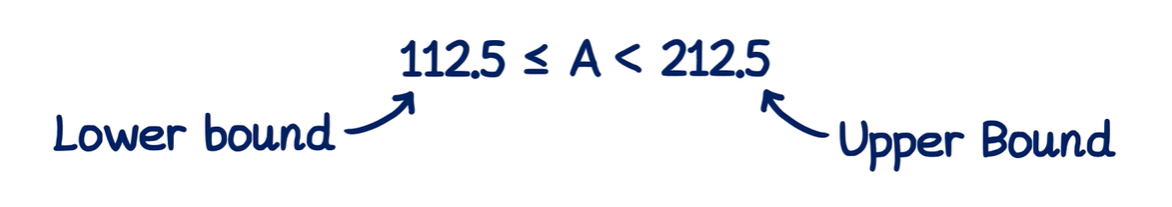
Complex Example 2 (Addition)

Complex Example 3 (Subtraction)

Complex Example 4 (Division)

Complex Example 5 (Algebra)

Standard Form
Intro To standard Form

How to express numbers in Standard Form

……………………………………………………………………………………………………………………………….
Examples


Multiplying And Dividing numbers in Standard Form

More Complex Examples


Adding and Subtracting in Standard Form
When Adding and Subtracting Standard Form there are 3 Rules:

Using these rules here are 2 examples
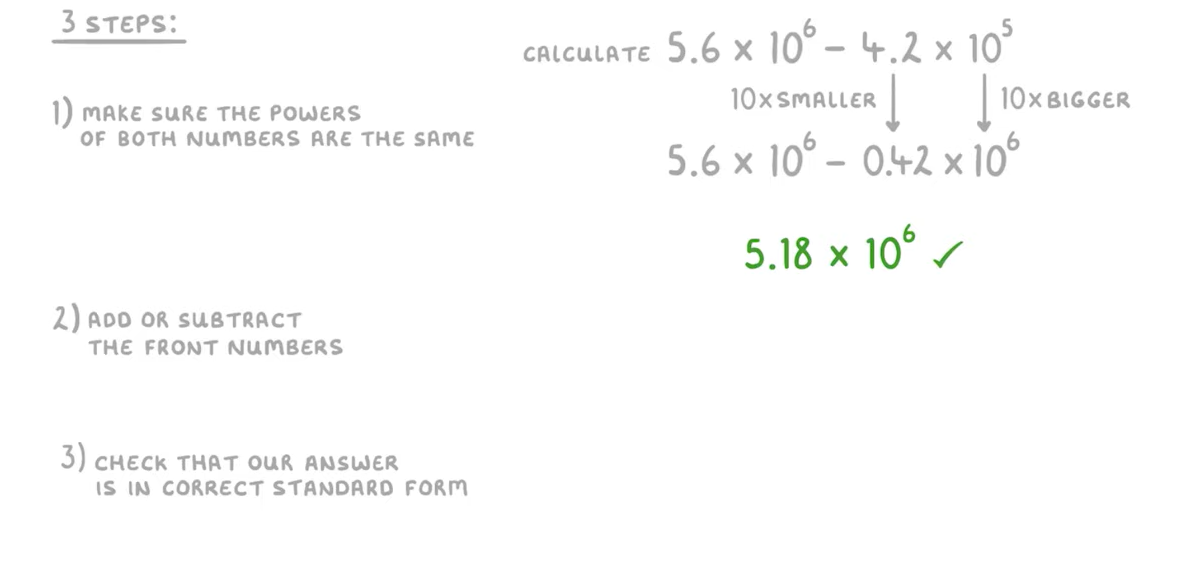
……………………………………………………………………………………………………………………………….

Indices
Using an index or power
An index, or a power, is the small floating number that goes next to a number or letter. The plural of index is indices.
Indices show how many times a number or letter has been multiplied by itself.
Here is a number written in index form:
2 is the base number and 4 is the index or power.
24 is a short way of writing 2×2×2×2.
a2 (read as 'a squared’) is a short way of writing a×a. a has been multiplied by itself.
a3 (read as ‘a cubed’) is a short way of writing a×a×a. a has been multiplied by itself three times.
a4 (read as ‘a to the power of 4') is a short way of writing a×a×a×a. a has been multiplied by itself four times, and so on.

Key fact
a1 (read as 'a to the power of 1') is written as simply a.
The 6 laws of indices
Law 1: multiplying indices
When the bases are the same
When multiplying indices, with the same base add the powers.
ab × ac = ab+c
1 Add the powers.
2 Multiply any coefficients.
………………………………………………………………………………………………………………………………
Example
Simplify 4a3 × 7a2
1. Add together the indices (3 and 2).
3+2=5
2. Multiply 4 and 7 together.
4×7=28
3. Now put that together
28a5
When the bases are different
When multiplying indices, with different bases there are two methods.
method 1-works for indices when the base and the powers are numbers:
2³ × 3² = 8 × 9 =72
convert the indices into regular numbers
multiply
method 2-works for indices when the base or/and the powers are different and letters:
You Can’t do It!
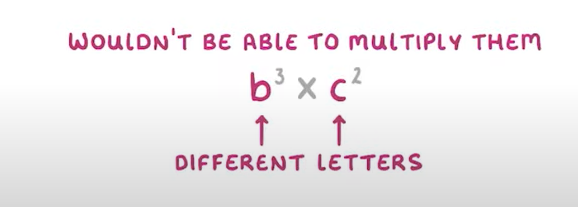
Law 2: dividing indices
when the bases are the same
When dividing indices, with the same base subtract the powers.
ab ÷ ac = ab-c
1 subtract the powers.
2 divide any coefficients.
………………………………………………………………………………………………………………………………
Example
Simplify 8a7 ÷ 8a4
1. subtract the indices (7 and 4).
7- 4=3
2. divide 8 and 8 .
8÷8=1
3. Now put that together
a3
when the bases are different
When dividing indices, with different bases there are two methods.
method 1-works for indices when the base and the powers are numbers:
2³ ÷ 3² = 8 ÷ 9 = 8/9
convert the powers to regular numbers
divide
method 2-works for indices when the base or/and the powers are different:
You Can’t do It!
law 3: raising powers

law 4: power of 0

law 5: negative indices

law 6: fractional indices

Probability
What is Probability

The Probability Scale

Probability Notation

All Possible Outcomes add up to 1

Example

How to Calculate Probability

Example

Relative Frequency
What is Relative Frequency

Are Relative Frequency and Probability the Same

Theoretical and Experimental Probability
Experimental Probability

Theoretical Probability

The More Trials The better


Listing Outcomes
Terms to Know

Sample space diagrams
I know the image says that sample space diagrams are tables but they can actually be a:
List
Table
any other organised diagram

The Product Rule

Venn diagrams
What are Venn diagrams

Universal Set (ξ)
The universal set is a rectangle outlining the space in which all values within the smaller sets are found. The universal set is denoted using the symbol ξ

Constructing Venn diagrams


Set Notation
Set notation is mathematical notation that is used in probability.
A set can be a list of items known as elements.
A subset would be a selection of these elements. The elements of a set could be a set of integers, shapes, people etc.
∈ means is an element of e.g 5∈A (Meaning 5 is an element of set A)
∉ means is not an element of e.g 5∉A (Meaning 5 is not an element of set A)
When we list elements within a set, we use these curly brackets { } and separate each element in the list with commas (,).
The universal set, ξ, is the list of every element that there is available to choose from.
(ξ is the Greek letter epsilon.)
For example,
Universal set, ξ, of integers from 1 to 12 is written as
ξ={1,2,3,4,5,6,7,8,9,10,11,12}.This set contains 12 elements.
If we wrote a subset of this set, for example A={prime numbers}, we would have the set A={2,3,5,7,11}. This set contains 5 elements. We use capital letters to define a subset.
The complement of a set is denoted to an apostrophe ‘. It would be the remaining elements in the universal set that are not part of that set.
The complement of A={prime number} from 1 to 12 would be the following set,
A′={1,4,6,8,9,10,12}. We can also say not set A.
We also have the empty set (or null set), ϕ, which contains no elements.
For example, from the universal set ξ={1,2,3,4,5,6,7,8,9,10,11,12}, the set
B={numbers greater than 12} = ϕ , because there are no numbers greater than 12 in the universal set.
There are other symbols that are used to describe set relationships.
The union, (∪), of the set of even numbers E={2,4,6,8,10,12}and multiples of 5,F={5,10} is the set E∪F={2,4,5,6,8,10,12}. Note that 10 appeared in both sets but we did not write it twice in the union. So the Union basically means ‘or’
The intersection, ∩, of the set of odd numbers O={1,3,5,7,9,11}and the set of prime numbers P={2,3,5,7,11} is the set O∩P={3,5,7,11}. To find the intersection of two or more sets, we find the elements that are contained within both/all of the sets only. So the Intersection basically means ‘and’
The cardinality of a set, n(A), is the number of elements in a set.
E.g If A={2,3,5,7,11}, n(A)=5.
Symbol | Description |
| Curly brackets - contain all items in a set |
| Comma - separates items in a set |
| Complement - the items not in a set |
| The Universal Set - contains all items in every set and subset required |
ϕ | The Empty Set - contains no items |
| Set A |
| Not Set A (the complement of Set A) |
| Set B |
| Not Set B (the complement of Set B) |
| A and B (A intersection B) |
| Not A and B (the complement of A intersection B) |
| A or B (A union B) |
| Not A or B (the complement of A union B) |
| The number of elements in A (The cardinality of A) |
| Element of - indicates an item is in a set |
| Not an element of - indicates an item is not in a set |
The ‘And’ + ‘Or’ Rules
Independent and Dependent events

The ‘And’ Rule

The ‘Or’ Rule

Frequency trees


Tree Diagrams
Ratios + Proportion
Intro + how to simplify
Simplifying harder ratios
Converting ratios
to convert a ration to a fraction, decimal or percentage it must first be converted to a fraction and then into a decimal percentage so this video only covers how to convert a ratio into a fraction
Sharing in Ratio
Combining Ratios
Using Ratios
Problem Solving Using Ratios
More Problem Solving Using Ratios
Direct Proportion
Intro
Writing Equations With it
Inverse Proportion
Multiplicative Relationships
Compound Measures
Intro

Average Speed


 Knowt
Knowt