Chapter 2- Motion Along a Straight Line
INTRODUCTION OF PHYSICS (2):
- One purpose of physics is to study the motion of objects which can be divided into two main categories: how fast an object moves, and how far an object travels in a given time.
- This principle is used in many ways, e.g. by geologists to measure movements of tectonic plates.
In the case where an object moves along a single axis, it is called one-dimensional motion.
MOTION
Everything in the world, even the things we feel are stationary, are in fact moving since the earth is moving with continuous rotation and revolution.
The different types of motions and their study is called kinematics which adequately arranges motions to avoid indiscipline.
There are three general properties of motion that are restricted in three ways:
- The motion is along a straight line only which may be vertical, horizontal or slanted but must be straight.
- Forces cause motion.
- The moving object is either a particle (such as an electron) or an object that moves like a particle (such that every portion moves in the same direction and at the same rate).
POSITION AND DISPLACEMENT
- To locate an object, we use its position relative to a particular reference point, usually the origin (zero point) of an axis, most commonly the x-axis.
- The positive direction of the axis is in the direction of increasing numbers (coordinates), and the opposite direction to the negative coordinates is the negative direction.
- A change from the position, e.g. from x1 to x2 is called the change in displacement.
- It is calculated by subtracting x2 (final velocity) from x1 (initial velocity), i.e. X2-X1.
- The displacement in a positive direction is always positive since x1 is smaller than x2, while displacement in the opposite direction is always negative since x2 is greater than x1.
- Displacement only involves initial and final positions, and not the distance involved. Therefore, it should not be confused with the number of meters.
- At the starting point, the displacement is zero, since the initial and final velocities are both the same.
- Displacement is a vector quantity. A vector quantity contains a both, magnitude and direction.
- The sign of the displacement shows its direction; the plus sign may not be written but the minus sign is always mentioned.
- If the signs are ignored, we are left with the magnitude of displacement.
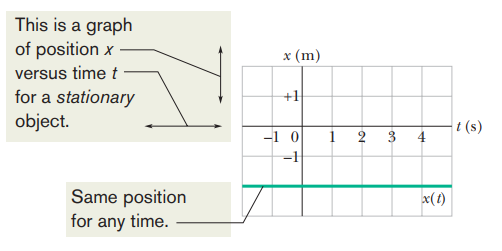
AVERAGE VELOCITY AND AVERAGE SPEED
Average velocity is the ratio of the change in displacement that occurs during a particular time interval, i.e, final - initial velocity/ time taken.
The unit for average velocity is the same as speed, m/s.
Average speed is another way to describe ‘how fast’ an object is moving.
Instead of displacement, speed deals with distance. It is the rate of change of distance over a particular time, i.e. total distance covered/ total time taken.

GRAPHS FOR AVG VELOCITY
- Average velocity is another vector quantity with both, a magnitude and direction.
- If displacement (x m/s)is plotted against time (t s), a line with a slope/gradient will be obtained which tells the magnitude of the average velocity.
- This slope connects two points on the graph: one that corresponds to x1 and t1, and another that corresponds x2 and t2.
- If the slope is positive (the line is going upwards), the displacement and average velocity is positive.
- If the slope is negative (the line is going downwards), the displacement and average velocity is negative.
- Average velocity has the same sign as displacement since time is always positive.
INSTANTANEOUS VELOCITY AND SPEED
To describe ‘how fast’ an object moves, we use average speed and velocity. Most of the times however, we need a particular value of velocity at an exact given time, i.e. an instant.
How fast a particle is moving at a given instant is called instantaneous velocity.
The velocity at any instant is obtained from the average velocity by shrinking the time interval delta t closer and closer to 0. As t decreases, the average velocity approaches a limiting value, which is the velocity at that instant.

Note that v is the rate at which position x is changing with time at a given instant, i.e. v is the derivative of x with respect to t.
Also, v at any instant is the slope of the position–time curve at the point representing that instant. Velocity is another vector quantity.
Speed is the magnitude of velocity, i.e. speed is velocity without any direction. For instance, a velocity of 3 m/s and one of -3 m/s both have an associated speed of 3 m/s.
ACCELERATION
A particle is said to undergo acceleration when its velocity changes.
Acceleration of a particle at any instant is the rate at which its velocity is changing at that instant.
Graphically, the acceleration at any point is the slope of the curve of v(t) at that point.
The formula of acceleration is the change in velocity upon the change in time, i.e. the derivative of velocity with respect to time or the second derivative of its displacement x(t) with respect to time.
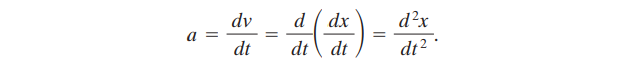
Unit of acceleration is m/s^2 .
Acceleration is also a vector quantity.
Its algebraic sign represents its direction on an axis (just as in velocity), and the gradient of its curve on the graph represents its magnitude.
Our bodies react to change in acceleration but not to change in velocity, for e.g. When you are in a car traveling at 90 km/h or an airplane traveling at 900 km/h, you have no bodily awareness of the motion. However, if the car or plane quickly changes velocity, you may become keenly aware of the change.
Large accelerations are sometimes expressed in terms of g units, with 1g = 9.8 m/s^2.
If the signs of the velocity and acceleration of a particle are the same, the speed of the particle increases. If the signs are opposite, the speed decreases but the object may or may not be moving in the opposite direction.
THE UNIQUE CASE OF CONSTANT ACCELERATION
In most cases, acceleration is either constant or approximately so.
This is so common that a special set of equations have been derived for it. It is to be remembered that these equations are valid only for constant acceleration or approximately so.
When the acceleration is constant, the average acceleration and instantaneous acceleration are equal and we can write it as:

The average velocity over any time interval is the average of the velocity at the beginning of the interval and the velocity at the end of the interval. The average velocity can then be calculated as:
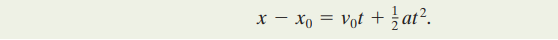
Another equation that can be used is:


FREE FALL ACCELERATION
Free-fall acceleration is the rate at which an object would fall if all the effects of air on it could be ignored, i.e. in a vacuum.
Its magnitude is represented by g.
The acceleration of free fall is the same for all objects, regardless of its mass, density, or shape.
For free fall:
(1) The directions of motion are now along a vertical y-axis instead of the x-axis, with the positive direction of y upward.
(2) The free-fall acceleration is negative—that is, downward on the y axis, toward Earth’s center—and so it has the value -g in the equations.
For graphical integration,
