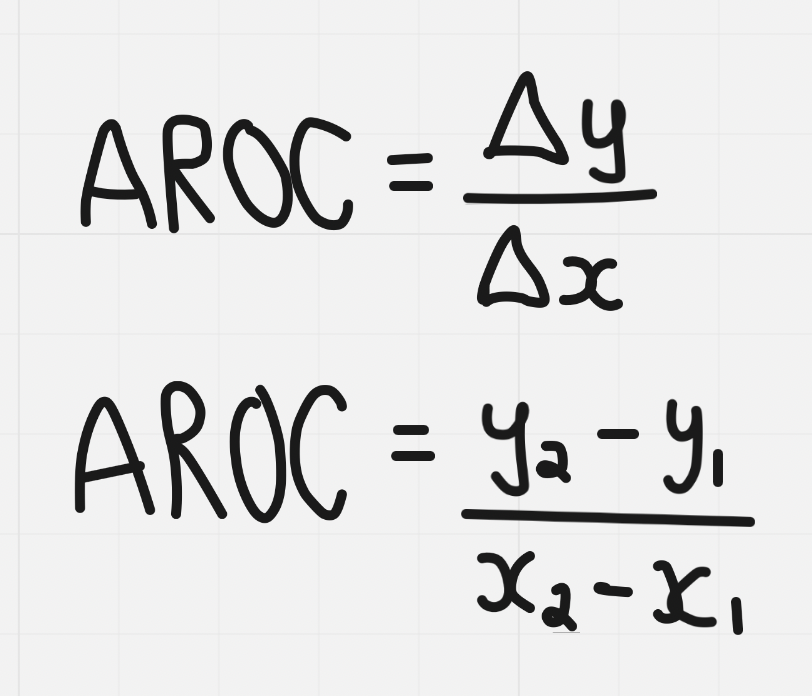12-01: Polynomial Functions
A polynomial expression has the general form:
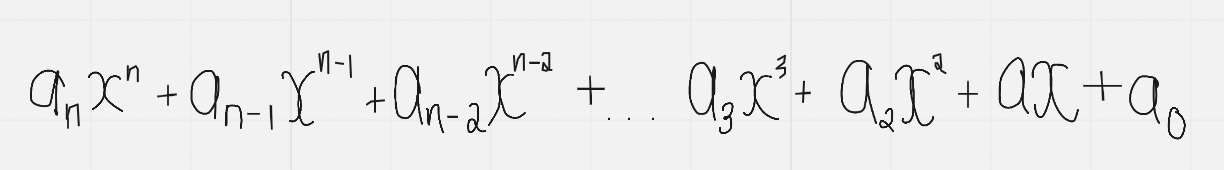
Where….
n: exponent (degree: the largest exponent)
x: variables
a₁ , a₂ : coefficient, a value multiplied by a variable
aₒ : constant, have no variable
aₙ : leading coefficient (LC), in front of the largest degree term
Criteria for Polynomial Expressions
- Has only positive whole number exponents
- Has no special features (e.g. sin, |x|, etc)
- Has no x in the denominator (i.e. no 1/x) or as an exponent (i.e. no 5ˣ)
Power Functions
- Power functions: Polynomial functions with just one term, the simplest single term polynomials
y = axⁿ a ≠ 0
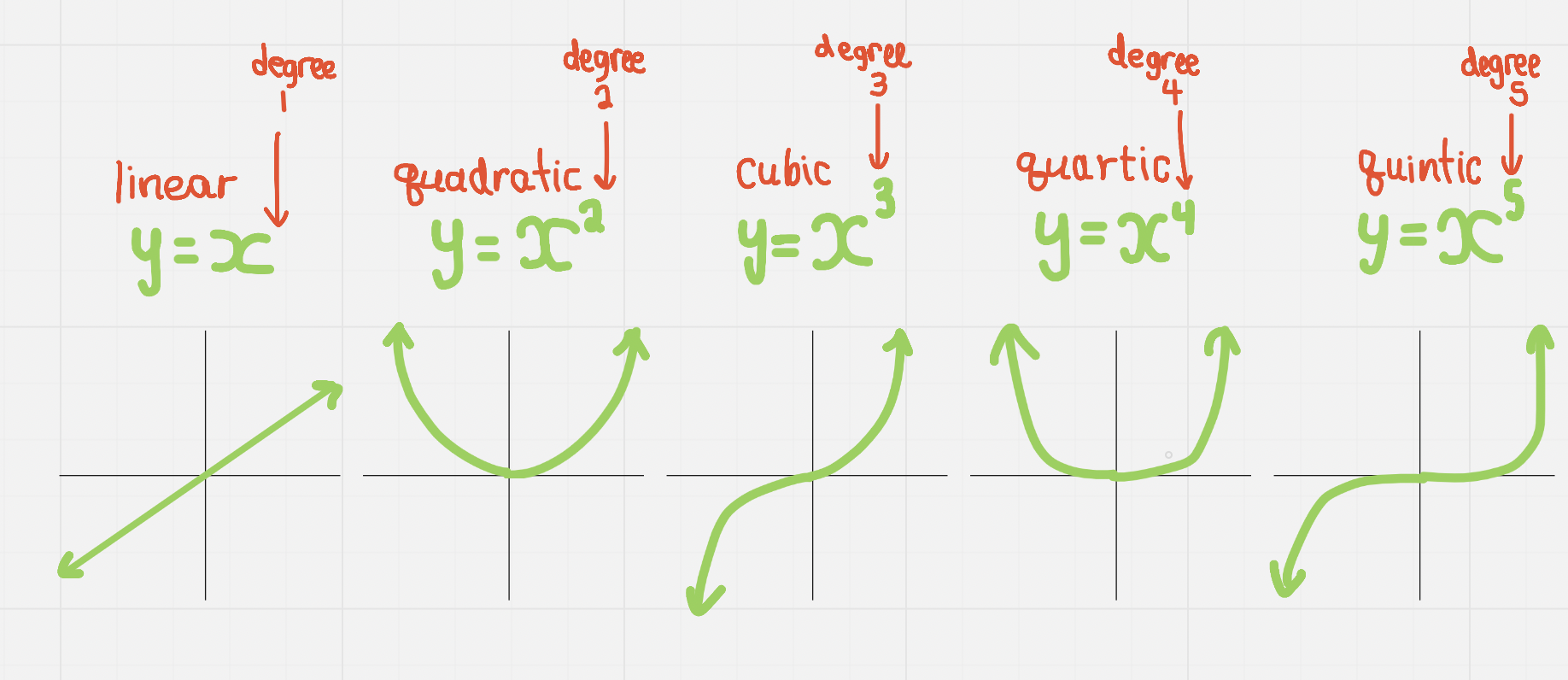
As we can see, there is a pattern depending on whether something has an even or odd degree
Power Function Features
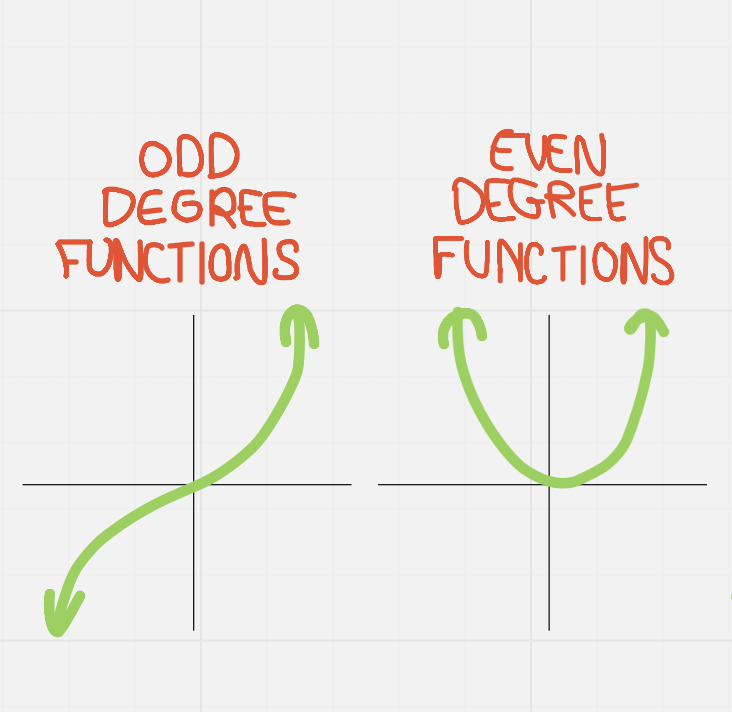
Power functions have similar characteristics depending on whether their degree is odd or even (referred to as an ==“odd degree function”== or as an ^^“even degree function”^^ → this also may influence other characteristics
They roughly look like:
Domain (in interval notation)
Regardless of whether a function is an ==odd== or ^^even^^ degree function, its domain will always be the same
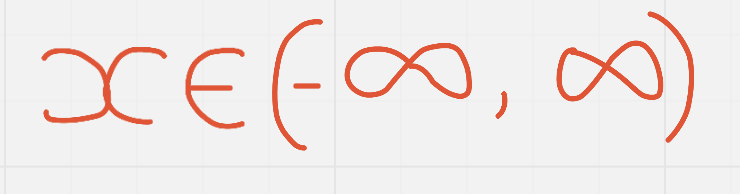
Range (in interval notation)
When you have an ==odd== degree function:
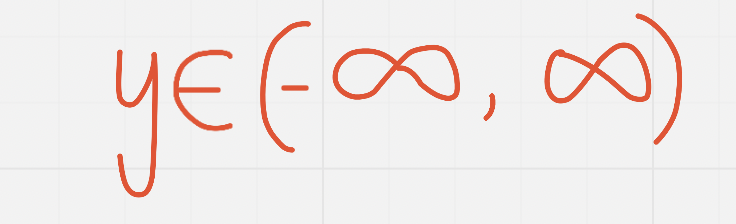
When you have an ^^even^^ degree function

Symmetry
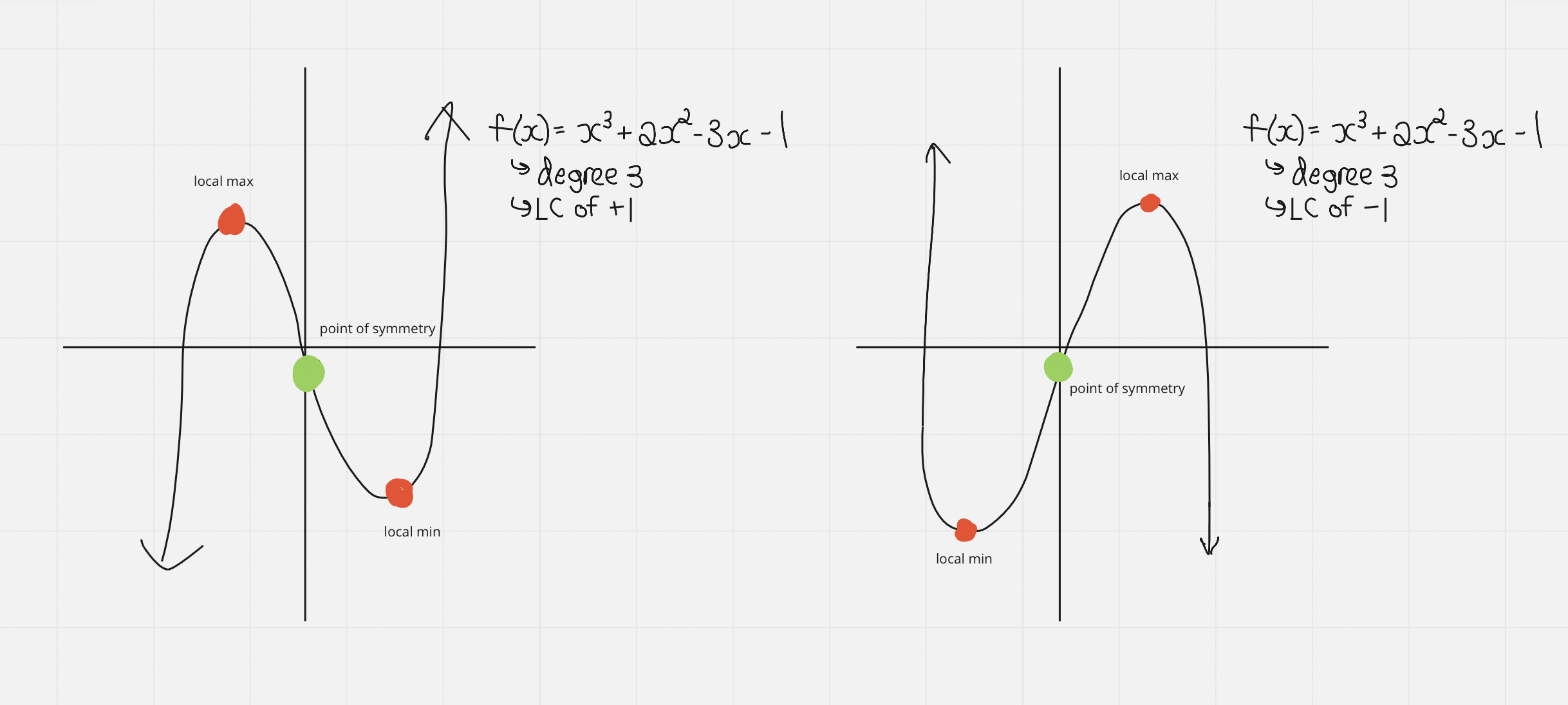
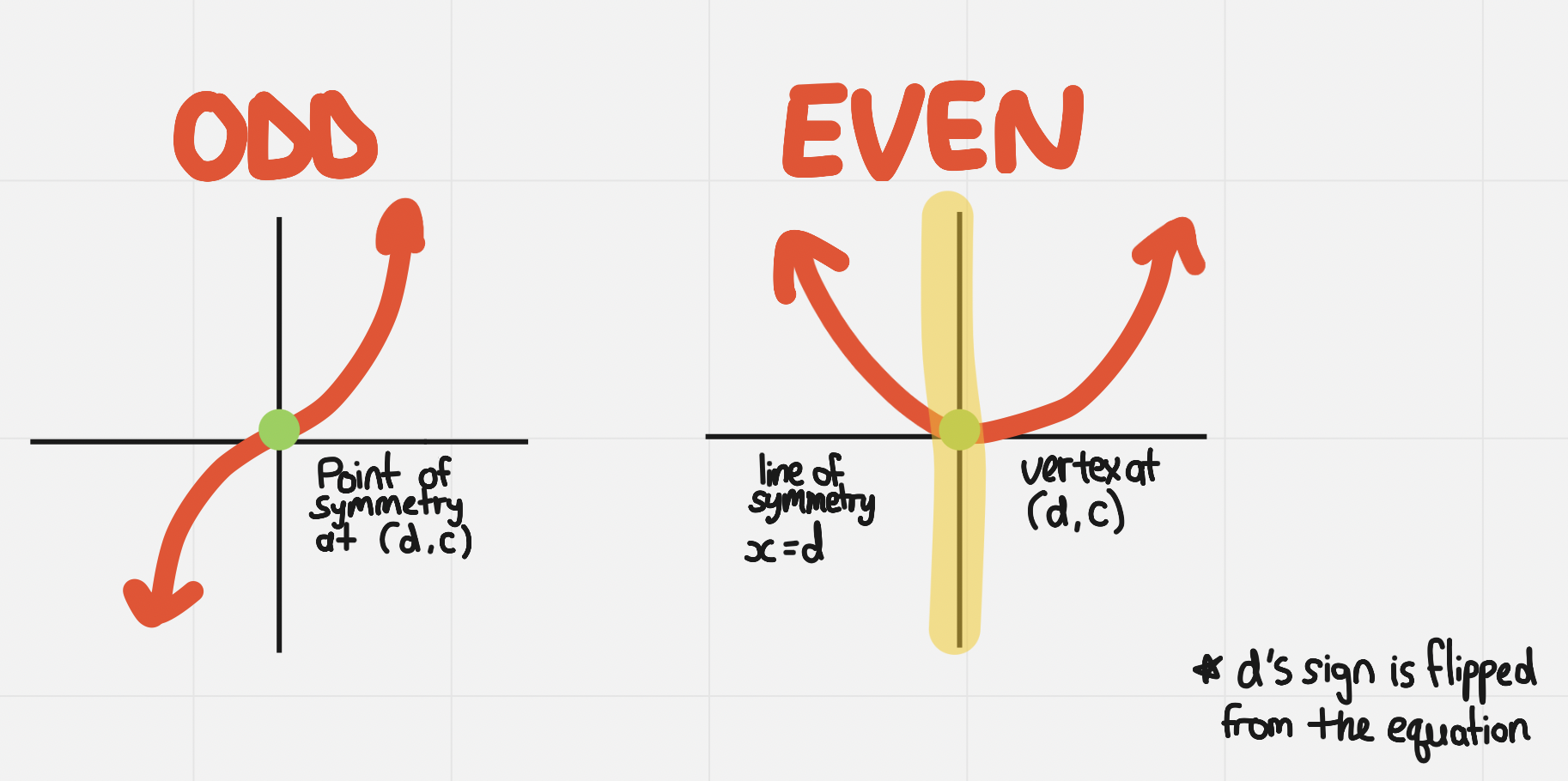
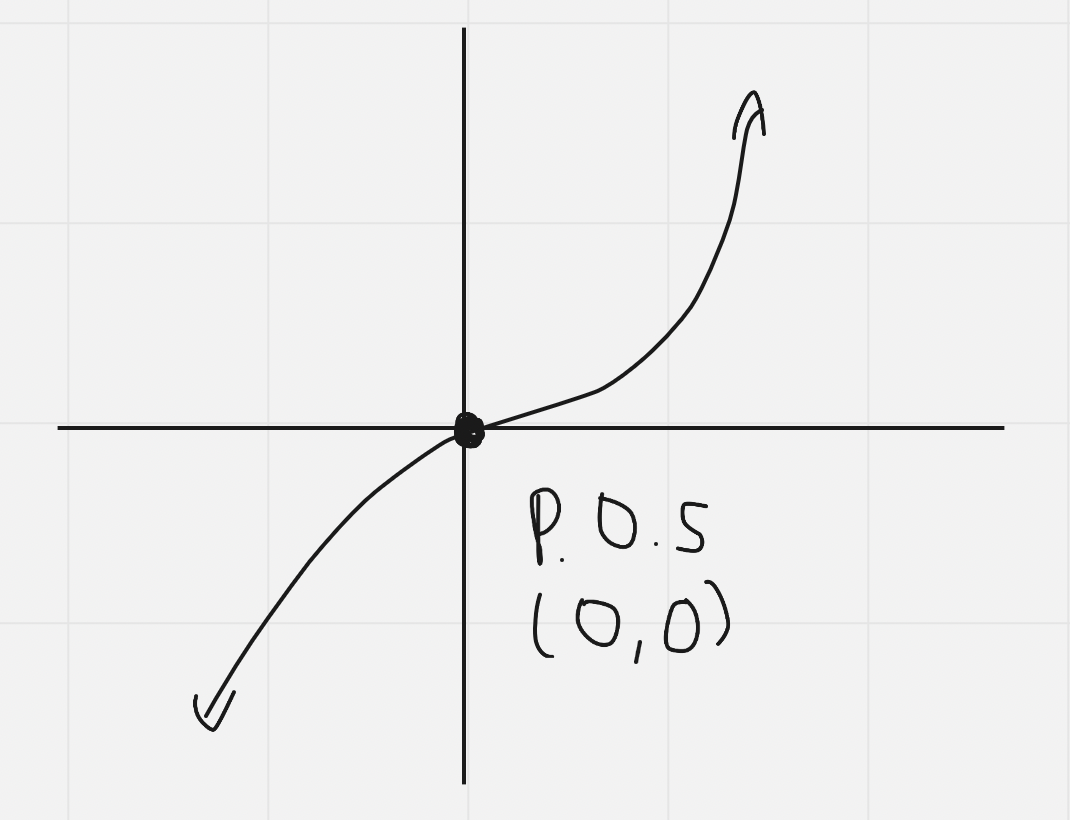
==Odd== degree functions have a ==point of symmetry==
The point of symmetry for ==odd== degree polynomials is ==(0,0)==
- At the point of symmetry, if someone were to take the pieces separated by the point and twist them 180º respectively, they would be the exact same
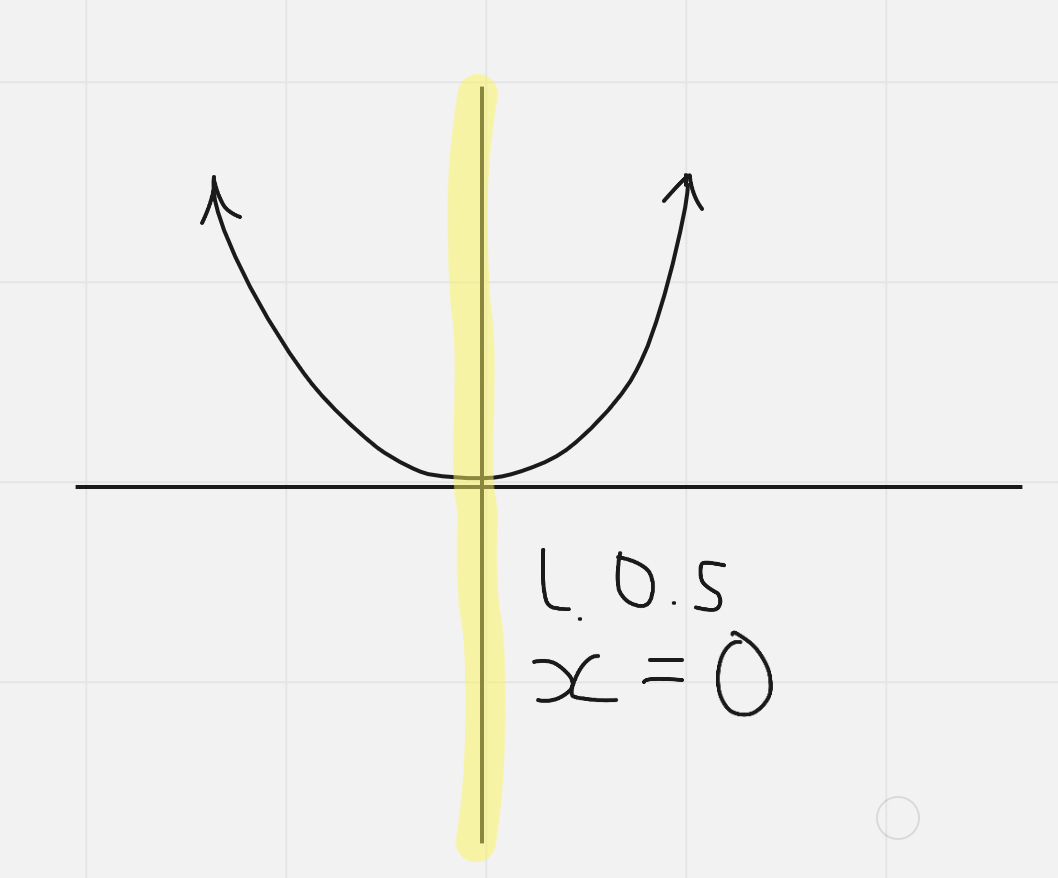
^^Even^^ degree functions have a ^^line of symmetry^^
The line of symmetry for ^^even^^ degree polynomials is ^^x=0^^
- The line of symmetry splits the function in half perfectly evenly
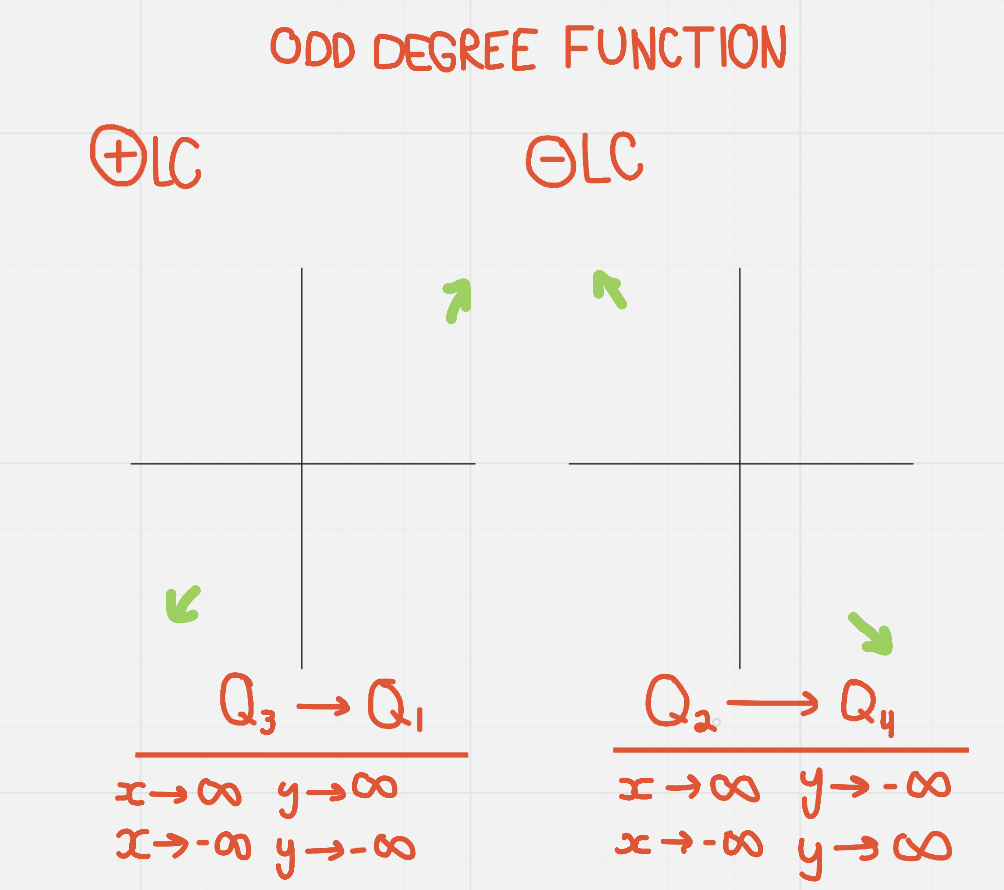
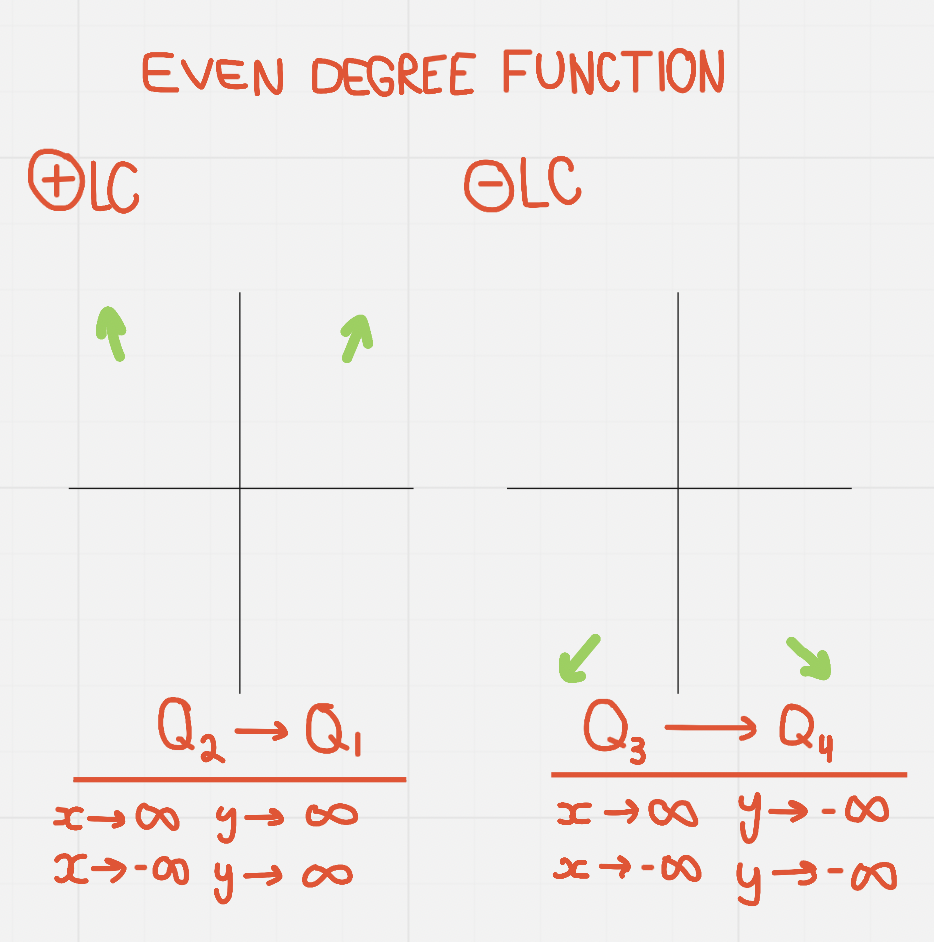
End Behaviour
- End behaviours describe what happens “after the arrow” → they tell us about the drawn ends and where they continue to
For Domain:
 Negative infinity means that our ends are moving left
Negative infinity means that our ends are moving left
Positive infinity means that our ends are moving right
For Range:

Negative infinity means that our ends are moving down
Positive infinity means that our ends are moving up
The leading coefficient also plays a role…..
Assessing End Behaviour From a Graph’s Endpoints
==Odd Degree:==
^^Even Degree:^^
Characteristics of Polynomial Functions
Not for power functions
==Odd Degree Polynomials==
- All min or max points are generally called turning points
==Turning points for odd degree polynomials:==
Odd degree polynomials always have an ==even amount of turning points==
The most number of turning points that you can have is n - 1, where n is your degree
==All odd degree polynomials….==
- Have only a local max or min, with no absolute max or min
- Have at least one x intercept, and at most n x intercepts (where n is the degree)
- May have a point of symmetry
^^Even Degree Polynomials:^^
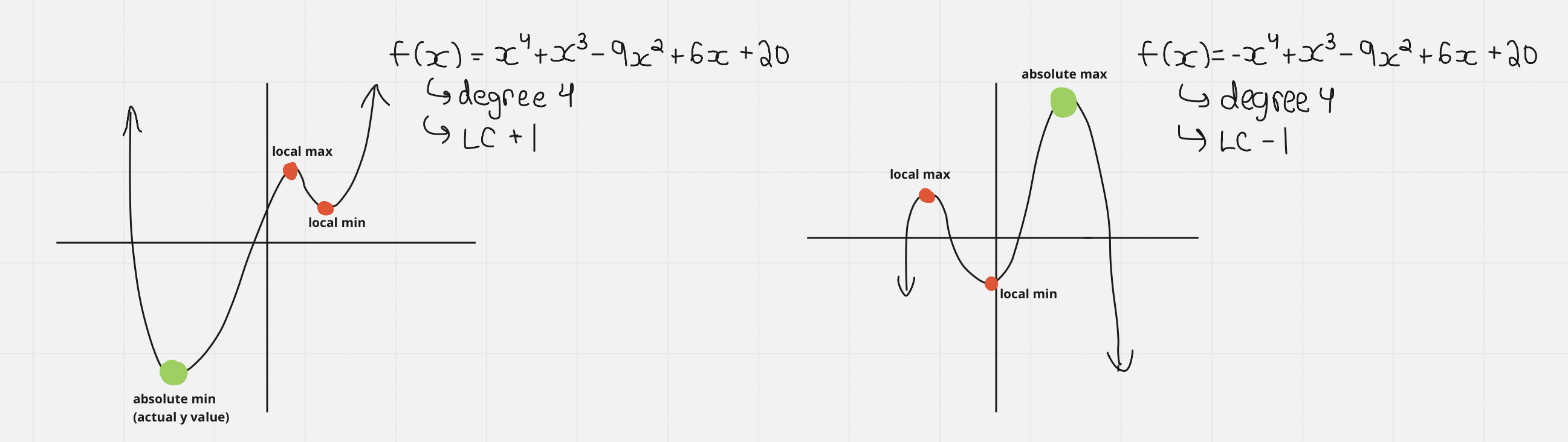
- All max and min points are called turning points
^^Turning points for even degree polynomials:^^
Even degree polynomials always have an ^^odd number of turning points^^
The most number of turning points that you can have is n - 1, where n is your degree
^^All even degree polynomials….^^
- Have an absolute max or min, and can also have local max or min points
- Has a minimum of 0 x intercepts, and a maximum amount of n x intercepts, where n is the degree
- May have a line of symmetry
For both ==odd== and ^^even^^ degree polynomials:
Polynomials function can have at most n -1 turning points
Max TP = n - 1
and from this we get…
n = TP + 1 to find the least possible degree
Finite Differences
For a polynomial function of degree %%n%% (where n is a positive integer), the %%n%%th differences…
- Will be constant
- Has the same sign as the leading coefficient
- i.e. if numbers come out positive, the LC is positive; if numbers come out negative, the LC is negative
- Equal to:
d = a(n!)
where d is the constant difference, a is the leading coefficient, and n! is the degree factorial
- Factorial: a number broken up and multiplied by itself, e.g. 5! = 5 x 4 x 3 x 2 x 1
Equations and Graphs of Polynomial Functions
The graph of a polynomial function can be sketched using…
- Degree
- Leading Coefficient
- Degree and Leading coefficient let us find end behaviour
- x intercepts
- y intercept
When a polynomial is in factored form…
The x intercepts can be found from its factors (roots)
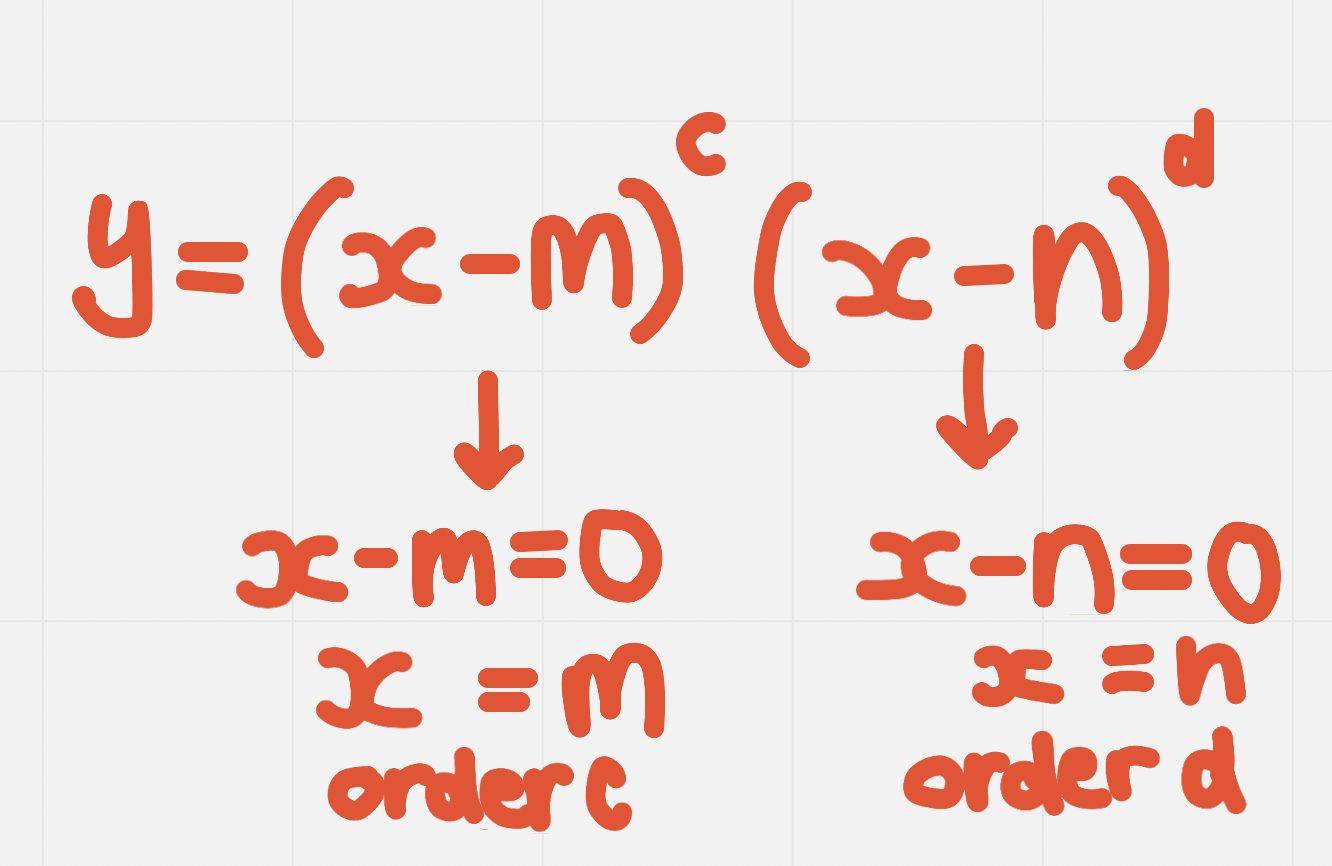
%%Exponents are called orders%%, the order of roots can also be referred to as multiplicity
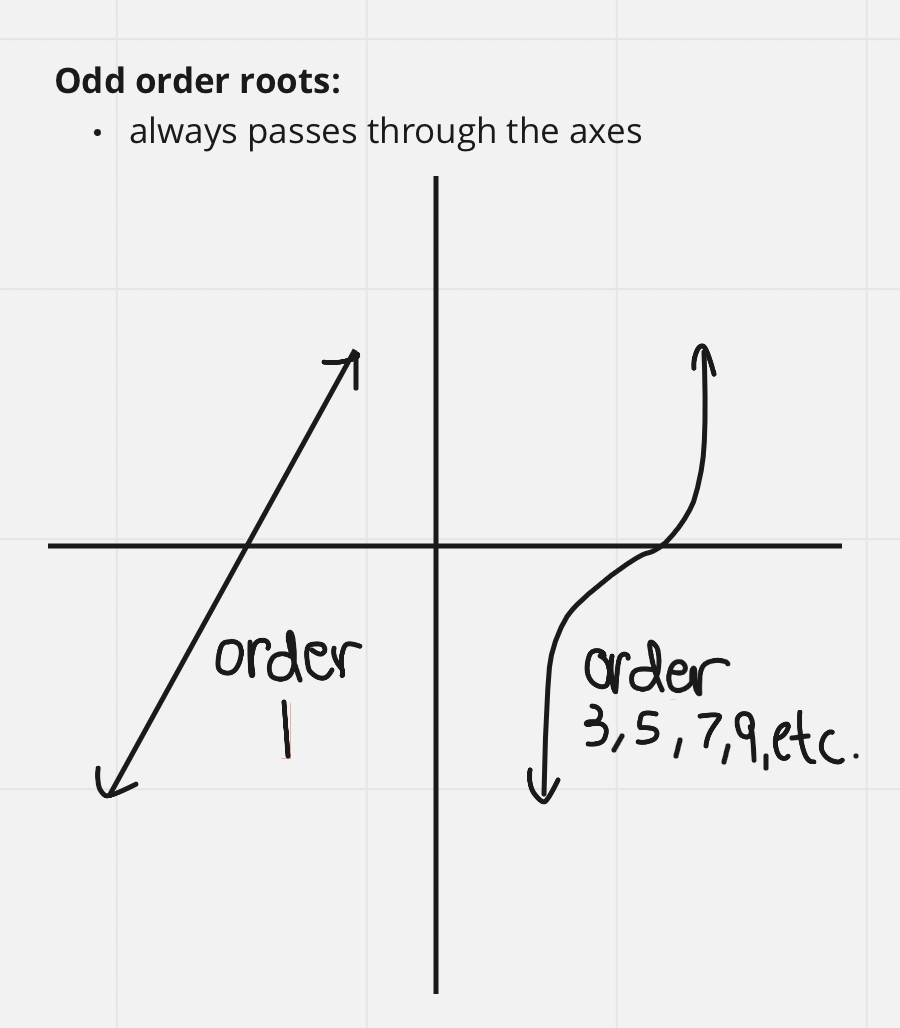
Odd Order Roots
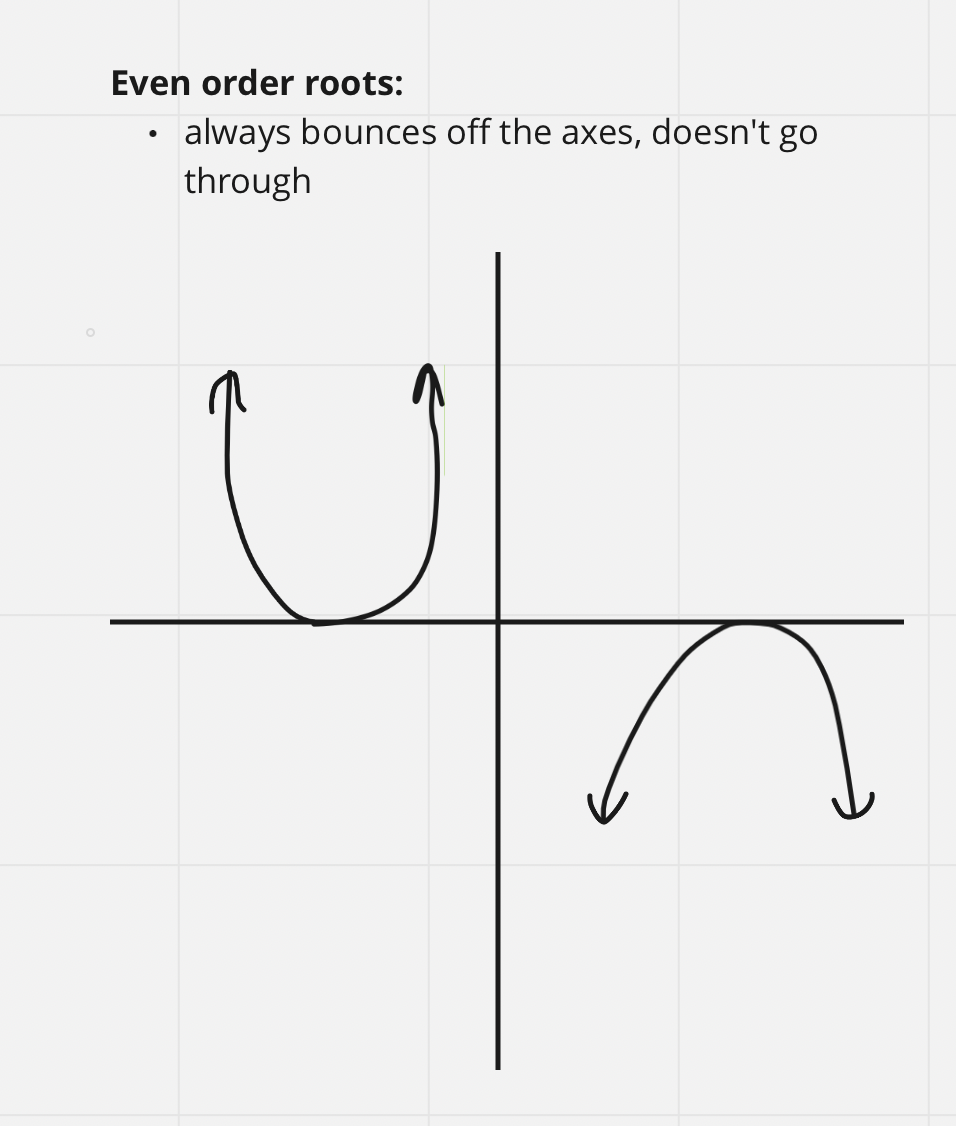
Even Order Roots
Order: Finding and Solving
| a. Degree: add all orders on the roots | b. Leading coefficient: coefficients of roots multiplied, raised to their order | c. End behaviour: look at if it is even or odd degree, and if the LC is positive or negative, then use rules |
|---|---|---|
| d. Roots (x intercept) with order: substitute y=0 and solve for x anywhere that x is in the equation | e. Y intercept: sub x=0 and solve the equation with that substitution | f. Sketch: look at all orders as instructions on how to draw the lines and roots as instructions on where to draw the lines. Depending on whether the order is positive or negative, you will either draw a line that passes through the axes (odd) or one that bounces off of the axes (even) |
g. Positive/Negative Intervals
Positive: when is function above the axis
Negative: when is function below the axis
- Use your sketch to see and create a chart to write your statements
Example:


Transformations of Polynomial Functions
Translations Overview
Be sure to describe translations from left to right

Mapping Notation
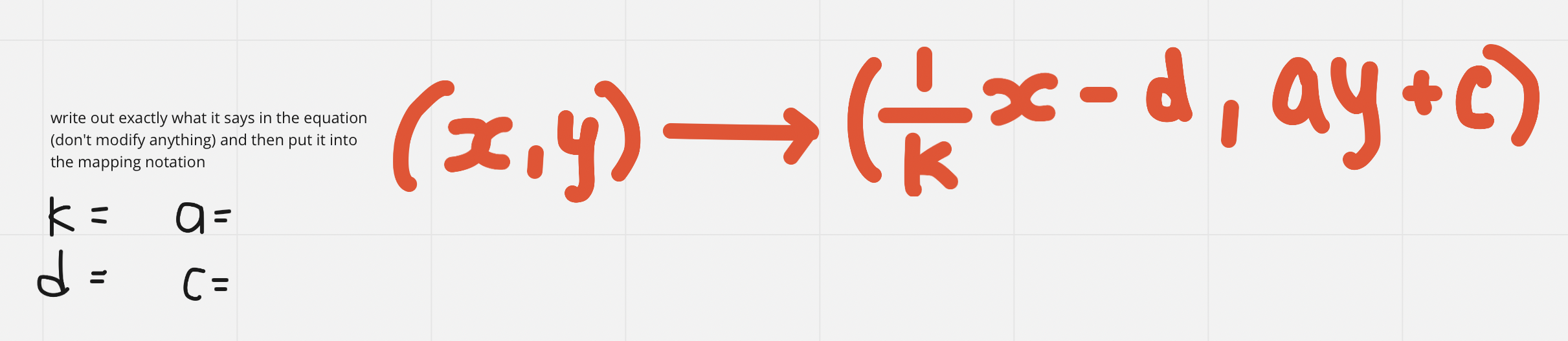
Odd and Even Degree, Find Point or Line of Symmetry
Rates of Change
Rate of change: a measure of the change in one quantity (the dependent variable) with respect to the change in another quantity (the independent variable)
- Something “per” something else
2 Types of Rates of Change
- Average rate of change (AROC): Slope of the secant line on a graph → Rate of change over an interval
- Instantaneous rate of change (IROC): Slope of the tangent line on a graph → Rate of change at a specific instant
Average Rate of Change (AROC)
Slope of the secant line
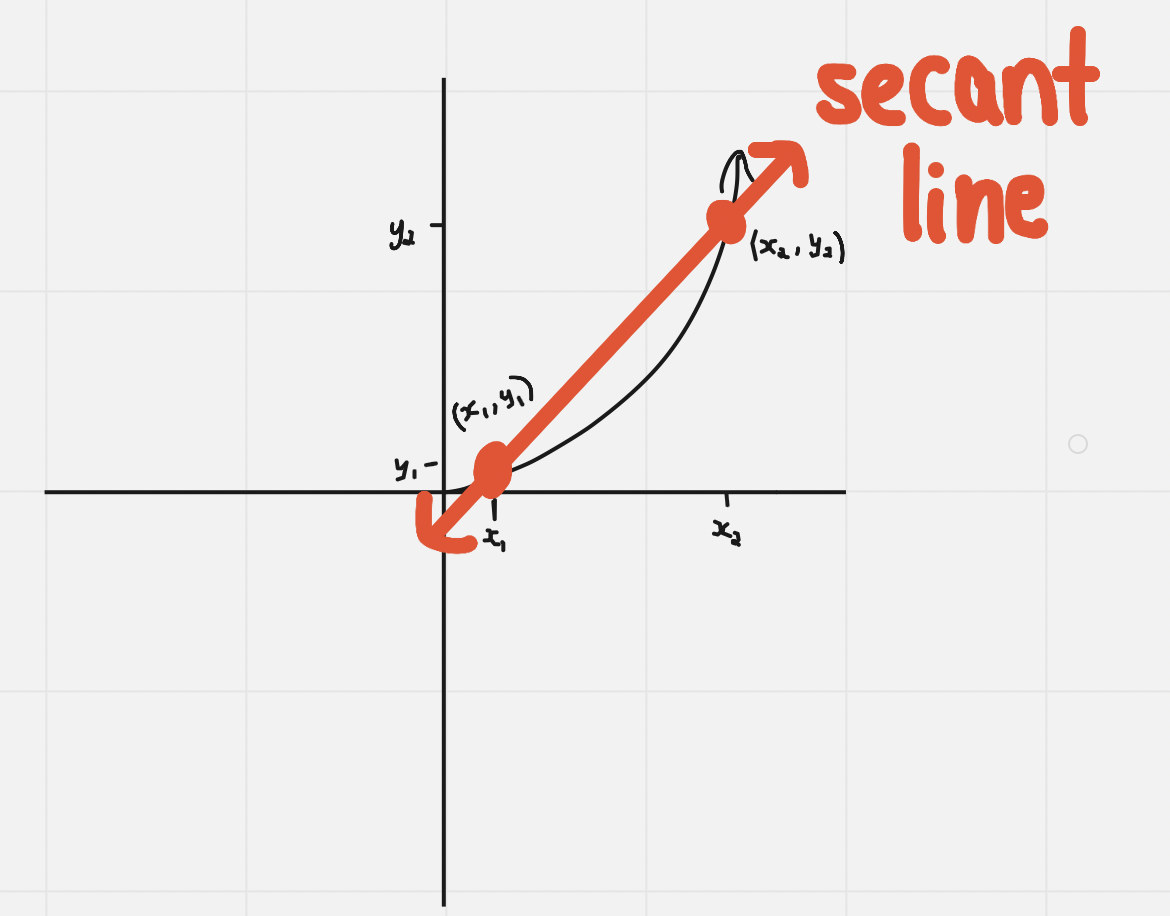
Formula for AROC:
From a graph:
- Graphically: we are looking for the steepness of our lines, that is what matters here - if you see a straight line, it is AROC of 0 (you can tell just by looking at it)
From a table of values:
- Generate points by combining x and y sections in table of value to be (x,y) coordinates
Instantaneous Rate of Change (IROC)
Change at an instant
We can determine the approximate value for IROC at a given point when given a…
Graph: Slope of a tangent line
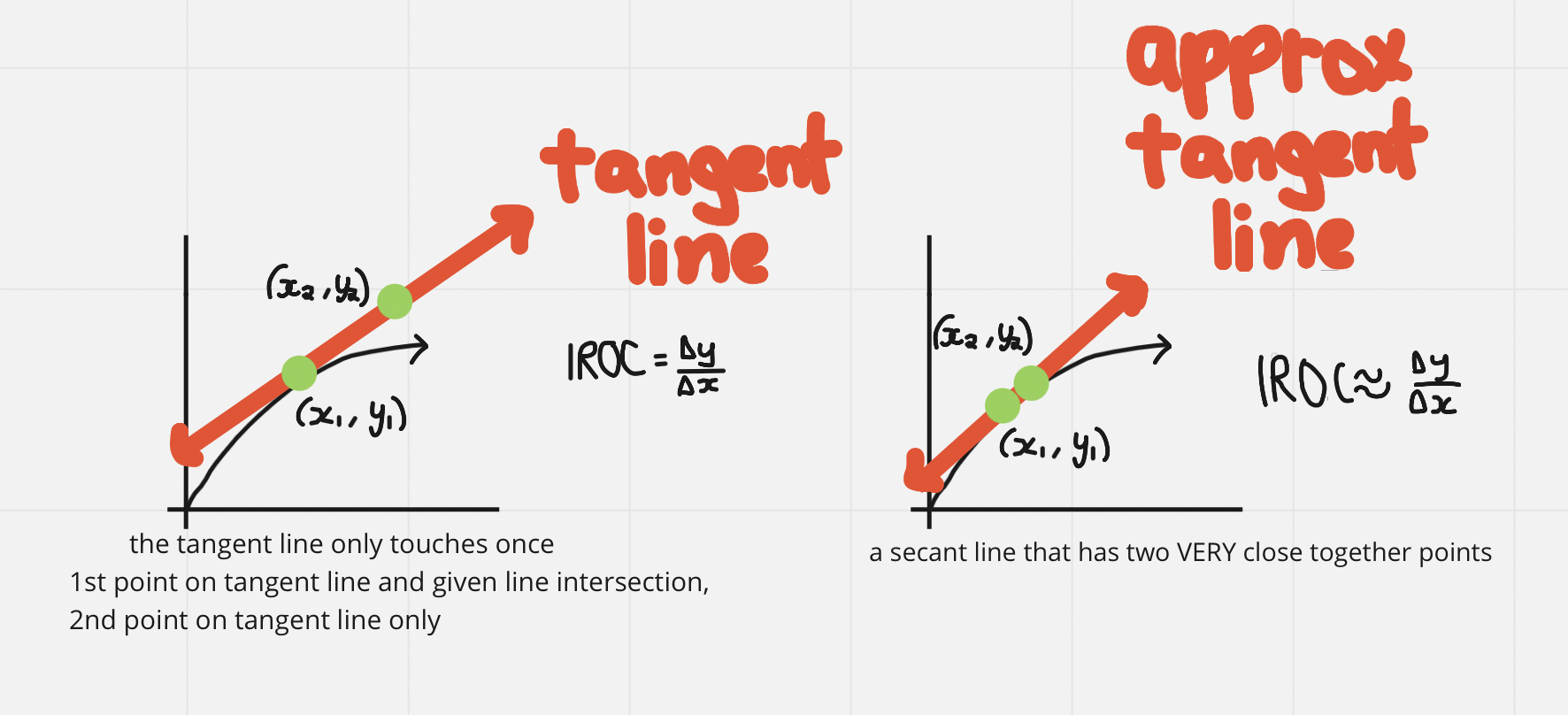
Table of Values
- Use the point right before and right after to create a secant line with 2 very close together points
Equation
- The closer your 2 endpoints are, the better your approximation of IROC
To estimate IROC at a given x value from an equation, add or subtract 0.001 to the x value and find your AROC
With negative numbers:
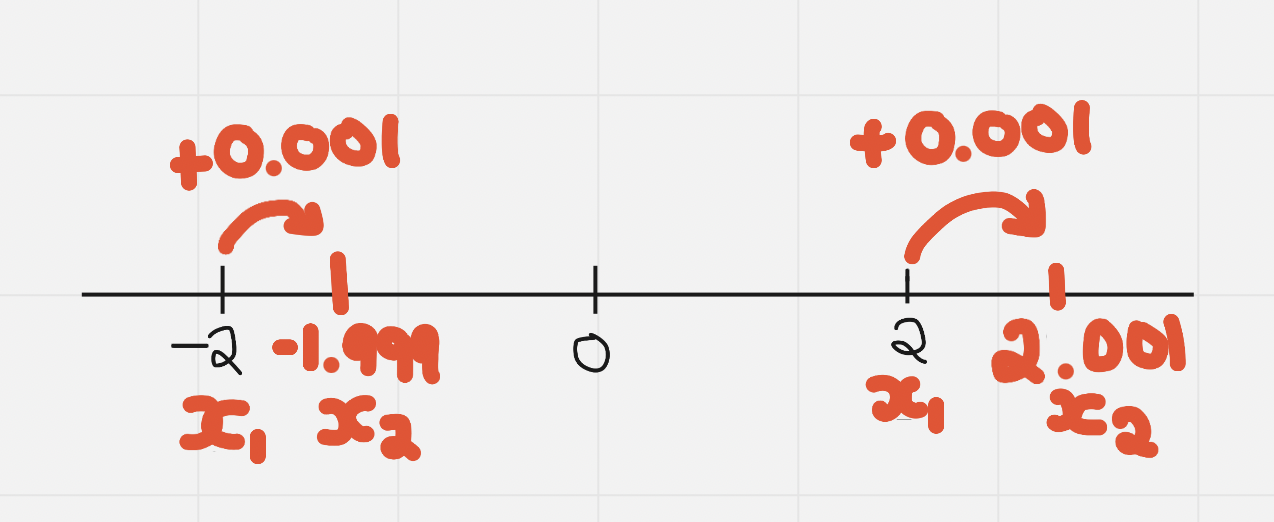
- Keep all decimals in your process
Odd Functions vs. Even Functions
Odd or even functions, NOT odd or even degree functions
Odd Functions:
- Graph: Have a point of symmetry at (0,0)
- Algebraic Proof: Satisfies the property
-f(x) = f(-x)
- Polynomial Equation: All exponents are odd in expanded form and there are no constants
Even Functions
- Graph: Line of symmetry at x=0
- Algebraic Proof: Satisfies the property
f(x) = f(-x)
- Polynomial Equation: If all exponents are even in expanded form, there may be constants
- Constants are really x⁰ and 0 is even