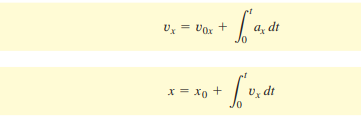Chapter 2: Motion along a Straight Line
Average velocity during a particular time interval for a particle is a vector quantity whose x-component is the change in x divided by the time interval.
The x-component of average velocity, or average x-velocity, is the x component of displacement,Δx, divided by the time interval,Δt, during which the displacement occurs.
The rule for the sign of velocity depends on four main case scenarios:

- For example, let’s say that a particle is at point 19 m from the origin after 1s of moving, and 4.0 s after the start it is at point 277 m from the origin.
- The x-component of the displacement is the change in the value of x (277 m - 19 m) = 258 m, that took place during the time interval of (4s-1s)=3s.
- We define the particle’s average velocity during this time interval as: (258m)/(3s)=86 m/s.
The velocity at a specific instant of time or specific point along the path is known as instantaneous velocity.
==In the language of calculus, the limit of Δx/Δt as Δt approaches zero is called the derivative of x with respect to t and is written dx/dt.==
- The instantaneous velocity is the limit of the average velocity as the time interval approaches zero.
- It equals the instantaneous rate of change of position with time.

On a graph of position as a function of time for straight line motion, the instantaneous x-velocity at any point is equal to the slope of the tangent to the curve at that point.
- If the tangent to the x-t curve slopes upward to the right, then its slope is positive, the x-velocity is positive, and the motion is in the positive x-direction.
- If the tangent slopes downward to the right, the slope of the x-t graph and the x-velocity are negative, and the motion is in the negative x-direction.
- When the tangent is horizontal, the slope and the x-velocity are zero.
A motion diagram shows the particle’s position at various instants as well as arrows to represent the particle’s velocity at each instant.
The change in the x-component of velocity Δv(x), divided by the time interval Δt is known as average acceleration.
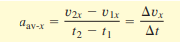
The instantaneous acceleration is the limit of the average acceleration as the time interval approaches zero. In the language of calculus, instantaneous acceleration equals the derivative of velocity with time.
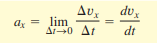
The rules for the sign of the acceleration are:

On a graph of x-velocity as a function of time, ==the instantaneous x-acceleration at any point is equal to the slope of the tangent to the curve at that point==.
Tangents drawn at different points along the curve have different slopes, so the instantaneous x-acceleration varies with time.
The second derivative of any function is directly related to the concavity or curvature of the graph of that function.
Here, the acceleration is the double derivative of dx/dt.
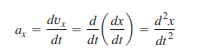
Where the x-t graph is concave up (curved upward), the x-acceleration is positive and is increasing.
At a point where the x-t graph is concave down (curved downward), the x-acceleration is negative and is decreasing.
At a point where the x-t graph has no curvature, such as an inflection point, the x-acceleration is zero and the velocity is not changing.
The three equations for motion in a straight line and in constant acceleration are:
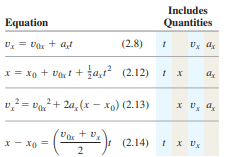
Here the vx is the final velocity, v0x is the initial velocity, ax is the acceleration, t is the time, x is the final position and x0 is the starting position.
Free fall is a case of motion with constant acceleration.
- The magnitude of the acceleration due to gravity is a positive quantity, g.
- The acceleration of a body in free fall is always downward.
- ==Here, g=9.8 m/s2.==
When the acceleration is variable(not constant), ==we have to integrate the acceleration at each point in the distance==. Thus the equations become: