Geometry 1 | Theorems, Postulates, Definitions and Formulas

Theorems

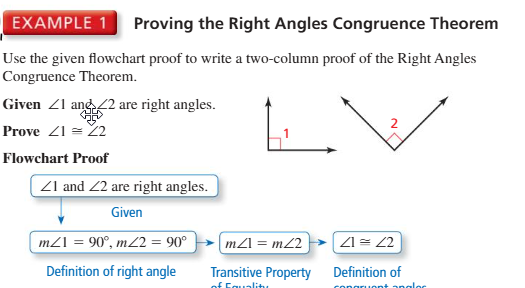
Right Angles Congruence Theorem (2.3)

Metadata:Textbook pg 106.

This theorem says that all right angles are congruent.

Example

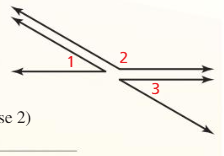
Congruent Supplements Theorem (2.4)

Metadata: Textbook pg. 107

If two angles are supplementary to the same angle, then the two angles are congruent to each other. This theorem is often used in proofs to establish relationships between angles in geometric figures, particularly in triangle and polygon contexts.

Imagine it like this:

• You just need to know if it’s supplementary. Then you can solve for the whole thing.

• Either know the angle of the congruent one

  • If its algebra get X and fill it in. and solve. Set it equal to each other! Congruent means they’re equal.

• Depending if it’s supplementary or complementary (read the problem) subtract your angle from 180 or 90. That’s how much that angle is.

Example

Congruent Complements Theorem (2.5)

Same as 2.4, but adds up to 90

Postulates

Ruler Postulate (1.1)

Metadata: Textbook pg 12, Lesson 1.2.

The points on a that can be matched one to one with real numbers. The real number assigned to a point is the coordinate of that point. Every segment has a length that can be calculated as the absolute difference between the coordinates of its endpoints.

This lets us measure lengths in geometry.

Example:

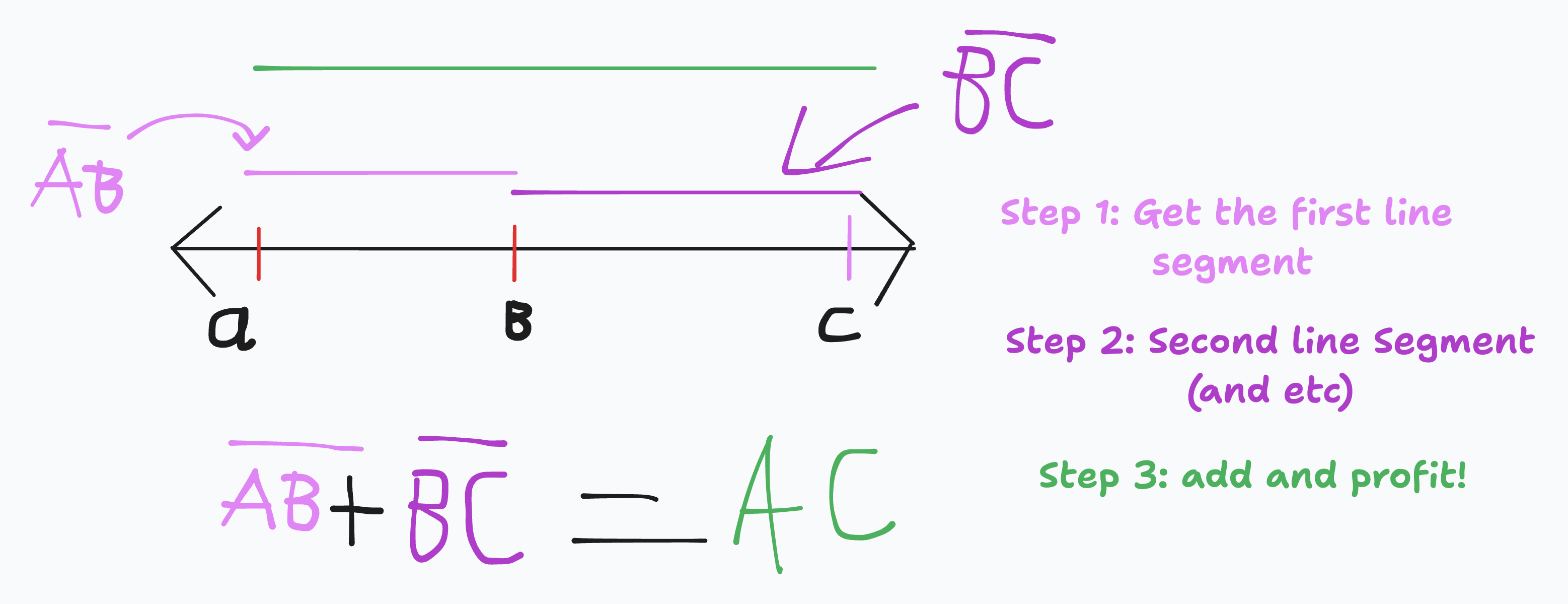
Segment Addition Postulate (1.2)

Metadata: Textbook pg.13

This lets you say that if point B lies on segment AC, then the length of AB plus the length of BC equals the length of AC.

Example

Protractor Postulate (1.3)

• The Protractor Postulate states that you can measure angles in degrees, where the measure of an angle is the absolute value of the difference of the real numbers matched with the rays.

TLDR: basically it gives angles a number (like ruler postulate) and let’s us do things to them once we know their numbers.

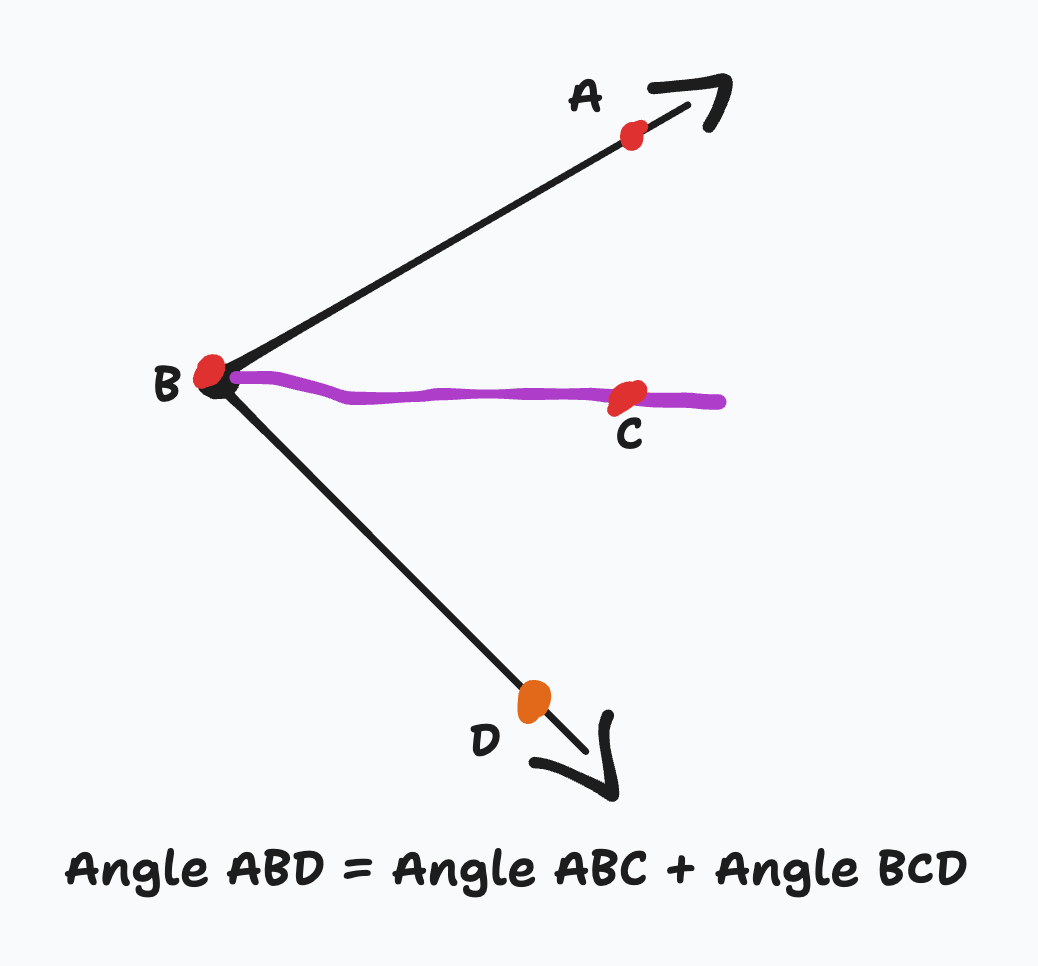
Angle Addition Postulate (1.4)

Think about this like the Segment Addition Postulate.

Example

Definitions

Types of Angles

Formulas

Distance Formula

Metadata: Textbook pg 14

2D Distances

d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Example

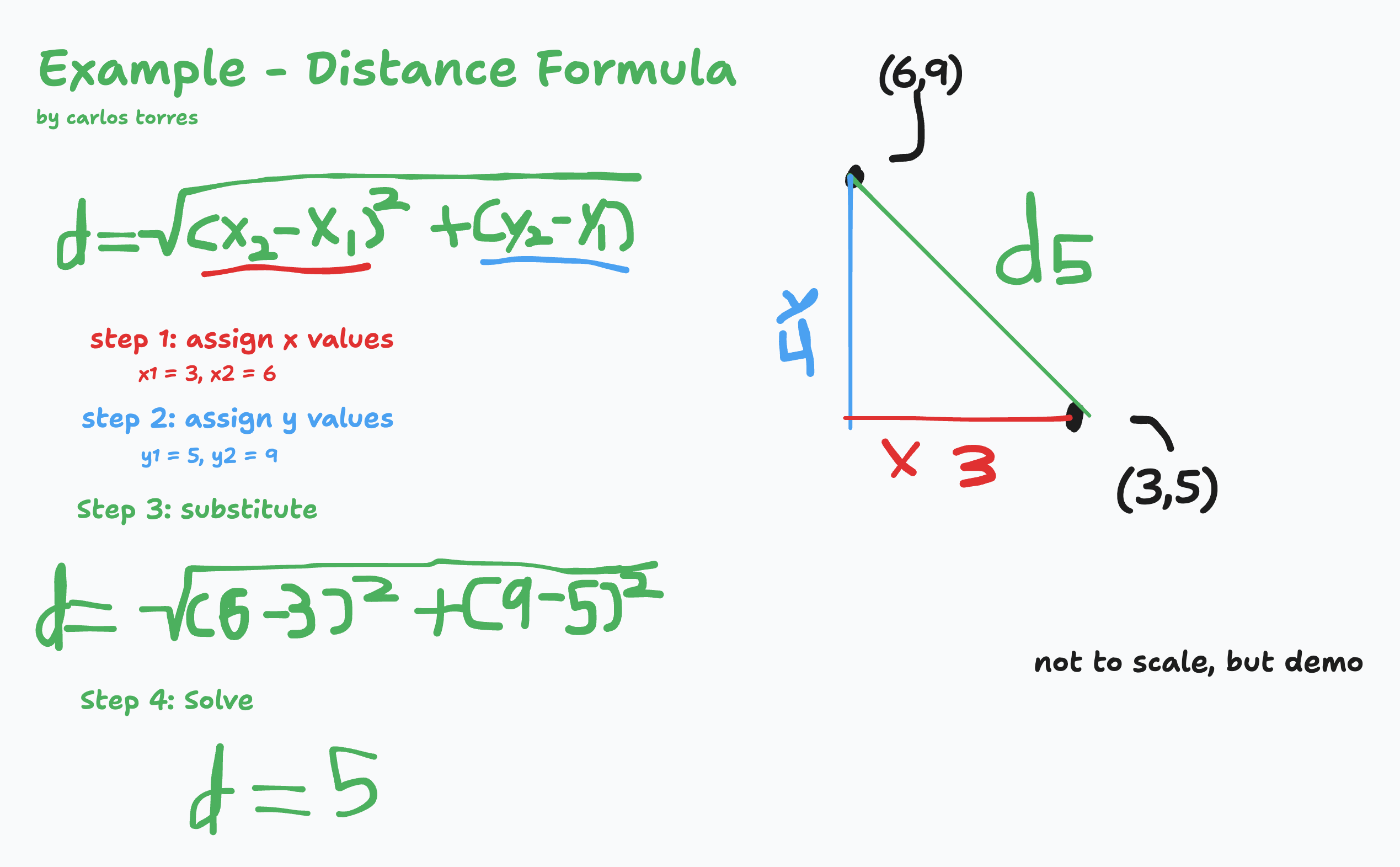
Note: Remember the Pythagorean Theorem? Whenever you use the distance formula, you’re calculating the hypotenuse of a right triangle, where the differences in x and y coordinates represent the two legs.

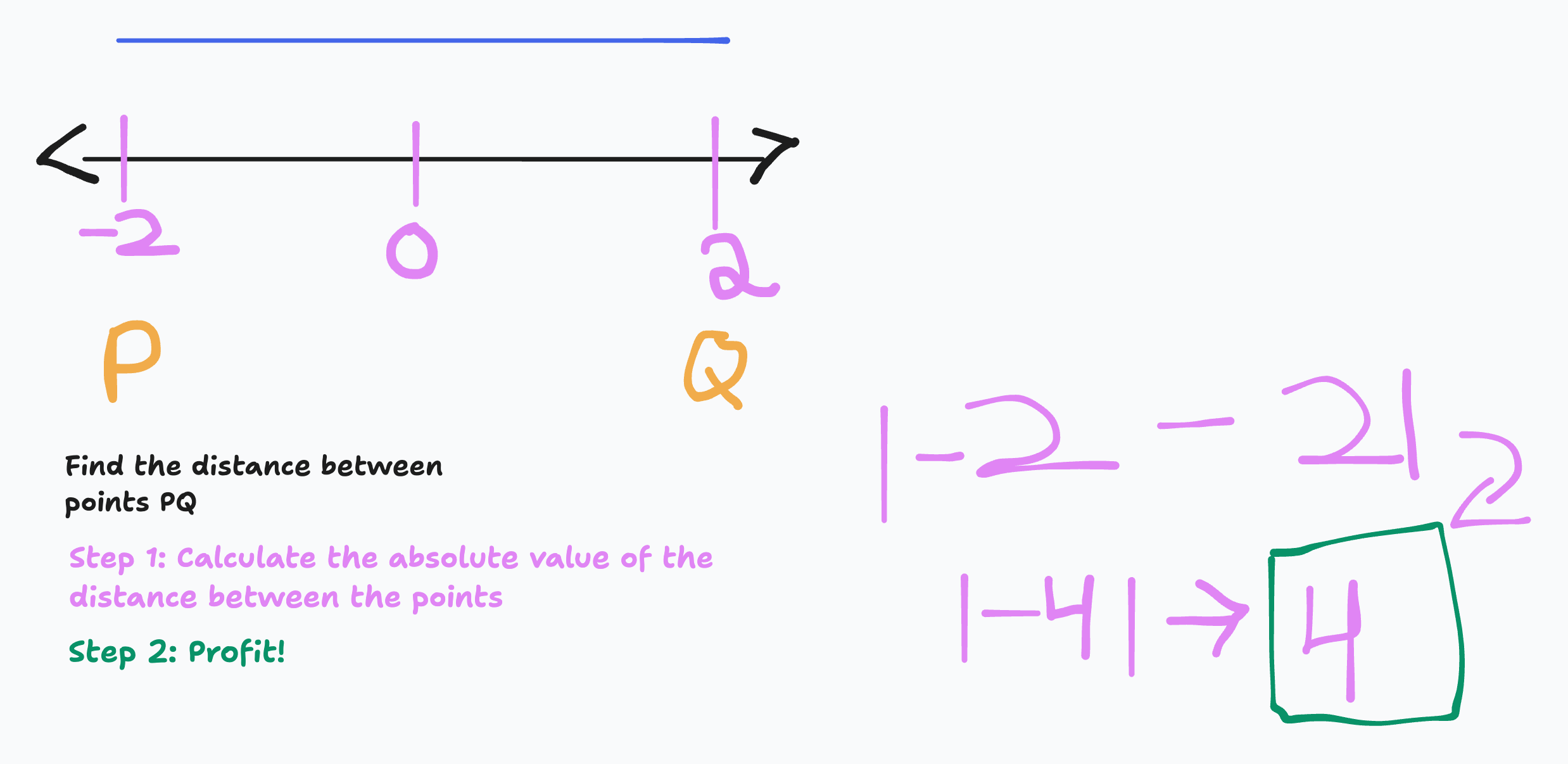
1D Distances

d=|x_1-x_2|

Example

Partitioning a Line Segment to A Ratio

Metadata: pg 22.

x=\frac{ax_1+bx_2}{a+b}

This formats the partition segment to the ratio b:a.

Example - Partitioning

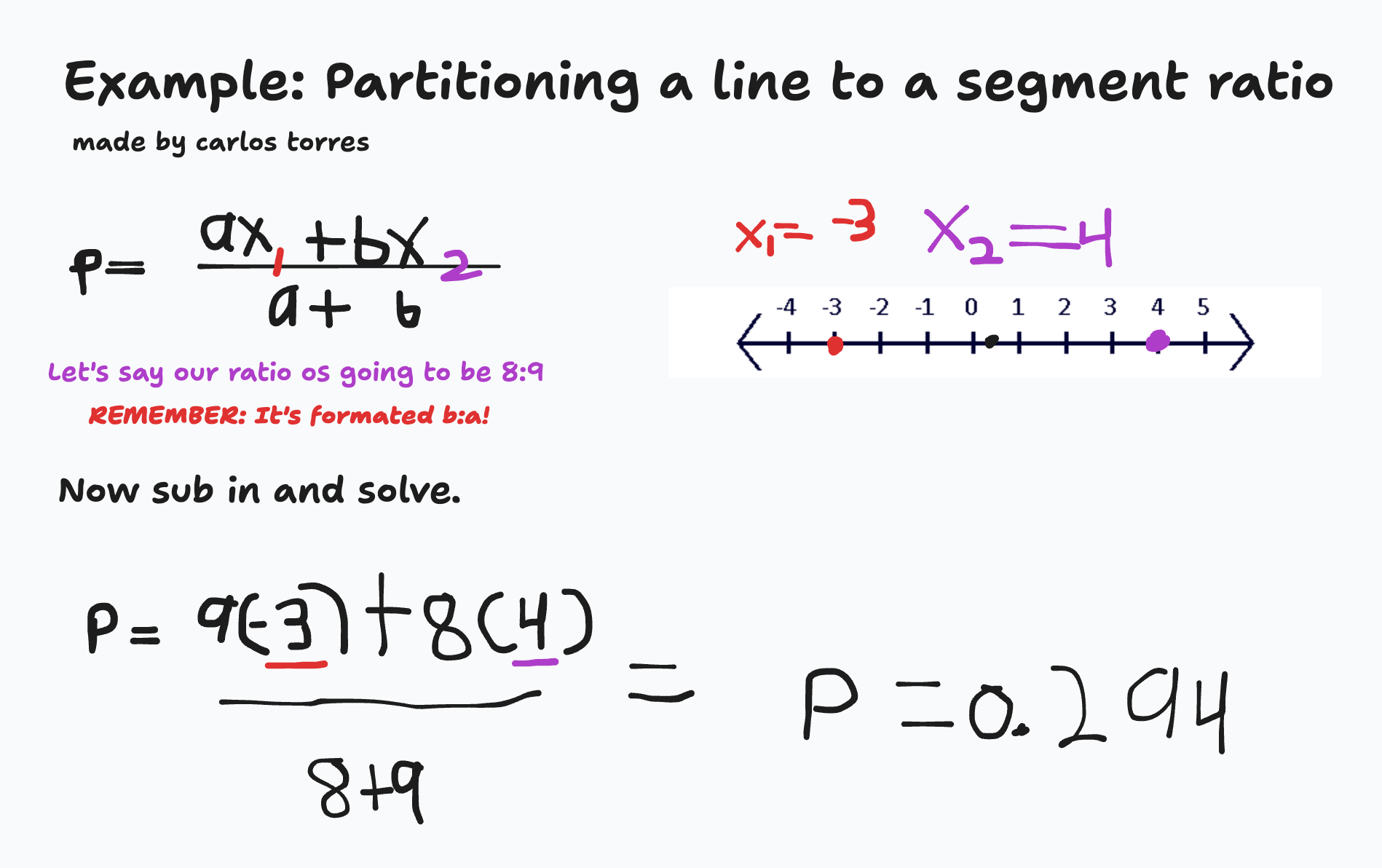
Example - Finding a midpoint

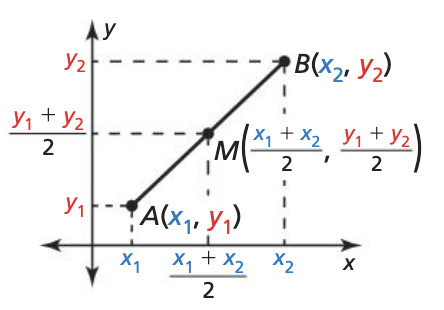
Midpoint of a Segment in a Coordinate Plane

Metadata: pg 23

This formula allows you to find the middle point of a segment, but on graphs. It work’s very similar to finding a midpoint on a numberline. See “Partitioning a Line Segment to A Ratio” example to get an idea.

\left( \frac{x_1 + x_2}{2},\ \frac{y_1 + y_2}{2} \right)

Example