Forms of a Quadratic Function

• Standard Form; y=ax^2+bx+c

• Vertex Form; y=a(x-h)^2+k

• Intercept/Factored Form; y=a(x-p)(x-q)

Quadratics on a Graph

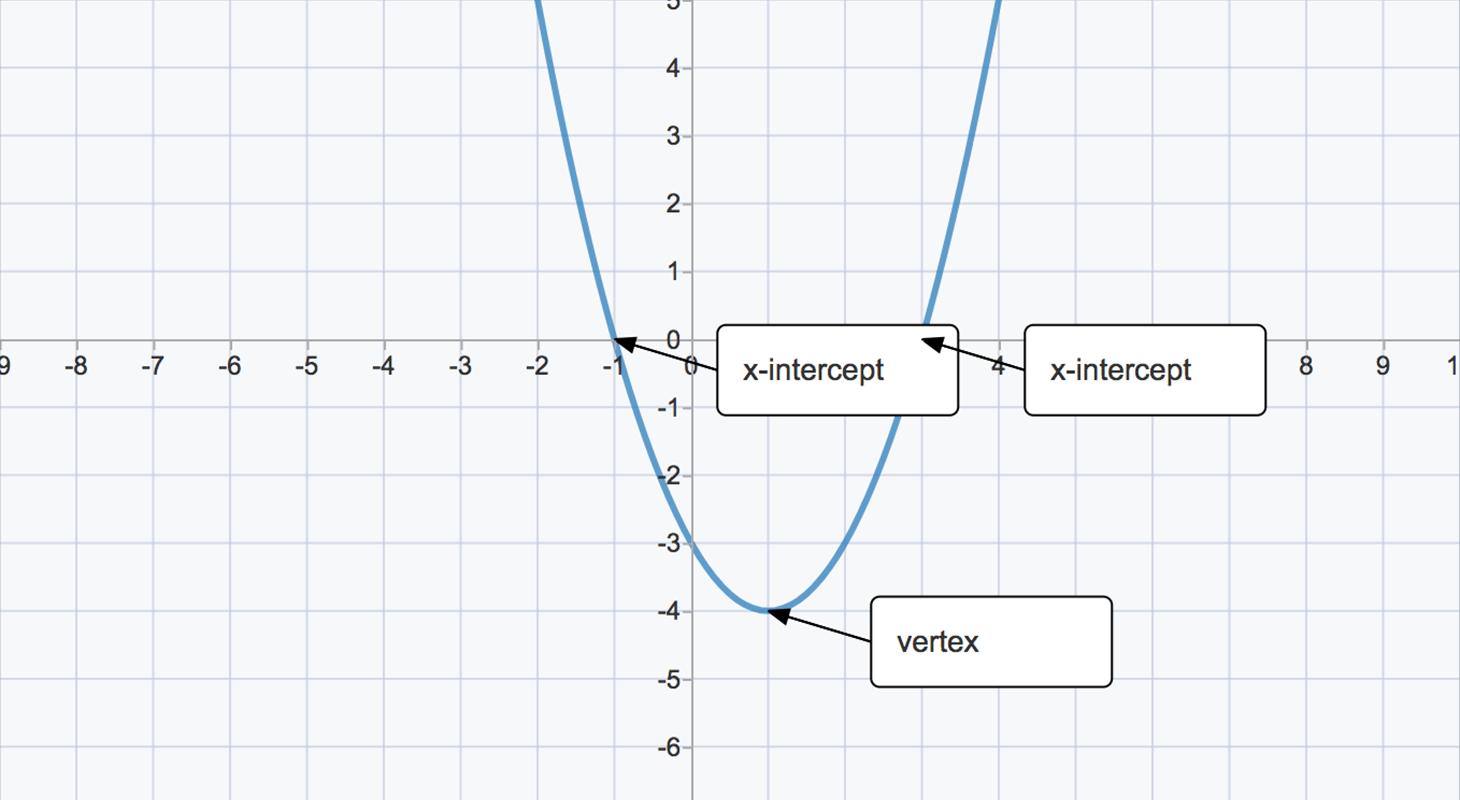
Quadratics are ALWAYS parabolas when graphed. Unlike linear equations and inequalities, quadratics have two x-intercepts, also referred to as zeros. The tip of the parabola is the vertex, which represents a minimum or a maximum. The y-coordinate of the vertex is synonymous to the max/min, regardless of the form.

Finding Vertexes

Standard Form

• x=-b/2a then plug into the equation y=ax^2+bx+c

Vertex Form

• vertex=(h,k)

Intercept Form

• find average p and q to find x, and then plug x into equation to find y

Determining Maximum and Minimum

• ex. y= -2x^2+8x+7

  • a=-2 b=8 c=7

  • since a is < 0, you’re going to have a maximum point

  • if a > 0, you have a minimum

Zeros

Zeros and x-intercepts are synonymous (they’re the same). They’re called zeros because they are the x-values that make y/f(x) equal zero.

Finding Zeros From Intercept Form

Finding zeros from intercept form is very simple! All you need to do is take the opposite value of the number or variable after x. For example, if y=a(x-6)(x+5), then its zeros are 6 and -5.

• Intercept form; a(x-p__)(x-q)__

Finding Zeros From Standard Form (Conversion)

In order to find zeros from standard form without a graph, you’ll have to convert to Intercept form. Here are the steps to do that.

• Ex. 8x^2-4x=40

  • Rearrange equation into standard form; 8x^2-4x-40=0

  • Factor out anything common to all terms; 4(2x^2-x-10)=0

  • Factor the trinomial; 4(2x-5)(x+2)=0

Finding Zeros From Vertex Form

In order to find the zeros, simply set y/f(x) equal to zero and solve for x.

• ex. f(x)=1/2(x-2)^2-8

  • 0=1/2(x-2)^2-8

  • 8=1/2(x-2) > 16=(x-2)^2 > √16=√(x-2)

  • 4=x-2 and -4=x-2 (remember, when square rooting a variable, you must account for both the positive and negative outcomes)

  • x= 6 and x=-2

Zero Product Property

If two factors multiply and result in a zero, then at least one of those things must be equal to zero. For example, if (ax-m)(bx-n)=0, then either (ax-m)=0 and (bx-n)=0. This property is very useful to have in your back pocket especially in case when you aren’t given C.

Finding Zeros When Missing C (Standard Form)

• ex. 3x^2-6x

  • 3x^2-6x=0

  • 3x(x-2)

  • 3x=0 > x=0

  • x-2=0 > x=2

Finding Zeros When Missing B (Standard Form)

• ex. 100-121a^2=0

  • 121a^2=100

  • √a^2=√100/121

  • a=+/- 10/11 (when square rooting, add +/- for both solutions)

Finding Zeros W/ the Quadratic Formula

If I’m being honest, using the quadratic formula could use up a lot of your time compared to the other tactics, but, if you find yourself to be more comfortable using the quadratic formula, then do whatever you think will get you a better score.

• The Quadratic Formula: -b+/-√b^2-4a/2a

• Ex. x^2+1=6x

  • x^2-6x+1=0 a=1 b=-6 c=1

  • x= -(-6) +/- √(-6)^2-4(1)(1)/2(1)

  • x= 6+/- √36-4/2 > 6+/-√32/2 > 3+/-4√2/2 > 3+/-2√2

Zeros and Factors

Getting Zeros From Factors

In order to find the zeros of a factor, the Zero Product Property is exactly what you need. It’s as simple as setting the factor to zero and solving the algebraic equation.

Getting Factors From Zeros

All you need to do is solve the equation in reverse by moving all numbers and variable to the same side. So if you have x=3/2, multiple both sides by 2, and then mover the three, which will give you the factor 2x-3.

Factoring Differences of Squares

• ex. 8x^2-18

  • 2(4x^2-9)

  • 2(2x+3)(2x-3)

Factoring Differences of Squares w/ Imperfect Squares

While this isn’t as common on the SAT, it could still be useful to know this info and practice, especially if you’re aiming for a score 1400 and up.

• ex. 27x^2-3k

  • 3(9x^2-k) > 3(3x+√k)(3x-√k)

  • Remember, a square root times a square root is a normal number (so √2 times √2 is equal to 2)

Discriminants

When it comes to parabolas, not all have two x-intercepts, in fact, some don’t have any at all. In order to determine what scenario this without a graph present, all you need to do is calculate the discriminant, otherwise known as b^2-4ac. If the discriminant is…

• Greater than 0; 2 zeros/x-ints

• Equal to 0; 1 zero/x-int

• Less than 0; no zeros/x-ints

Translation

Translation is the sliding/shifting of every point of a figure the same distance and direction. Its orientation, side lengths, and angles stay the exact same.

• Adding/Subtracting From Function

  • (x-n) + k; up k units

  • (x-n) - k; down k units

• Adding/Subtracting from X

  • (x+h); left h units

  • (x-h); right h units

  • I know this doesn’t make much sense logically, so I would recommend memorizing this before the test so you don’t get confused

(I will go in depth into how functions change in the Functions and Graphs Section of the Math Prep)