1. Naturaleza del análisis de regresión - Econometría Gujarati

• Regresión: estudio de la dependencia de una variable (variable dependiente) respecto de una o más variables (variables explicativas) con el objetivo de predecir la media poblacional de la primera en términos de los valores conocidos o fijos (en muestras repetidas) de las segundas.

  • Históricamente, Francis Galton estudió cómo las estaturas de las personas "regresaban" a la estatura promedio.

• Diagrama de regresión, con recta de regresión

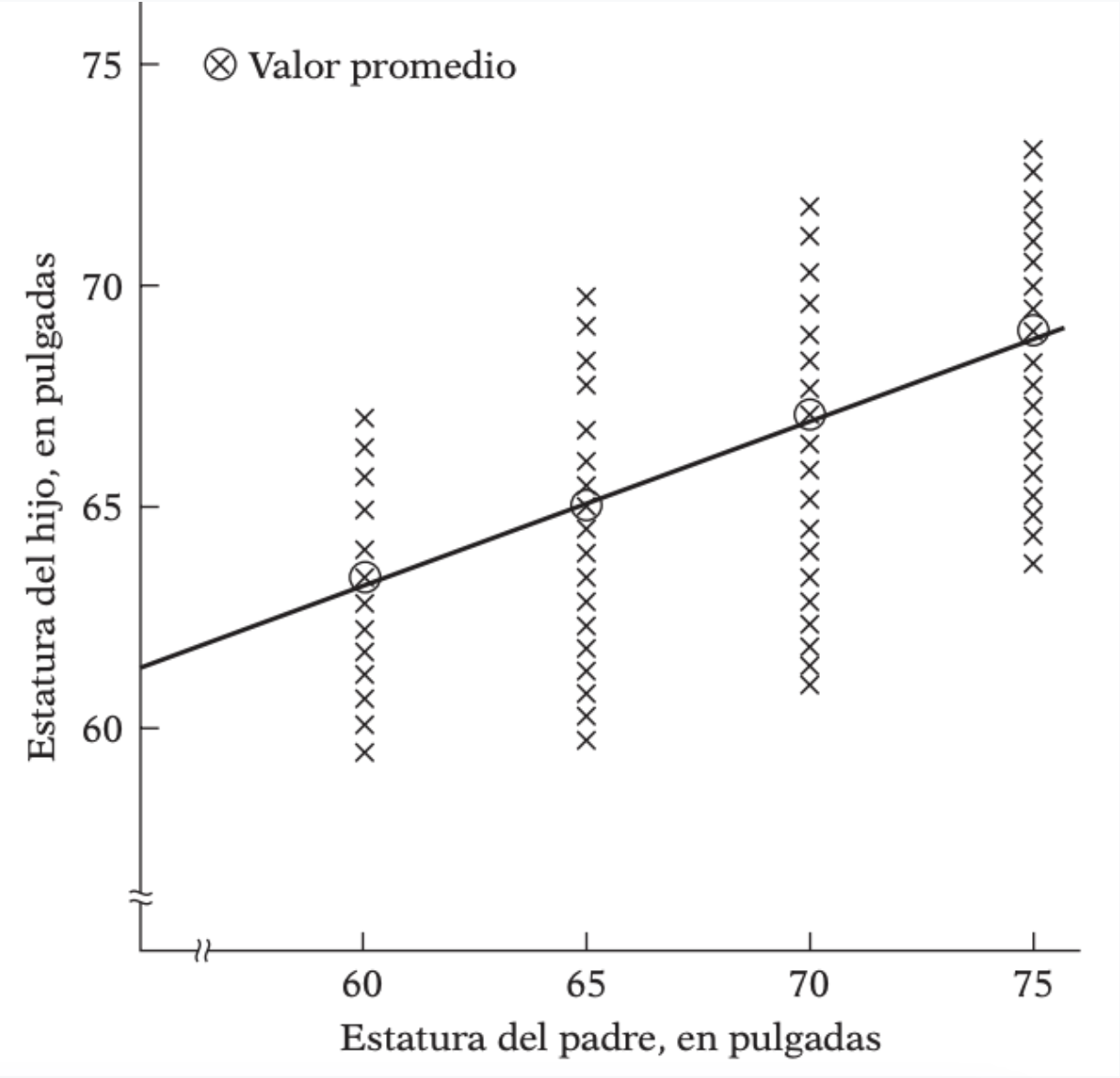
Relaciones estadísticas y relaciones deterministas

• En las relaciones estadísticas entre variables, se analizan variables aleatorias o estocásticas, es decir, con distribuciones de probabilidad.

• Los fenómenos deterministas implican relaciones como la ley de gravedad de Newton.

  • No nos interesan por ahora las relaciones deterministas.

Regresión y causalidad

• A pesar de que el análisis de regresión tiene que ver con la dependencia de una variable respecto de otras variables, esto no implica causalidad necesariamente.

Regresión y correlación

• En el análisis de correlación, el objetivo principal es medir la fuerza o el grado de asociación lineal entre dos variables.

  • Se relaciona estrechamente con la regresión, pero no son lo mismo.

  • El coeficiente de correlación mide esta fuerza de asociación.

• En el análisis de regresión hay una asimetría en el tratamiento a las variables dependientes y explicativas.

  • Se supone que la variable dependiente tiene una distribución de probabilidad. Se asume que las variables explicativas tienen valores fijos (en muestras repetidas).

  • En el análisis de correlación se tratan dos variables cualesquiera en forma simétrica; no hay distinción entre las variables dependiente y explicativa.

Terminología y notación

• Un análisis de regresión simple sólo tiene una variable explicativa.

  • Un análisis de regresión múltiple hay más de una variable explicativa.

• Aleatorio es sinónimo de estocástico: la variable que toma cualquier conjunto de valores, positivos o negativos, con una probabilidad dada.

• La letra Y representa la variable dependiente, y las X representan las variables explicativas.

  • Se usa el subíndice i para datos transversales: información recopilada en un momento determinado.

  • Se usa el subíndice t para datos de series de tiempo: información reunida a lo largo de un periodo.

Naturaleza y fuentes de datos para el análisis económico

Tipos de datos

• Series de tiempo: conjunto de observaciones sobre los valores de una variable en diferentes momentos, recopilada en intervalos regulares.

  • Ejemplo: PIB.

  • Es estacionaria si su media y su varianza no varían sistemáticamente con el tiempo.

• Series transversales: datos de una o más variables recopilados en el mismo punto del tiempo.

  • Ejemplo: encuestas de opinión Gallup, censos.

  • Cuando hay unidades heterogéneas, debe tomarse en cuenta el efecto de escala.

• Datos combinados: reúnen elementos de series de tiempo y transversales.

  • Ejemplo: IPC entre años son tiempo, pero de varios países son transversales.

• Datos en panel: se estudia a través del tiempo la misma unidad transversal.

  • Ejemplo: varios censos periódicos.

  • Si todos los objetos de estudio tienen el mismo número de "observaciones", es un panel balanceado.

Fuentes de datos

• Internet

  • Pueden ser de naturaleza experimental o no experimental, dependiendo si están sujetos al control del investigador.

Precisión de los datos

1. Errores de medición por aproximaciones.

2. Errores de observación, por acción u omisión.

3. Faltas de respuestas en encuestas, ocasionando un sesgo de selectividad.

4. Los macrodatos muy agregados no muestran sobre las microunidades, como el PIB.

5. Datos de carácter confidencial sólo pueden publicarse de forma agregada.

• El resultado de la investigación será tan bueno como lo sea la calidad de los datos.

Escalas de medición

• Escala de razón: en intervalos constantes, ordenables, el cero es el origen, comparables. (Ej, distancia).

• Escala de intervalo: intervalos iguales y medibles, ordenables, puede asumir valores negativos. (Ej, temperatura).

• Escala ordinal: las categorías se pueden ordenar, pero no medir la distancia entre ellas. (Ej, opciones A, B, y C).

• Escala nominal: no hay orden entre las categorías. (Ej, masculino y femenino).

Resumen

1. La idea fundamental del análisis de regresión es la dependencia estadística de una variable, la dependiente, respecto de otra o más variables, las explicativas.

2. El objetivo de tal análisis es estimar o predecir la media o el valor promedio de la variable dependiente con base en los valores conocidos o fijos de las explicativas.

3. En la práctica, un buen análisis de regresión depende de la disponibilidad de datos apropiados.

   • En este capítulo analizamos la naturaleza, fuentes y limitaciones de los datos disponibles para la investigación, en especial en las ciencias sociales.

4. En toda investigación se debe señalar con claridad las fuentes de los datos para el análisis, sus definiciones, sus métodos de recolección y cualquier laguna u omisión en ellos, así como toda revisión que se les haya aplicado.

   • Tenga en cuenta que los datos macroeconómicos que publica el gobierno con frecuencia son objeto de revisión.

5. Como el lector tal vez no tenga tiempo, energía o recursos para llegar a la fuente original de los datos, tiene el derecho de suponer que el investigador los recopiló de manera apropiada, y que los cálculos y análisis son correctos.