Advanced Algebra 2 Honors Final Review
Chapter 1
%%equation:%% a statement indicating that two quantities are equal
%%the solution set%%: the set of all solutions of an equation
- there can be restrictions on the values of a variable
- ex. x^2+4/x-2. x cannot be 2 because then the denominator would be 0
Types of equations
- identity - every acceptable real number replacement for the variable is a solution
- contradiction - no real number is a solution
- solution set contains some but not all real numbers
%%Linear equations:%% ax+b = 0
%%Rational equations:%% equations that contain rational expressions
%%mathematical modeling:%% the process of finding the equations that describe the words of the problem
Steps:
- Analyze the problem
- Pick a variable to represent the quantity being found
- Find a way to express an amount in two ways
- Form an equation
- Solve
- Answer
- Check
%%complex numbers:%% numbers that are the sum or difference of a real number and an imaginary number
%%imaginary numbers:%% denoted by i
- i = square root of -1
%%complex conjugates%%: complex numbers with different signs
- a+bi and a- bi
The Powers of I:
i = √-1
i^2 = -1
i^3 = -i
i^4 = 1
- the pattern is i, -1, -i, 1
If n is a natural number that has a remainder of r when divided by 4, i^n = i^r
%%quadratic equation%%: an equation that can be written in the form ax^2+bx+c=0 where a, b, and c are real numbers and a doesn’t = 0
%%Zero Factor Theorem:%% If a and b are real numbers and if ab = 0, then a=0 or b=0
%%Square Root Property%%: If x^2 =c, the x=√c 0r x=-√c
Quadratic Formula: x = -b + √b^2-4ac / 2a
%%discriminant:%% the value b^2 -4ac
Polynomial Equation: arrange terms of polynomial in descending order based on the degree and set equal to zero
- a>b if point a lies to the right of point b on a number line
Properties of Inequalities:
- %%The Trichotomy Property:%% for any real numbers a and b, one of the following statements is true: a
- %%The Transitive Property:%% If a, b, and c are real numbers, then: if a<b, then a+c<b+c, a-c<b-c
%%equivalent inequalities%%: inequalities with the same solution set
%%compound inequalities:%% two inequalities put together
- Solve 5<3x-7<=8
Add 7 to all sides
12<3x<=15 divided by 3
4<x<=5 (4,5 ]
%%quadratic inequalities:%% if a doesn’t equal 0, inequalities like ax^2+bx+c
%%rational inequalities%%: inequalities that contain fractions with polynomial numerators and denominators
%%absolute value%%: |x|
|-7| - 7
Chapter 2
%%relation:%% a correspondence between a set of input values and a set of output values
%%domain%%: input values of x
%%range:%% output values of y
%%function:%% any relation that assigns exactly one output value for each input value
- y is dependent and x is independent
- represented through verbal expression, table, ordered pairs, equation, or a graph
function notation: y= f(x)
%%difference quotient:%% f(x+h)-f(x)/ h
%%rectangular coordinate system%%: 2 perpendicular number lines that divide the plane into four quadrants
Linear Equations: Ax+By=C and y = mx+b
- to find y-intercept, replace x with 0.
- horizontal and vertical lines are not functions
%%linear function%%: a function in standard form ax+b=f(x)
Distance Formula
%%d= √(x2-x1)^2 + (y2-y1)^2%%
ex. Find the distance between (-1,-2) and (-7,8)
√(-7--1)^2 + (8--2)^
√-6^2+10^2
√136
= 2√34
Midpoint Formula
%%(x1+x2/2 , y1+y2/2)%%
ex. Find the midpoint of (-7,2) and (1,-4)
(-7+1/2 , 2+-4/2)
(-6/2, -2/2)
(-3,-1)
%%slope%%: the measure of the steepness of a line
- constant rate of change
- change in y over the change in x
- the slope of a horizontal line is 0
- the slope of a vertical line is undefined
slope intercept form: y=mx+b
point slope form: y-y1=m(x-x1)
Parabolas: lowest point is the vertex, symmetric about the y-axis
How to test symmetry:
- to test the x-axis, replace y with -y
- to test the y-axis, replace x with -x
- to test origin, replace y with -y and x with -x
%%circle%%: the set of all points in a plane that are a fixed distance from the center
%%radius:%% fixed distance from the center to a point on a circle
equation of a circle: %%(x-h)^2+(y-k)^2=r^2%%
general equation: ax^2+by^2+cx+dy+e=0
%%ratio:%% the quotient of two numbers
%%proportion:%% an equation indicating that two ratios are equal
- 2/3 = 4/6
- in the proportion a/b = c/d, a and d are the extremes, b and c are the means
- ad=bc
ex. solve the proportion x/5 = 2/x+3
x(x+3) = 2(5)
x^2+3x=10
x^2+3x-10=0
(x+5)(x-2)=0
x=-5,2
hyperbola: the graph of the equation y=k/x
%%direct variation:%% when a variable’s ratio is a constant, y/x=k or y=kx
%%inversely variation:%% when a variable’s product is a constant, xy=k
%%joint variation:%% when y varies jointly with x, y=kwx
Chapter 3
ex. Graph f(x)=-2|x|+3
| x | f(x) |
|---|---|
| 0 | 3 |
| 1 | 1 |
| -1 | 1 |
- graph these points
%%basic functions/parent functions:%% six common functions
- f(x) = x
- f(x) = x^2
- f(x) = x^3
- f(x) = √x
- f(x) = cube root of x
- f(x) = |x|
- the graph of y=f(x)+k is the same as y=f(x), but translated k units up
- the graph of y=f(x)-k is the same as y=f(x), but translated k units down
%%even function:%% symmetric about the y-axis - if f(-x) is f(x)
%%odd function%%: symmetric about the origin
local maximum: y value of a high point
local minima: y value of a low point
- extrema
- local max. occurs where the function changes from increasing to decreasing
- local min. occurs where the function changes from decreasing to increasing
If the ranges of functions f and g are subsets of real #s, then
- (f+g)(x)=f(x)g(x)
- (f*g)(x)=f(x)g(x)
- (f/g)(x)=f(x)g(x)
- (f-g)(x)=f(x)g(x)
composition functions: when one quantity is a function of a second quantity that depends on a third quantity
ex. f(x)=2x+7 g(x)=x^2-1. Find (f*g)(x)
2(x^2-1)+7
2x^2-2+7
2x^2+5
decomposition: reversing the composition process and using a function h
one-to-one functions: functions whose inverses are also functions
ex. Determine if the function is one-to-one: f(x)=x^4+x^2
No, because different numbers can have the same outputs - 2 and -2 have the same output
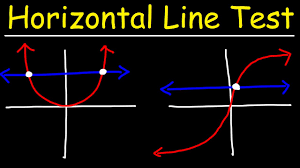
horizontal line test: used to determine if the graph is one-to-one
Properties of One-to-One functions:
- If f is a one-to-one function, there is a one-to-one function f^-1(x) such that
- (f^-1◦f)(x)=x and (f◦f^-1)(x)=x
- The domain of f is the range of f^-1 and the range of f is the domain of f^-1
Finding the Inverse Functions:
- Replace f(x) with y
- Interchange the variables x and y
- Solve the resulting equation for y
- Replace y with f^-1(x)
ex. Find the inverse of f(x)=3/2x+2
2(x)=3/2y+2(2)
2x=3y+4
2x-4=3y
y=2x-4/3
f^-1(x)=2x-4/3
- the graph of a function and its inverse are reflections of each other about the line y=x
Chapter 4
quadratic function: second-degree polynomial function
- f(x)=ax^2+bx+c
To graph a quadratic function:
- Determine if the parabola opens up or down
- Find the vertex
- Find the x-intercepts
- Find the y-intercepts
- Identify one additional point
- Draw a curved line through these points
Polynomial Functions:
- cannot have a fraction, radical, negative exponent, or an absolute value
- the graph is a smooth continuous curve
zero: a value of x for which f(x)=0
power function: polynomial function in the form f(x)=a^n
- end behavior is the same as the graph of its term with the highest degree
To graph of polynomial functions:
- Find x and y intercepts
- Determine end behavior
- Make a sign chart and determine where the graph is above and below x-axis
- Find symmetries
- Plot points and draw graph as a smooth continuous curve
- \