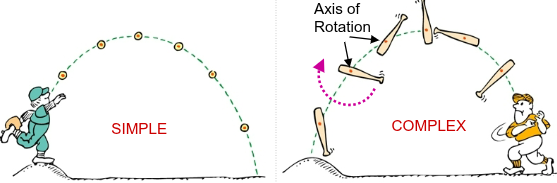
Chapter 11 - Rotational Motion

• In physics we distinguish two types of motion for objects:

  • Translational (Linear) Motion - change of motion

  • Rotational Motion - change of orientation

  

  • In linear kinematics, we had measurements and variables which we used to describe the motion of an object

  • We need to ‘redefine’ and ‘rename’ these since now they will be for rotational kinematics

• Variables for Linear Kinematics:

  Measurement Variable Unit

  Time t s

  Displacement Δx, Δy m

  Velocity v_i, v_f m/s

  Acceleration a m/s²

• Variables for Rotational Kinematics:

  Measurement Variable Unit

  Time t s

  Displacement θ rad (radians)

  Velocity ω rad/s

  Acceleration α rad/s²

• Everything in rotational kinematics we have already done in linear kinematics, so all of the concepts stay the same

• There are 2 types of pure unmixed motion:

  • Translational - linear motion

  • Rotational - motion involving a rotation or revolution around a fixed chosen axis (aka an axis that doesn’t move)

• We need a system that defines BOTH types of motion working together on a system

  • Rotational quantities are usually defined with units involving a radian measure

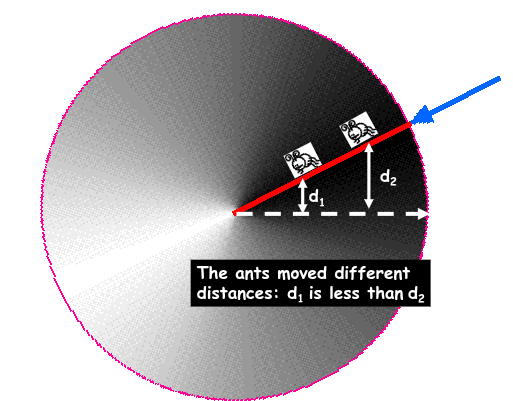
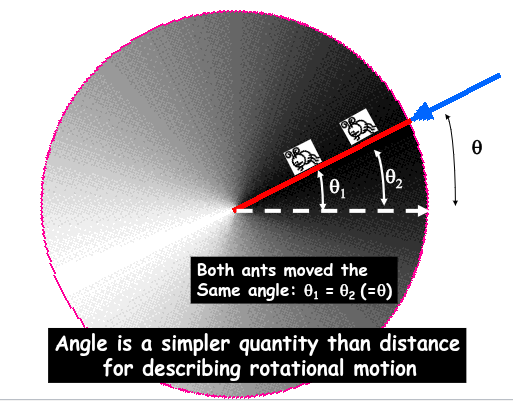
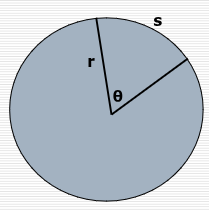
    • If we take the radius of a circle and LAY IT DOWN on the circumference, it will create an angle whose arc length is equal to R

    • In other words, one radian angle subtends an arc length s equal to the radius of the circle (R)

      

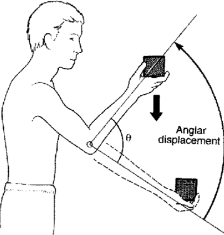
  • Displacement, measured in θ, is measured in radians

  • Just like linear, we have to include the direction

    • Counterclockwise is positive

    • Clockwise is negative

      

  • One revolution is 2π radians (aka 360°)

    • 1 rev = 360° = 2π

  • θ (in radians) = Arc length / Radius

  • θ = s / r

    

  • Velocity is measured in rad/s,

  • ω = θ / r

  • Acceleration is measured in rad/s²

  • α = Δω / t

  v_f = v_i + at ———> ω_f = ω_i + αt

  Δx = v_it +½ at² —> θ = ω_it + ½ αt²

  v_f² = v_i² + 2aΔx —> ω_f² = ω_i² + 2αθ

  Δx = ½ (v_i + v_f)t -> θ = ½ (ω_f + ω_i)t

  • We can now do kinetic problems like we used to, except for the variable change

  • To succeed here, remember our new variables and terms

• There is a way to link rotational and linear kinematics

  v_tan = rω

• This equation uses the angular velocity and ‘converts’ it to linear, or translational velocity

Torque

• Torque is the ‘rotational equivalent’ of force

• Torques make objects change their rotational velocity (ω)

• Torque is defined as:

  τ = F_⊥ℓ

• Torque is considered:

  • positive when the force tends to produce a counterclockwise rotation about the axis

  • negative when the force tends to produce a clockwise rotation

• The last equation is known as

  τ = Iα

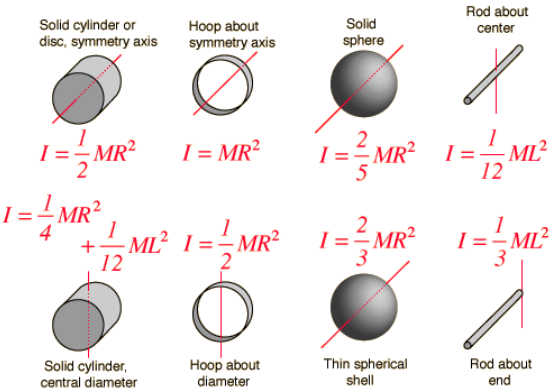
  • The moment of inertia is kind of like ‘mass’ but different objects rotate differently, so depending on the object and the distribution of the mass, there are different moments of inertia

    

Rotational Kinetic Energy

• Kinetic energy is the energy of motion

• When you ‘spin’ or ‘rotate’, you are in motion

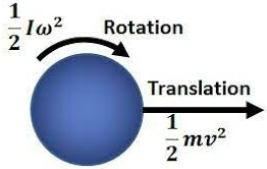
• We will call our linear/translational motion kinetic energy is KE_trans

  KE = ½mv² —> K=1/2Iω²

  

Rotation, Angular Motion & Angular Momentum