Internal Energy

• The atoms/molecules which make up a real object can have energy even though the object itself does not appear to have any.

  • The atoms/molecules can move around and collide with each other which implies they have kinetic and potential energy.

  • The atoms in a molecule are held together by forces which also implies potential energy.

  • Atoms in a molecule can vibrate and rotate both of which are forms of kinetic energy.

• The sum of the energy of all the atoms/molecules in an object is called the object’s internal energy.

  • Internal energy does not include the kinetic and potential energy of the object as a whole.

• There are two factors that affect internal energy:

  • How many atoms/molecules there are,

  • The average internal energy per atom/molecule.

Temperature

• The temperature of a body is a measure of the average kinetic energy of the atoms/molecules within it.

• Many properties of objects change as the temperature changes.

  • volume, pressure, electrical resistance

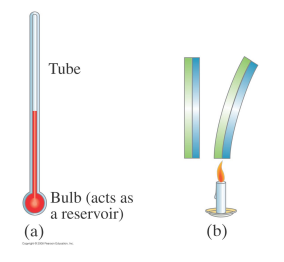
• Thermometers are devices to measure temperature.

• They all use a temperature-dependent property of the device material (such as its volume) to determine the temperature.

  • liquid-in-glass thermometers use the volume of a liquid (mercury)

  • a bimetallic strip uses the expansion of two different metals

    

Temperature Scales

• In order to measure a temperature, a thermometer needs a scale.

• Temperature scales assign numerical values for the temperature of one or more substances under given conditions.

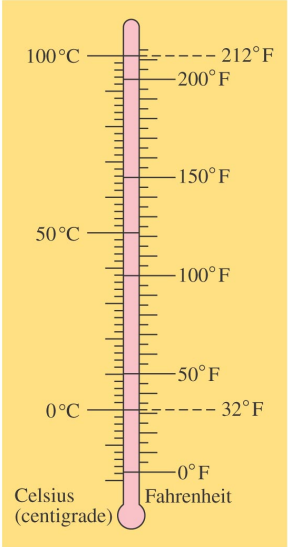
  • The Celsius or Centigrade scale assigns 0°C to the freezing point of water under atmospheric pressure and 100°C to its boiling point.

  • The Fahrenheit scale assigns 32°F to the freezing point of water under atmospheric pressure and 212°F to its boiling point.

• To convert:

  • T (˚ F)=9/5T (˚C)+32

  • 0 °C = 32 °F

    

EXAMPLE 1

Normal body temperature is 98.6°F. What is this on the Celsius scale?

• T (˚ F)=9/5T (˚ C)+32 T (˚ C)=5/9 [ T(˚ F)−32] T (˚ C)=37 ˚ C

EXAMPLE 2

When you say that body A has a higher temperature than body B, you are comparing the:

• A. internal energy.

• B. mass.

• C. kinetic energy per particle.

• D. potential energy.

The Gas Laws

• For a fixed amount of a dilute gas well above the liquefaction (boiling) point, it was found experimentally that at fixed temperature

  • P∝ 1 / V

  • PV=constant

• This is known as Boyle's Law.

Charles' Law

• After Boyle, it was found by Charles that the volume of a fixed amount of a dilute gas at fixed pressure was proportional to its temperature.

Absolute Zero

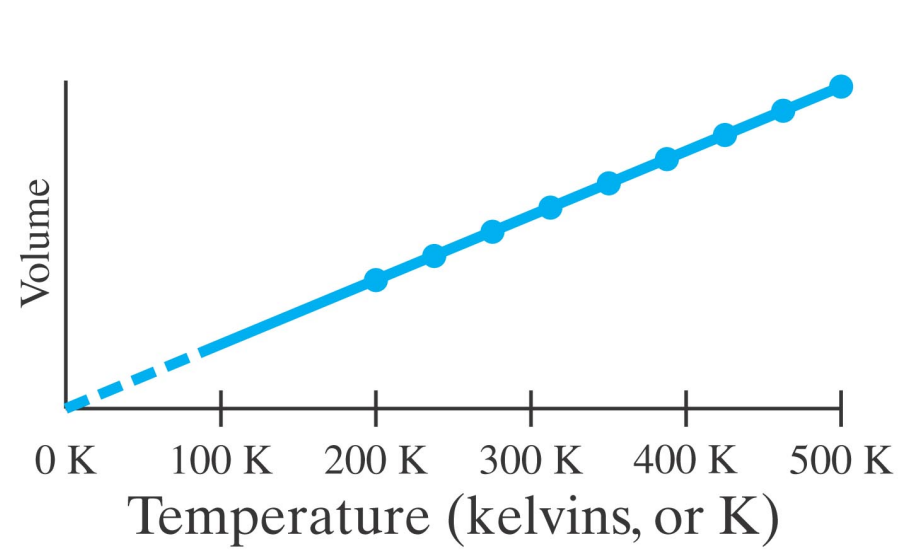
• Charles found the same amount of all dilute (ideal) gases follow the same line.

• At a temperature of -273.15°C the volume of any dilute gas would be zero.

• This temperature is called absolute zero - it is the coldest possible (real) temperature any object can have.

• The discovery of absolute zero led to a new temperature scale called the absolute or Kelvin scale – units are kelvins K.

  • one of the fixed points of the scale is absolute zero and is given the temperature of 0 K, the other is the triple point of water T = 273.16 K.

  • a change of temperature of one kelvin is the same as one Celsius.

    • T (K)=T (˚C)+ 273.15

• The Rankine temperature scale, °R, is similar to the Kelvin scale but a change of 1 K is equivalent to 1.8 °R.

• Using the Kelvin scale the line in the V versus T figure for Charles' law passes through the origin.

  • On the Kelvin scale, there are no (real) negative temperatures.

Gay-Lussac's Law

• It was found by Gay-Lussac that, at a fixed volume, the pressure of a fixed amount of a dilute gas was proportional to the absolute temperature.

  • P∝T

• As with Boyle's Law, the pressure is the absolute pressure, not the gauge pressure.

• All three gas laws can be combined into the Ideal Gas Law.

  • PV ∝T

Heat

• The internal energy of a body can be changed in three ways:

  • we can add or subtract matter,

  • we can do work upon the body or it can do work on something,

  • we can add or extract heat.

• In order to add heat to, or subtract heat from, a body we put it in thermal contact with another body at a different temperature.

  • A thermal contact does not allow any exchange of matter or allow the second body to do work on the first.

• Heat is the energy transferred from one body to another due to temperature differences.

• Heat is transferred by conduction, convection or radiation.

• Heat is not the same as internal energy, it is the energy transfer that is not via work or by changing the amount of an object.

• Heat is measured in joules.

• Other common units are the calorie, kilocalorie (Calorie), Btu, ...

  • One calorie (cal) = 4.186 J, is the energy needed raise the temperature of 1 g of water from 14.5°C to 15.5°C.

  • A kilocalorie (kcal) is 1000 calories. (Sometimes, especially on food packaging, a kcal is called a Calorie)

  • One British thermal unit (Btu) = 1056 J, is the energy needed raise the temperature 1 lb of water by 1°F.

Specific Heat (Liquids and Solids)

• If an amount of heat Q flows into an object then its temperature rises, there is a change in temperature ΔT.

• The change in temperature depends upon the mass of the object and what the object is made from.

• The relationship between Q and ΔT is written as

  • Q=m c Δ T

• The 'constant' c is called the specific heat capacity.

• Its units are J /kg /K or J /kg /°C.

• The product C = m c is often called the heat capacity.

• The molar heat capacity, confusingly also often denoted by C, is the amount of heat required to raise one mole of a substance by 1°C.

• The specific heat is different for each chemical substance and phase.

• The specific heat for solids and liquids does not change much with temperature and pressure.

  • If the temperature change is small the specific heat is constant.

• Liquids tend to have higher specific heat than solids.

• According to theory, black holes have negative heat capacity!

EXAMPLE 1

The same quantity of heat is added to different amounts of water in two equal-size containers. Which gets the hottest?

• The container with less water will get hotter since there is less water to absorb the heat energy.

EXAMPLE 2

You heat a half-cup of tea and its temperature rises by 4°C. How much will the temperature rise if you add the same amount of heat to a full cup of tea?

• Assuming the same type of tea and same initial temperature, the temperature rise will be the same for both half-cup and full cup. Therefore, adding the same amount of heat to a full cup of tea will also result in a temperature rise of 4°C.

EXAMPLE 3

Two equal-mass liquids, initially at the same temperature, are heated for the same time over the same stove. You measure the temperatures and find that one liquid has a higher temperature than the other. Which liquid has a higher specific heat?

• The liquid with the higher specific heat would have a lower final temperature. This is because a substance with a higher specific heat requires more heat energy to raise its temperature compared to a substance with a lower specific heat. So, if two equal-mass liquids are heated for the same time with the same amount of heat, the one with the higher specific heat will experience a smaller temperature increase than the one with the lower specific heat.

EXAMPLE 4

Two objects are made of the same material but have different masses and initial temperatures. If the objects are brought into thermal contact, which one will have the greater temperature change?

• The object with the smaller mass will have the greater temperature change. This is because the amount of heat required to raise the temperature of an object depends on its mass, with more heat required for larger masses. Therefore, when two objects with different masses and initial temperatures are brought into thermal contact, heat will flow from the warmer object to the cooler one until they reach thermal equilibrium, with the final temperature being somewhere in between the initial temperatures. The smaller object will heat up more quickly, because it requires less heat to raise its temperature, while the larger object will heat up more slowly.

EXAMPLE 5

You heat 100 g or iron nails to 100 °C. You then dump the hot nails in 100 g of well-insulated water which has a temperature of 20 °C. Estimate the final temperature of the water.

• Around 30 °C

• The heat lost by the nails as they cool is the heat gained by the water. Because the heat capacity of water is much larger than iron, the heat added to the water causes a smaller change in the temperature of the water. The heat removed from the nails causes a big change in the temperature of the nails.

Thermal Expansion

• Most substances expand in volume when heated and contract when cooled (water between 0°C - 4°C is an exception).

• The amount of expansion depends upon the material.

• The expansion is in all three dimensions but can be divided into linear expansion and volume expansion.

  • The linear expansion measures the change in one dimension – the length– of an object made of a particular material,

  • The volume expansion measures the change in volume.

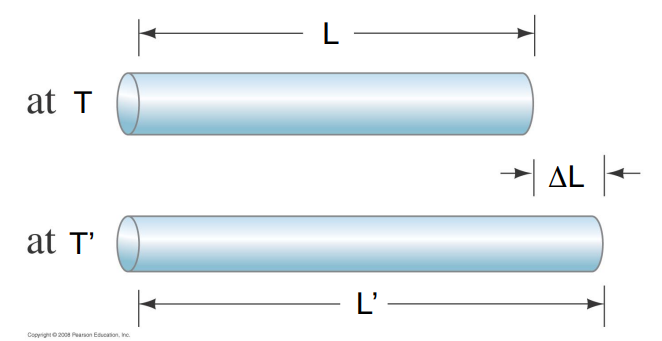
• The increase in length of an object, ΔL, for a given temperature increase, ΔT, is proportional to the length L of the object at the initial temperature.

• For small temperature changes it is found that the change in length is proportional to the increase in temperature.

  • Δ L=α LΔT

• The quantity α is called the coefficient of linear expansion.

• For liquids and gases (at fixed pressure) linear expansion doesn't make much sense because fluids have no fixed shape.

• Instead, we can measure the increase in volume.

• It is found the increase in the volume of a fluid, ΔV, for a given temperature increase, ΔT, is proportional to the volume V of the fluid at the initial temperature.

• For small temperature changes it is found that the change in volume is proportional to the increase in temperature.

  • ΔV =βV ΔT

• If a solid increases by the same fraction in all 3 dimensions then we expect

  • β≈3 α

• Liquids typically expand more than solids.

• Over wide temperature changes it is found α and β do depend upon the temperature T.

• Although the coefficients of linear expansion are usually small, the change can be noticeable/important.

• For example, consider the steel bed of a suspension bridge which is 200 m long at 20°C. If the extremes of temperature to which it might be exposed are -30°C to +40°C, the bridge length will change by 16 cm.

• If one part of a glass is heated, the expansion can generate forces that can cause the glass to break.

• If you fill a container to the brim with a liquid early in the morning, later in the afternoon you will find the liquid has overflowed (assuming it hasn’t evaporated).

Water

• Water is a very peculiar substance: below 4°C water will expand as it cools.

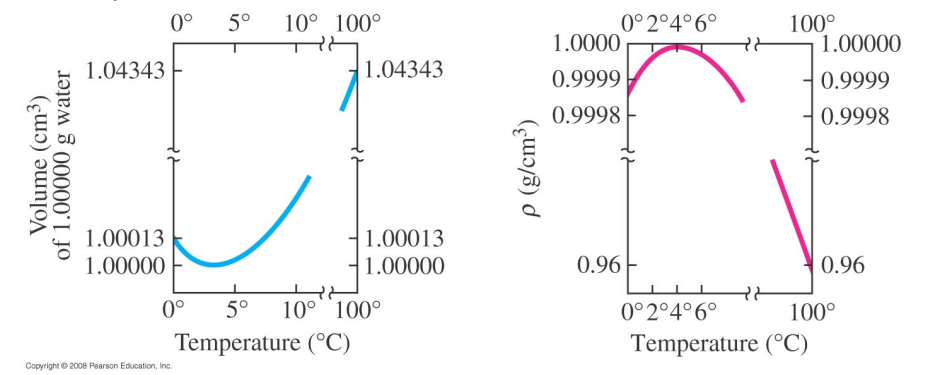
• Water at 0°C will float on top of water at 4°C therefore ice will form at the surface first.

• Furthermore, when water freezes it expands even further.

• Unlike most substances, water freezes from the top down.