Ratios

• Ratios show the relationship between two (or more) numbers. They can be written as or (Ex. 2 eggs per every cup of flour in a recipe can be written as 2:1 or )

Simplifying Ratios

• Ratios can be simplified just like fractions because they can be written as fractions (Ex. because both 6 and 12 are divisible by 6)

Simplifying Ratios with Decimals/Fractions

• First, multiply the entire ratio by a number to get the ratio in all whole numbers. Then, further, simplify as normal if possible.

  • For fractions, you would need to multiply by the common denominator to get the ratio in all whole numbers

Simplifying Ratios in Different Units

• Convert one of the units to the other (usually the larger unit to the smaller one) and then simplify (Ex. 25 mm:5 cm = 25 mm: 50 mm = 1:2)

Writing Ratios as Fractions of a Whole

• When the ratio expresses a relationship between two parts of a whole, you can add the ratio values to find the total amount. Then you use the ratio values as numerators for different fractions with the same total amount as your denominator. Then you can express parts of a whole (Ex. 2 purple squares: 3 blue squares -> 5 squares in total. squares are purple and squares are blue)

  • Useful for questions that ask how much of something each person gets based on a ratio (Ex. There are 25 squares available. How many squares are purple and blue based on the ratio of 2 purple squares: 3 blue squares? You would solve this by multiplying the and fractions by 25 to find the number of each)

Scale Factors

• Scale factors are numbers which scale or multiplies a quantity. They are usually used for maps and scaled diagrams like floor plans.

• To convert from a scale drawing to real life size, measure a line in the drawing and multiply by the scale factor, which would be given.

• To convert from real life size to a scale drawing, divide the real life measurement by the scale factor.

Percentages

• A percentage is a proportion that shows a number as parts per hundred (Ex. )

  • They can be written as fractions or decimals too (Ex. )

Calculating Percentages of Amounts

• To calculate the percent of an amount, convert the percent into a decimal or fraction and then multiply it by the amount (Tip!: Usually convert the percentage into a fraction when solving without a calculator because it’ll be easier to solve)

  • Ex. of 50 = = 10

Increasing/Decreasing an Amount by Percentages

• To increase an amount by a percentage, calculate the percentage of the amount and add that value to the amount.

• To decrease an amount by a percentage, calculate the percentage of the amount and subtract that value from the amount.

• Another way is that you can find the percentage of the amount that would result after adding or subtracting the percent from 100%. Then you would multiply that new percentage by the amount given

  • Ex. Increase 50 by 8% = 100%+8% is 108% = 1.0850 = 54

  • Ex. Decrease 72 kg by 40% = 100%-40% is 60% = 0.672= 43.2

• To find the multiplier for a certain percent increase or decrease, you just increase or decrease that percent from 100% and convert that value into a decimal

To Find the Percentage

• Divide the part value by the total value to find the decimal, then multiply that result by 100% (Ex. 18 points out of 20 total = = 0.9100% = 90%)

• Also can write the part value over total value as a fraction, and then find an equivalent fraction with the denominator out of 100 (Ex. 18 points out of 20 total = = = 90%)

To Find Percent Change

• Percent Change=

• You determine it is a percent gain if the value increases from the original to current value and it’s a percent loss if the value decreases from original to current value

Reverse Percentages

• Reverse percentages are used to find the original price or value of an item after it has increased or decreased in value. The original value is always represented by 100%

• When the value after an increase or decrease is given, first find out how much percent of the original the value represents (the percent could be above or below 100%). Then, convert that percentage to a fraction and set it equal to the value after the increase or decrease. Multiply both sides by the reciprocal of the fraction to find the original value.

  • Ex. 20% off a shirt is $24. So 100%-20%=80%, which is the percent of the original that $24 represents. 80% as a fraction is , which is set equal to 24 as . Then, . When simplified you get 1=30. The original value of the shirt was $30.

Interest Rates

• Interest is money that is paid back regularly to a bank or person at a particular percentage when you loan or borrow money

Simple Interest

• Simple Interest is a quick way of calculating interest where you find the percentage amount of interest for one period (year, month, etc.) and then you multiply that amount by the number of periods that money will be spent for. Then you add that value to the amount borrowed.

  • Ex. Borrowing $40 for 3 years when the simple interest rate is 5% per year. 5% of 40 is $2. $23=$6. $40+$6=$46 owed.

Compound Interest

• Compound interest is a type of interest where each time interest is paid onto an amount, the added interest plus the previously accumulated amount also receives interest from then on.

• Multiplier Method= Use the percentage and turn it into a multiplier (100%+5%= 105%= 1.05). Then, for every calculation you can multiply by the multiplier (Using powers to make it even faster when time periods are large)

  • Ex. Borrowing $40 for 3 years when the compund interest rate is 5% per year.

$401.05= $42

$421.05= $44.10

$44.101.05= $46.31

OR

$40= $46.31

Proportions

• Proportions are two ratios (usually written as fractions) set equal to each other and used to calculate missing values when one ratio is known.

• When given a ratio and one value of the other ratio, you can set up a proportion with the ratios (making sure the units of the numerators and denominators match each other). Then you can multiply by the reciprocal of the known ratio to find the missing value.

  • Ex. 8 pens cost $2.16. Calculate how much 7 pens cost.

Scale Factors

• You can also use proportions to find out how much bigger one shape is compared to a smaller one, which is called a scale factor

• To find a length scale factor, divide the bigger length by the corresponding smaller length.

  • Note!: To calculate the area scale factor (area and surface area), square the length scale factor. To calculate the volume scale factor, cube the length scale factor.

Proportionality

• To write equations with proportions:

1. Write the proportional relationship

2. Convert to an equation using a constant of proportionality (

3. Use given information to find the constant of proportionality

4. Substitute the found constant of proportionality into the equation

Direct Proportions

• A direct proportion is a relationship between two values where the multiplier is always the same (they are multiples of each other). The symbol for direct proportions is ∝. The graph for direction proportions is linear.

  • Ex.

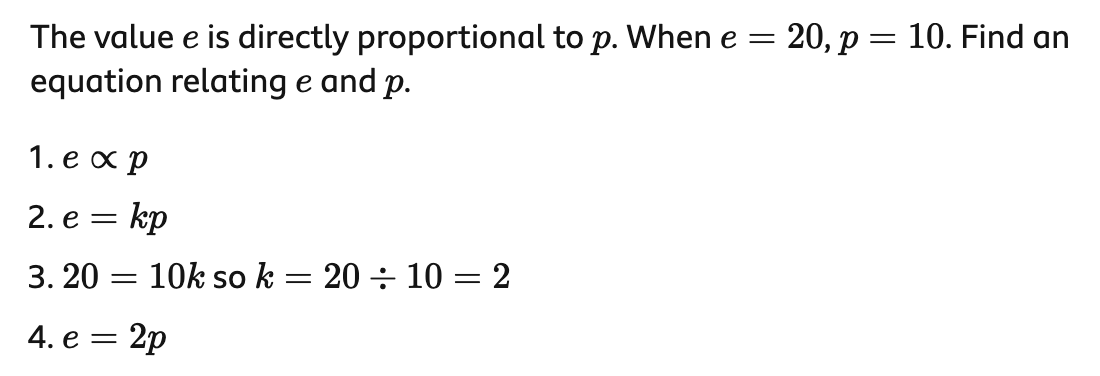
Indirect Proportions

• An indirect proportion is a relationship between two values where when one value increases, the other decreases. The symbol for indirect proportions is ∝. The graph for indirect proportions is exponential decay.

  • Ex.

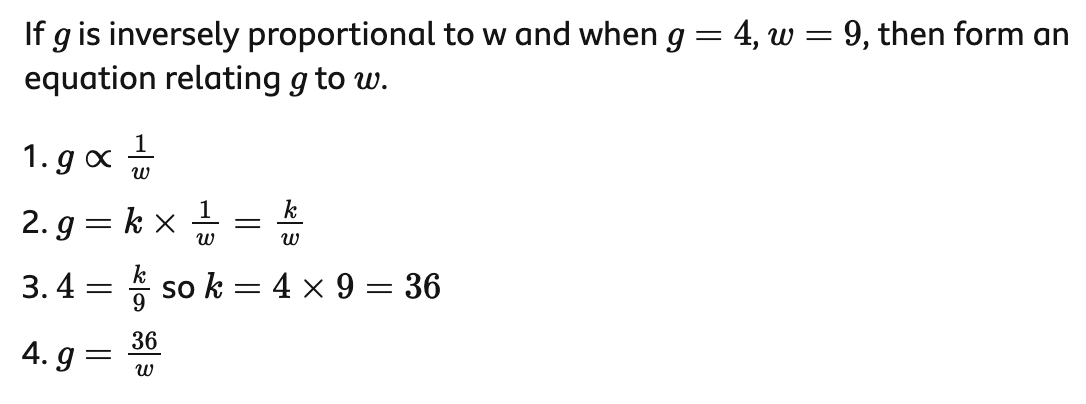
Exponential Growth and Decay

• Exponential graphs have the formula

  • When is greater than 1 (, then it’s exponential growth

  • When is less than 1 and greater than 0 , then it’s exponential decay