INTRODUCTION TO PHYSICS (4)

• The study of motion is an integral part of physics. The motion, however, can be in more than one dimension.

• Motion in three dimensions can be compared to motion in one direction in a similar way that driving in a car (one dimension) can be compared to landing an airplane (three dimensions.)

POSITION AND DISPLACEMENT

• A general way to look at a particle/particle-like object is by its vector with reference to origin (or another reference point). This unit vector can be written as:

  

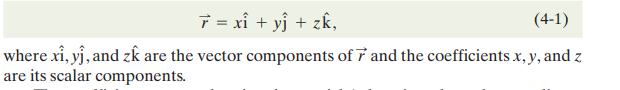
• When the position vector of a particle changes, its displacement is said to change.

• The change in displacement can be determined by subtracting the original displacement from the new displacement.

AVERAGE AND INSTANTANEOUS VELOCITY

• We already know that the terms average and instantaneous velocity define ‘how fast’ an object moves. However, now we will be seeing these quantities in vector notation.

• When we speak of the velocity of a particle, we usually mean the particle’s instantaneous velocity at some instant. This value approaches in the limit as we shrink the time interval t to 0 at that instant.

• The direction of the instantaneous velocity of a particle is always tangent to the particle’s path at the particle’s position.

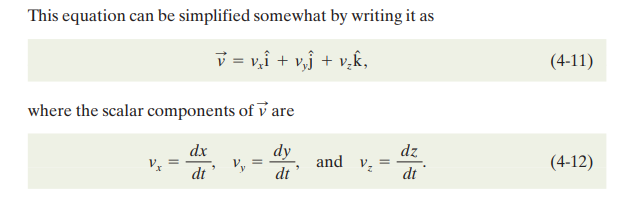AVERAGE AND INSTANTANEOUS ACCELERATION

• As the velocity of an object changes per unit time, it is said to accelerate.

• As we shrink time to zero about some instant, then the limit approaches the instantaneous acceleration (or acceleration) at that instant.

• If even one magnitude or direction of the velocity changes, the object accelerates.

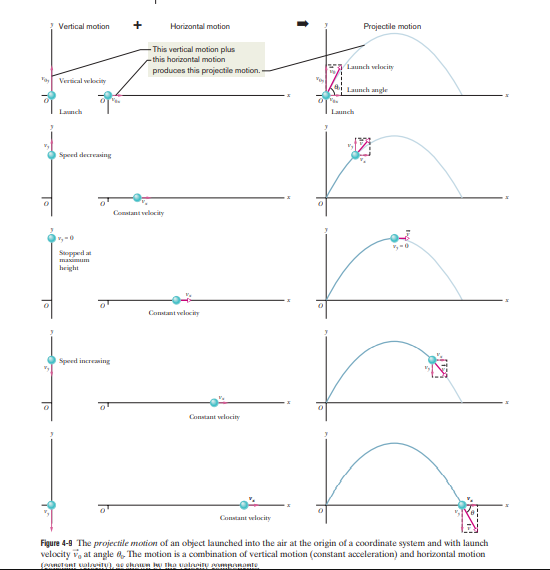
PROJECTILE MOTION

• Projectile motion is a special case of two-dimensional motion.

• This is when a particle moves in a vertical plane with some initial velocity but its acceleration is always the free-fall acceleration, which is downward.

• The position vector and velocity vector are both continuously changing but there is no horizontal acceleration because its acceleration vector is always constant and downward. This can be simply written as:

• In projectile motion, the vertical and horizontal motion are independent of each other; that is, neither motion affects the other.

• To make this two-dimensional projectile motion easier, we divide it into two parts of one dimensional motion: one for the horizontal motion (with zero acceleration) and one for the vertical motion (with constant downward acceleration).

• The following diagram explains this properly:

HORIZONTAL MOTION IN PROJECTILE MOTION

• The velocity in the horizontal motion remains constant because there is no acceleration in the horizontal direction.

• At any time t, the projectile’s horizontal displacement x 1 x0 from an initial position x0 is given by (when a=0):

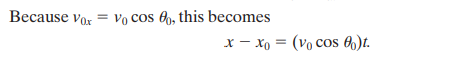
VERTICAL MOTION IN PROJECTILE MOTION

• Most important is that the acceleration is constant. Thus, the equation applies, provided we substitute g for a and switch to y notation. Then:

• 

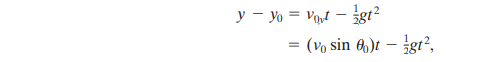
• It is directed upward initially, and its magnitude steadily decreases to zero, which marks the maximum height of the path.

• The vertical velocity component then reverses direction, and its magnitude becomes larger with time.

EQUATION OF THE PATH

• The equation of the trajectory, i.e. the projectile’s path, is determined by eliminating t.

• 

• All these calculations have been taken by assuming that the air has no effect.

• In reality, sometimes the calculations and actual motion vary largely due to the air’s effect, particularly the air resistance which opposes motion.

UNIFORM CIRCULAR MOTION

• If a particle travels around a circle or around a circular arc at a constant/uniform speed, it is said to be in a circular motion.

• While the speed is constant, the velocity is changing due to the continuous change in direction. Therefore, the particle is continuously accelerating.

• In circular motion, the direction of velocity is always tangent to the circle.

• The direction of acceleration is radially inward. Therefore, the acceleration of circular motion is called centripetal acceleration.

• The magnitude of this acceleration is given by dividing the square of speed of the particle, v^2, by the radius of the circle, r.

• The time period for the particle to go around the circumference exactly once is given by dividing the distance of the circumference of the circle by the speed. The circumference is given by 2*pi*r where r is the radius.

• 

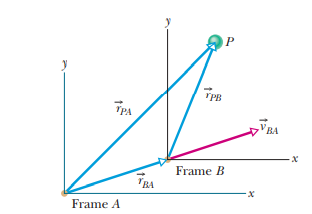
RELATIVE MOTION IN ONE DIMENSION

• The velocity of a particle depends on the reference frame of whoever is observing or measuring the velocity.

• For our purposes, a reference frame is a physical object to which we attach our coordinate system, which is usually the ground.

• Observers on different frames of reference that move at constant velocity relative to each other will measure the same acceleration for a moving particle.

RELATIVE MOTION IS TWO DIMENSIONS