Quantum mechanical model of atoms 

Wave properties of electrons

Schrödinger used wave function to describe amplitude of electron wave as a function of position and time. ==He pictured the electron as a continuous charged cloud of finite size carrying a charge density that is proportional to square of wave function at any point.== Equation showed stationary waves of electrons can form around the nucleus of an atom, and the corresponding energies and energy differences were in good agreement with the experimental values.

Electron wave existence was hypothesized by De-broglie first.

\

Atomic orbitals

==A function describing shape and regions in space of electrons.==

More electrons means more orbitals needed.

The numerals (1 in 1s) are principal quantum numbers they represent energy levels and distance from nucleus of the electron.

The letters (s in 1s) designate the shape of the orbital.

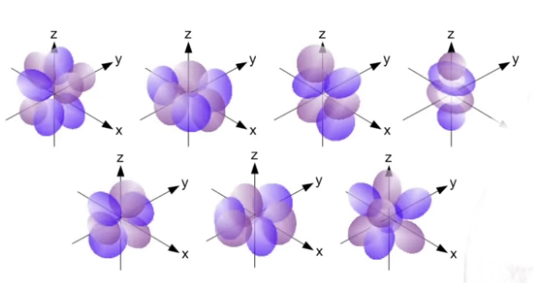
Types

• s orbital: it is spherical and symmetrical around the nucleus. Holds only 2 electrons.

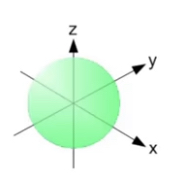
• p orbital: it has a dumbbell shape and holds 6 electrons. They can be arranged at right angles to each other along x, y and z axis.

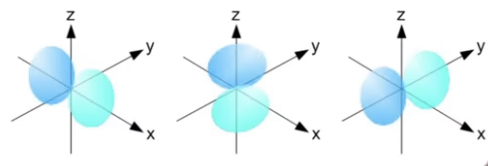
• d and f orbital: d holds 10 electrons and f holds 14. Their shapes are more complex.

Molecular Orbitals(MO)

Formed from pairs of atomic orbitals.

- For sigma bonds we have a bonding molecular orbital or an anti-bonding molecular orbital, when the s orbitals get hybridised they overlap and have no node between them it is bonding molecular orbital. Electrons go to the anti bonding MO when they get excited

- For pi bonds it refers to the second bond in electron bonding. Non-hybridised p orbitals form a plane through the electron but when they get excited they jump to the pi* MO which has a node separating the bonding.

In many molecules some AOs are not involved in bonding.

<<Recommendation: Leah4sci’s video on Molecular orbital theory.<<

\

Quantum numbers

They define values of quantities.

1. Principal(n) - defines energy of electron, e.

The higher n (1,2,3) the farther away from the nucleus. En = E1/n2

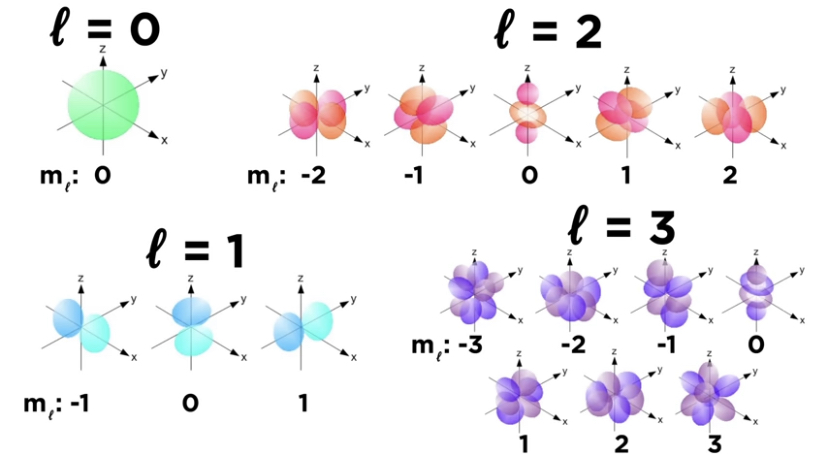
2. Orbital(l) - defines magnitude of angular momentum for orbital and shape. Between 0,1,2, n-1. when l=0 it is s orbital, l=1 is p orbital, etc.

3. Magnetic(ml) - defines angular momentum direction. Tells how many types of an orbital is present, ranges from -l … l ;-2,-1,0,1,2.

   

4. Spin(ms) - defines magnitude of spin. Either +1/2 or -1/2.

   \

==Pauli exclusion principle states that no two electrons can have exactly same four quantum numbers because orbitals hold 2 electrons but will always have opposite spin values.==

Hunds rule states that orbitals in a subshell are occupied singly before they are doubly occupied.

\

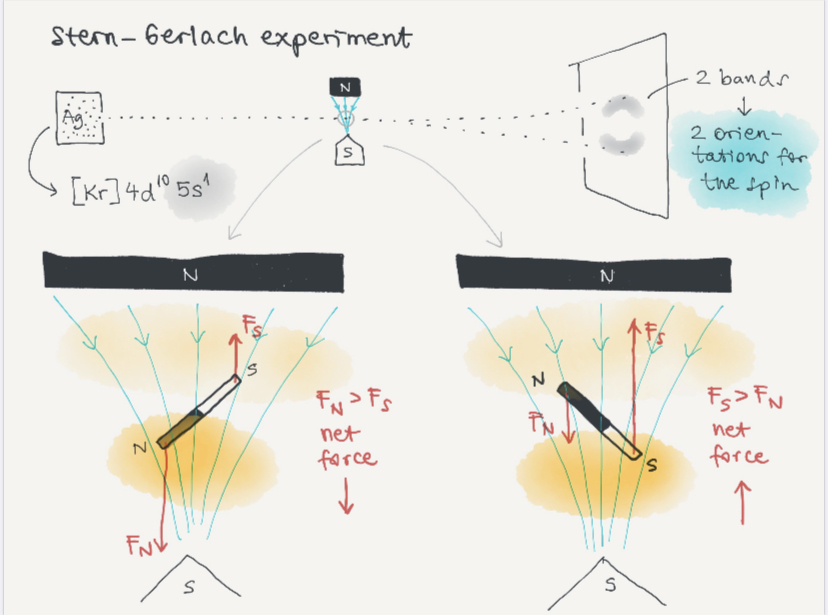
Stern Gerlach experiment

==If a beam is passed through a homogeneous field the forces exerted on the opposite side of the pole cancel each other so only torque is observed. Whereas in an inhomogeneous field the force on one side of the pole will be slightly greater than the other.==

==Atoms that pass through inhomogeneous magnetic field will be deflected, depending on their magnetic momentum. The silver beam used in the experiment was split into two parts and beams of other materials also left discrete traces proving the quantized nature of angular momentum==.

Einstein-de Haas experiment

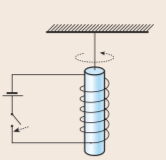
==A tiny iron bar is fixed on a narrow torsion string inside a solenoid. After switching on the current the iron bar is magnetized(magnetic moments are in the same direction) making the bar turn. This is because when magnetized, their angular momentum are also in same direction.== The experiment proves that the effect is caused by the spin momentum.

\
Energy states of molecules

The lowest energy level of a molecule is called the ground state and if it is at higher energy level it is said to be at excited state.

\
\
Disclaimer:

I do not own rights to any of these images.

\