Multivariable Calculus Unit 2 (not broken flashcards)

13.1 Vector Value Functions

Trigonometric Parametrizations to Know

1. Circle:

   • Standard equation: x^2 + y^2 = r^2

   • Parametrization:

     • x(t) = r cos(t)

     • y(t) = r sin(t)

     • where t ∈ [0, 2π]

2. Ellipse:

   • Standard equation: (x^2/a^2) + (y^2/b^2) = 1

   • Parametrization:

     • x(t) = a cos(t)

     • y(t) = b sin(t)

     • where t ∈ [0, 2π]

3. Helix:

   • Standard parametrization:

     • r(t) = <a cos(t), a sin(t), bt>

     • where a is the radius and b is the vertical spacing per unit rotation

     • t ∈ [0, 2πn] for n full turns

4. Spiral:

   • Standard polar equation: r = a + bθ

   • Parametrization:

     • x(t) = (a + bt) cos(t)

     • y(t) = (a + bt) sin(t)

     • where t is the parameter (often taken to be θ, the angle)

5. Sine Wave:

   • Standard form: y = A sin(kx)

   • Parametrization:

     • x(t) = t

     • y(t) = A sin(k * t)

     • where t is a variable, and A and k are constants.

13.2 Calculus of VVFs

• Product Rule

• Chain Rule

  • d/dt (r(g(t)) = r’(g(t)) * g’(t)

• Dot Product

  • both vectors must be differentiable

    

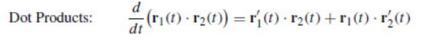
• Cross Product

  • ORDER MATTERS

• Tangent line at r(t₀)

  • L(t) = r(t) + t(r’(t))

• The tangent vector in a vector parametrization is r’(t₀) is horizontal and nonzero if y’(t₀)= 0 but x’(t₀) is not

• General Antiderivative for r(t)

• Fundamental Theorem of Calculus for Vector-Valued Functions

13.3 Arc Length and Speed

• Length of a Path Formula

• Speed at Time t Formula

  • ds/dt = ||r’(t)||

• Arc Length Parametrization

  1. Start with parametrization r(t) such that r’(t) is not equal to 0 for all t

  2. Use the arc length integral

     1. As long as ||r’(t)|| is not equal to 0, s = g(t) is an increasing function and has an inverse t = g^-1(s)

  3. After solving for t in terms of s → r₁(s) = r(g^-1(s))

  • Notes about Arc Length Parametrization

    • ||r’(s)|| = 1 (check to prove that it’s an arc length parametrization)

• Parametrizing a Circle (REVIEW)

• EQUATION OF A HELIX

  • r(t) = <a cos(t), a sin(t), bt>

    • a is radius of helix

    • b is vertical spacing between turns of the helix

    • in the xy-plane and linear motion along x-axis

    • for the angular parameter, divide total height ascended by number of revolutions and divide by 2pi

Integration Review:

• Trig Sub

• Integration Formulas