What is Chemistry?

• study of matter

• the study of the interactions of matter

• study of valence electrons - since they are more unstable than innermost electrons

• conservation laws

  • mass

  • energy

  • electrons

  • charges

Quantum Mechanical Model of the Atom

Schrodinger’s Cat

• electrons can behave like waves and particles

Beginnings of Quantum Mechanics

• until the 20th century, it was believed that all physical phenomena were deterministic

• work done at the time by famous physicists discovered that for sub-atomic particle, the presnet condition does not determine the future condition

• quantum mechanics forms the foundation of chemistry—periodic table, behavior of the elements in chemical bonding

Behavior of Electrons

• electrons are incredible small

• electron behavior determines the behavior od atoms

• directly observing electrons in the atom is impossible bc observing it can change its behavior

• observe electrons like particles, it will behave like one (same for waves)

A Theory that Explains Electron Behavior

• quantum mechanical model explains the manner in with electrons exist and behave in atoms

• helps us understand and predict the properties of atoms

Light in its Wave Nature

• light is a form of electromagnetic radiation

  • composed of perpendicular oscillating waves, one for electric field and one for magnetic field

• All electromagnetic waves move through space at the same, constant speed

  • 3.00 × 10 to the 8th m/s

Characterizing Waves

• amplitude is the height of the wave

  • distance from the mode to the crest

  • measure of how intense the light is

• wavelength is a measure of the distance covered by the wave

  • from one crest to the other

• frequency is the amount of waves that pass through a point in the given time

  • # of waves = # of cycles

  • Hertz or cycles/s

• total energy is proportional to the amp and the frequency of the wave

  • longer the amp, more force

  • more frequency, more force

Relationship between Wavelength and Frequency

• inversely proportional

• shorter the wavelength, more time they pass

• Ex 1: what is the wavelength of red light with a frequency of 4.62 × 10¹⁴ _s-1_?

  • use wavelength times frequency and convert it to nm (assume speed of light)

Color

• the color of light is determined by its wavelength

  • or frequency

• White light is a mixture of all the colors of visible light

  • a spectrum

  • ROYGBIV

• When an object absorbs some of the wavelengths of white light and reflects other, it appears colored

  • the observed color is predominantly the colors reflected

Amp & Wavelength

• different wavelength different colors

• different amps, different brightness

The Electromagnetic Spectrum

• shorter wavelength (high frequency) light has hiigher energy

  • radio wave light has the lowest energy

  • Gamma ray light has the highest energy

• high-energy electromagnetic radiation can potentially damage biological molecules

  • ionizing radiation

Types of Electromagnetic Radiation

• Electromagnetic waves are classified by their wavelength

• as they increase in frequency, they increase in energy

Radio Signal Transmission

• AM - amplitude modification

• FM - frequency modification

Standing Waves

• not all waves are travelling waves

• standing waves remain constrained within some region of space

• standing waves play an important role in our understanding of the elctronic structure of atoms and molecules

2-D Waves

• vibrational patterns of a flat surface are ex of 2D standing waves

• for 2d standing waves, the nodes are lines of the surface

Interference

• the interaction between waves is called interference

• waves in phase - constructive interference

• waves out of phase - destructive interference

Diffraction

• when waves encounter an obstacle or opening in a barrier that is about the same size as the wavelength, they bend around it

• with the 2-slit interference, there is constructive and and destructive interference

  • shows the difference between wave and particle interference

• waves bend around an obstacle, particles do not

Blackbody Radiation

• sunlight consists of a range of broadly distributed wavelengths that form a continuous spectrum

• blackbody: convenient, ideal emitter that approximates the behavior of many materials when heated

  • ex: metal oven that can be heated to high temps

Ultraviolet Catastrophe

• maxima in blackbody curves shift to shorter wavelengths as the temp increases

• theoretical expressions as functions of temp fit the observed experimental blackbody curves well at longer wavelength

• but there were significant discrepancies at shorter wavelengths → uv catastrophe

Max Planck (physics??)

• derived a theoretical expression for blackbody radiation that fit the experimental observations exactly

• atoms vibrated at increasing frequencies (or decreasing wavelengths) as temp increases

• light energy was delivered to the atoms in packets called quanta or photons

• proportionality (planck’s) constant: 6.626 × 10^-34 J x s

• energy of a photon is directly proportional to its frequency

  • inversely proportional to its wavelength

Practice

• By wavelength (short to long)

  • gamma, uv, green light, red light, microwave

• By frequency (l to h)

  • mw, red light, green light, uv, gamma

Photoelectric Effect

Photoelectric Effect: metals emit electrons when a light shines on their surface

• light energy being transferred to the elctron

• if wavelength is made shorter, or the intensity is brighter, more electrons should be ejected

• if a dim light were used there would be a lag time before electrons were emitted

The Problem

• threshold frequency: min frequency needed before electrons would be ejected

• high-frequency light from a dim source w/o lag time

Ejected Electrons

• one photon at the threshold frequency gives the electrons just enough energy for it to escape the atom

  • binding energy

• shorter wavelength photon, the electron will absorb more energy than is necessary to escape

• excess energy become KE of the ejected electron

Spectra

• when atoms or molecules absorb energy, that energy is released as light energy

• when that light is passed through a prism, a pattern of particular wavelengths of light is seen that is unique to that type of atom or molecule

  • called emission spectrum

    • non-continuous

    • flame tests can identify the material

Line Spectra of Hydrogen

• Balmer was able to derive an empirical equation that related the 4 visible wavelengths of light emitted by hydrogen atoms to whole integers

Rydberg’s Spectrum Analysis

• Rydberg analyzed the spectrum of hydrogen from Balmer’s work and came up with a generalized empirical formula to predict all emission lines from hydrogen

  • n₁ < n₂

Rutherford’s Nuclear Model

• atom contains tiny dense center called nucleus

• volume of the nucleus is 1/10 trillionth volume of the atom

• nucleus is essentially the entire mass of the atom

• nucleus is positively charged

• the positive charge is balanced with the negative charge of the electrons

• electrons move around in the empty space of the atom surrounding the nucleus

Problems w/ Rutherford’s Model

• electrons are moving charged particles

• moving charged particles give off energy

• therefore, electrons should constatnly give off energy

Bohr’s Model

• nuclear model doesn’t explain the structural changes when an atom gains or loses energy

• electrons travel in orbits that are a fixed distance from the nucleus

• electrons emit radiation when they “jump” from an orbit with higher energy down to an orbit with lower energy

• Bohr’s major idea was that the energy of the atom was quantized, and that the amount of energy in the atom was related to the electron’s position in the atom.

  • Quantized means that the atom could only have very specific amounts of energy

Quantum Explanation of Atomic Spectra

• each wavelength in the spectrum corresponds to an electron transition between orbitals

• when excited, electrons transition from an orbital of lower energy to one of higher energy

• when relaxed, transitions from a higher to a lower energy level

  • releases a photon of light whose energy equals the energy difference between orbitals

Electron Transitions

• electron must gain correct amount of energy to the difference in energy between the final and initial states

Predicting the Spectrum of Hydrogen

• wavelengths of lines in the emission spectrum of hydrogen can be predicted by calculating the difference in energy between any two states

• electrons in energy state n, there are (n – 1) energy states it can transition to, therefore (n – 1) lines it can generate.

• used for one-electron system

Energy Transitions in Hydrogen

• energy of a photon released is equal to the difference in energy between the 2 levels the electron is jumping between

• calculated by subtracting the energy of the initial state from the energy of the final state

Wave Behavior of Electrons

• de Broglie predicted that the wavelength of a particle is inversely proportional to its momentum

• b/c its so small, the wave character of electrons is significant

Electron Diffraction

• proof that the electron had wave nature came from the demonstration that a beam of electrons would produce an interference pattern as waves do

Uncertainty Principle

• Heisenberg determined the fundamental limit to how accurately a particle’s position and momentum can be measured simultaneously

• the more accurately the momentum is measured, the less accurately we can determine the position at that time and vice versa

• Heisenberg Uncertainty Principle: It is fundamentally impossible to determine simultaneously and exactly both the momentum and the position of a particle.

Complementary Properties

• when you try to observe the wave nature of the electron, you cannot observe its particle nature and vice-versa

  • wave nature = interference pattern

  • particle nature = position, which slit its passing through

• wave and particle nature of the electron are complementary

  • as you know more about one, you know less about the other

Determinacy vs. Indeterminacy

• particles move in a path determined by the particle’s velocity, position and forces acting on it

  • determinacy = definite, predictable future

• since we can’t know both the position and velocity of an electron, we cannot predict the path it will follow

  • indeterminacy = indefinite future, can only predict probability

• best we can do: describe the probability an electron will be found in a particular region using stats

Electron Energy

• Electron energy and position are complementary since KE = ½mv2

• best we can do: describe a region in the atom of high probability of finding it

• Many of the properties of atoms are related to the energies of the electrons

  • like ionization energy, metallic energy

Schrödinger’s Equation

• allows us to calculate the probability of finding an electron with a particular amount of energy at a particular location in the atom

• Ĥ is the Hamiltonian operator, a set of mathematical operations representing the total energy of the quantum particle

• ψ is the wavefunction of the particle

• E is the total energy of the particle

• Solutions to Schrödinger’s Equation produce many wave functions, ψ

• A plot of distance vs. ψ2 represents an orbital, a probability distribution map of a region where the electron is likely to be found

Solutions to the Wave Function, ψ

• shows the size, shape and orientation in space of an orbital are determined by 3 integer terms in the wave function called quantum numbers

  • principal quantum number, n (describes the size and energy of the orbital)

  • angular momentum quantum number, l (describes shape)

  • orientation quantum number, m_l (describes orientation)

  • magnetic spin quantum number, m_s (not an integer)

Principal Quantum Number, n

• Characterizes the energy of the electron in a particular orbital

  • pertaining to Bohr’s energy level

• n can be any inter >= 1

• The larger the value of n, the more energy the orbital has

• Energies are defined as being negative

  • An electron would have E = 0 when it just escapes the atom

• The larger the value of n, the larger the orbital.

• As n gets larger, the amount of energy between orbitals becomes smaller

Angular Momentum Quantum Number, l

• determines the shape of each value of l is called by the orbital

• a particular letter that designates the shape of the orbital

  • s orbitals are spherical (l = 0)

  • p orbitals are like two balloons tied at the knots (l = 1)

  • d orbitals are mainly like four balloons tied at the knot (l = 2)

  • f orbitals are mainly like eight balloons tied at the knot (l = 3)

Orientation Quantum Number, m_l

• specifies the orientation of the orbital

  • the direction in space the orbital is aligned relative to the other orbitals

• Values are integers from −l to +l

  • including zero

  • gives the number of orbitals of a particular shape

    • when l = 2, the values of ml are −2, −1, 0, +1, +2; which means there are five orbitals with l = 2

Magnetic Spin Quantum Number, m_s

• indicates the spin of electrons in the orbital

  • has a value +1/2 or -1/2

• Paramagnetic (has unpaired electrons)

  • substance is attracted to a magnetic field

  • substances with unpaired electrons are paramagnetic

• Diamagnetic (has no unpaired electrons)

  • NOT attracted to a magnetic field

  • Substances have paired spins

Describing an Orbital

• Each set of n, l, m_l , and m_s describes one orbital

• Orbitals with the same value of n are in the same principal energy level

  • or principal shell

• Orbitals with the same values of n and l are said to be in the same sublevel.

  • or subshell

Predicting Quantum Numbers

Determine a set of quantum numbers for an electron in a 3p orbital

n =3 for an electron in the third level

( n = 3, p = 1, l = -1, m_s = -1/2)

(n = 3, p = 1, l = -1, m_s = +1/2)

( n = 3, p = 1, l = 0, m_s = -1/2)

( n = 3, p = 1, l = 0, m_s = +1/2)

( n = 3, p = 1, l = 1, m_s = -1/2)

( n = 3, p = 1, l = 1, m_s = +1/2)

Probability & Radial Distribution Functions

• y² is the probability density

  • represents the total probability of finding an electron at a particular point in space

  • for s orbital maximum at the nucleus?

  • decreases as you move away from the nucleus

• The Radial Distribution function represents the total probability of finding an electron within a thin spherical shell at a distance r from the nucleus..

  • the probability at a point decreases with increasing distance from the nucleus, but the volume of the spherical shell increases

• Nodes in the functions are where the probability drops to 0

The Shapes of Atomic Orbitals

• The l quantum number primarily determines the shape of the orbital.

• l can have integer values from 0 to (n – 1).

• Each value of l is called by a particular letter that designates the shape of the orbital.

  • s orbitals are spherical.

  • p orbitals are like two balloons tied at the knots.

  • d orbitals are mainly like four balloons tied at the knot.

  • f orbitals are mainly like eight balloons tied at the knot.

  • know s and p orbitals and be able to recognize the d orbitals

l = 0, the s Orbital

• Each principal energy level has one s orbital.

• Lowest energy orbital in a principal energy state

• Spherical

• Number of nodes = (n – 1)

l = 1, p Orbitals

• Each principal energy state above n = 1 has three p orbitals.

  • m_l = −1, 0, +1

• Each of the three orbitals points along a different axis

  • p_x , p_y , p_z

• 2nd lowest energy orbitals in a principal energy state

• Two-lobed

• One node at the nucleus, total of n nodes

l = 2, d Orbitals

• Each principal energy state above n = 2 has five d orbitals.

  • m_l = −2, − 1, 0, +1, +2

• Four of the five orbitals are aligned in a different plane.

  • the fifth is aligned with the z axis, d_z²

  • d_xy, d_yz, d_xz d_{x² - y²}

• 3rd lowest energy orbitals in a principal energy level

• Mainly four-lobed

  • one is two-lobed with a toroid

• Planar nodes

  • higher principal levels also have spherical nodes

l = 3, f Orbitals

• Each principal energy state above n = 3 has seven f orbitals.

  • m_l = −3, −2, −1, 0, +1, +2, +3

• 4th lowest energy orbitals in a principal energy state

• Mainly eight-lobed

  • some two-lobed with a toroid

• Planar nodes

  • higher principal levels also have spherical nodes.

Periodicity – Periodic Table and Its Trends

History of the Periodic Table

• In 1669, Hennig Brand attempted to make a Philosopher’s Stone

• In 1680, Robert Boyle discovered phosphorus

• in 1863, John Newlands divided and then discovered 56 elements into 11 groups based on characteristics

• In 1897, English physicist J. J. Thomson first discovered electrons; small negatively charged particles in an atom. John Townsend and Robert Millikan determined their exact charge and mass. In 1900, Bequerel discovered that electrons and beta particles as identified by the Curies are the same thing.

• In 1903, Rutherford announced that radioactivity is caused by the breakdown of atoms.In 1911, Rutherford and German physicist Hans Geiger discovered that electrons orbit the nucleus of an atom.

• In 1913, Bohr discovered that electrons move around a nucleus in discrete energy called orbitals. Radiation is emitted during movement from one orbital to another.

Dimitri Mendeleev

• Order elements by atomic mass

• Observed a repeating pattern of properties

• Periodic Law: when the elements are arranged in order of increasing atomic mass, certain sets of properties recur periodically

• Put elements with similar properties in the same column

• Used pattern to predict properties of undiscovered elements

Electron Configurations

• Quantum-mechanical theory describes the behavior of electrons in atoms.

• The electrons in atoms exist in orbitals.

• A description of the orbitals occupied by electrons is called an electron configuration.

How Electrons Occupy Orbitals

• Calculations with Schrödinger’s equation show hydrogen’s one electron occupies the lowest energy orbital in the atom.

• Schrödinger’s equation calculations for multielectron atoms cannot be exactly solved.

  • due to additional terms added for electron-electron interactions

• Approximate solutions show the orbitals to be hydrogen-like.

• Two additional concepts affect multielectron atoms: electron spin and energy splitting of sublevels.

Electron Spin

• Experiments by Stern and Gerlach showed a beam of silver atoms is split in two by a magnetic field.

• The experiment reveals that the electrons spin on their axis.

• As they spin, they generate a magnetic field.

  • spinning charged particles generate a magnetic field.

• If there is an even number of electrons, about half the atoms will have a net magnetic field pointing “north” and the other half will have a net magnetic field pointing “south”.

The Property of Electron Spin

• Spin is a fundamental property of all electrons.

• All electrons have the same amount of spin.

• The orientation of the electron spin is quantized, it can only be in one direction or its opposite.

  • spin up or spin down

• The electron’s spin adds a fourth quantum number to the description of electrons in an atom, called the Spin Quantum Number, m_s.

Spin Quantum Number, m_s, and Orbital Diagrams

• m_s can have values of +½ or −½

• Orbital Diagrams use a square to represent each orbital and a half-arrow to represent each electron in the orbital

• A half-arrow pointing up is used to represent an electron in an orbital with spin up

• Spins must cancel in an orbital

  • paired

• We often represent an orbital as a square and the electrons in that orbital as arrows.

  • the direction of the arrow represents the spin of the electron.

Pauli Exclusion Principle

• No two electrons in an atom may have the same set of four quantum numbers.

• Therefore no orbital may have more than two electrons, and they must have with opposite spins.

• Knowing the number orbitals in a sublevel allows us to determine the maximum number of electrons in the sublevel.

  • s sublevel has 1 orbital, therefore, it can hold 2 total electrons.

  • p sublevel has 3 orbitals, therefore, it can hold 6 total electrons.

  • d sublevel has 5 orbitals, therefore, it can hold 10 total electrons.

  • f sublevel has 7 orbitals, therefore, it can hold 14 total electrons.

Quantum Numbers of Helium’s Electrons

• Helium has two electrons

• both electrons are in the first energy level.

• Both electrons are in the s orbital of the first energy level.

• Because they are in the same orbital, they must have opposite spins.

• first electron: n = 1, l = 0, m_l = 0, m^_s = +1/2

• second electron: n = 1, l = 0, m_l = 0, m_s = -1/2

Sublevel Splitting in Multielectron Atoms

• The sublevels in each principal energy shell of Hydrogen all have the same energy.

  • or other single electron systems

• Orbitals with the same energy - Degenerate

• For multielectron atoms, the energies of the sublevels are split.

  • caused by charge interaction, shielding and penetration

• The lower the value of the l quantum number, the less energy the sublevel has

Coulomb’s Law

• Coulomb’s Law describes the attractions and repulsions between charged particles.

• For like charges, the potential energy (E) is positive and decreases as the particles get farther apart .

• For opposite charges, the potential energy is negative and becomes more negative as the particles get closer together.

• The strength of the interaction increases as the size of the charges increases.

  • Electrons are more strongly attracted to a nucleus with a 2+ charge than a nucleus with a 1+ charge.

Effective Nuclear Charge

• In a particle (atom or ion) with more than one electron, there are both repulsions (between electrons) and attractions (between electrons and nucleus) to consider.

• The net positive charge from the nucleus that an electron experiences is the effective nuclear charge, Zeff.

• A valence electron experiences a Zeff that is lower than the actual nuclear charge, Z (number of protons). 𝑍eff<𝑍

• Some of the nuclear charge is shielded by the core (inner) electrons.

• 𝑍eff=𝑍−𝑆, where S is the shielding.

Shielding of Nuclear Charge

• Sodium has 1 valence electron in the 3s orbital and 10 core electrons, shielding it from the +11 charge of the nucleus.

  • has an overall charge of +1 since 11 - 10

• Magnesium has 2 valence electrons in the 3s orbital and the same 10 core electrons, shielding them from the +12 charge of the nucleus.

  • has an overall charge of +2 since 12 - 10

• Each valence electron shields the other to a small extent, but core electrons are more effective at shielding than valence electrons.

• Therefore, magnesium experiences a higher Zeff than sodium

**Slater’s Rules for Calculating Shielding, S**

• Valence electrons (in n energy level) contribute a value of 0.35 toward the shielding.

• Core or inner electrons (in any energy level less than n) contribute a value of 0.85 toward the shielding.

• 𝑆 = # valence electrons (0.35) + # core electrons (0.85)

• For sodium :

  • Z (amt of protons) = 11

  • S= 0(.35) + 10(.85) = 8.5

  • Z_eff = Z - S = 11 - 8.5 = +2.5

• having a higher effective nuclear charge makes it easier to take valence electrons away from an atom

Penetration

• The closer an electron is to the nucleus, the more attraction it experiences.

• The better an outer electron is at penetrating through the electron cloud of inner electrons, the more attraction it will have for the nucleus.

• The degree of penetration is related to the orbital’s radial distribution function.

  • In particular, the distance the maxima of the function are from the nucleus.

Penetration and Shielding

• The radial distribution function shows that the 2s orbital penetrates more deeply into the 1s orbital than does the 2p.

• The weaker penetration of the 2p sublevel means that electrons in the 2p sublevel experience more repulsive force, they are more shielded from the attractive force of the nucleus.

• The deeper penetration of the 2s electrons means electrons in the 2s sublevel experience a greater attractive force to the nucleus and are not shielded as effectively.

Effect of Penetration and Shielding

• Penetration causes the energies of sublevels in the same principal level to not be degenerate.

• In the fourth and fifth principal levels, the effects of penetration become so important that the s orbital actually lies lower in energy than the d orbitals of the previous principal level.

• The energy separations between one set of orbitals and the next become smaller beyond the 4s.

• The ordering can therefore vary among elements.

  • causing variations in the electron configurations of the transition metals and their ions

Rules in Filling in the Orbitals

• Energy levels and sublevels fill from lowest energy to highest.

  • s → p → d → f

  • Aufbau Principle

• Orbitals that are in the same sublevel have the same energy.

• No more than two electrons per orbital

  • Pauli Exclusion Principle

• When filling orbitals that have the same energy, place one electron in each before completing pairs.

  • Hund’s Rule

Ground State Electron Configuration

• The electron configuration is a listing of the sublevels in order of filling with the number of electrons in that sublevel written as a superscript.

  • Kr = 36 electrons = 1s22s22p63s23p64s23d104p6

• A short-hand way of writing an electron configuration is to use the symbol of the previous noble gas in [ ] to represent all the inner electrons, then just write the last set.

  • Rb = [Kr]5s1

Order of Sublevel Filling

• Start by drawing a diagram putting each energy shell on a row and listing the sublevels, (s, p, d, f), for that shell in order of energy (left-to right).

• Next, draw arrows through the diagonals, looping back to the next diagonal each time

• ex: Mn 1s²2s²2p⁶3s²3p⁶4s²3d⁵

• practice: full ground state orbital diagram and electron configuration of potassium

  • 1s²2s²2p⁶3s²3p⁶4s¹

Valence Electrons

• The electrons in all the sublevels with the highest principal energy shell are called the valence electrons.

• Electrons in lower energy shells are called core electrons.

• Chemists have observed that one of the most important factors in the way an atom behaves, both chemically and physically, is the number of valence electrons.

Electron Configuration & the Periodic Table

• The Group number corresponds to the number of valence electrons.

• The length of each “block” is the maximum number of electrons the sublevel can hold.

• The Period number corresponds to the principal energy level of the valence electrons.

Transition Elements

• For the d block metals, the principal energy level is one less than valence shell.

  • one less than the Period number

  • sometimes s electrons are “promoted” to d sublevel

• For the f block metals, the principal energy level is two less than valence shell.

  • two less than the Period number they really belong to

  • sometimes d electron in configuration

Irregular Electron Configurations

• Because of sublevel splitting, the 4s sublevel is lower in energy than the 3d; and therefore the 4s fills before the 3d.

  • ex: Cr = [Ar] 4s¹3d⁵

  • Cu = [Ar] 4s¹3d¹⁰

  • Mo = [Kr] 5s¹4d⁵

  • Ru = [Kr] 5s¹4d⁷

  • Pd = [Kr] 5s⁰4d¹⁰

• However, the difference in energy small.

• Some of the transition metals have irregular electron configurations in which the ns only partially fills before the (n−1)d or doesn’t fill at all.

• Therefore, their electron configuration must be found experimentally.

Properties & Electron Configuration

• The properties of the elements follow a periodic pattern.

  • Elements in the same column have similar properties.

  • Elements in a period show a pattern that repeats.

• The quantum-mechanical model explains this because the number of valence electrons and the types of orbitals they occupy are also periodic.

The Noble Gas Electron Configuration

• The noble gases have eight valence electrons.

  • except for He, which has only two electrons

• The noble gases are especially non-reactive.

  • He and Ne are practically inert

• The reason the noble gases are so non-reactive is that the electron configuration of the noble gases is especially stable

• ex: Na : [Ne] 3s¹ (one unpaired e- so it is paramagnetic)

• ex: Te : [Kr] 5s²4d¹⁰5p⁴ (2 unpaired e- so paramagnetic)

• ex: Tc : [Kr] 5s²4d⁵ (5 unpaired e- so paramagnetic)

The Alkali Metals

• The alkali metals have one more electron than the previous noble gas.

• In their reactions, the alkali metals tend to lose one electron, resulting in the same electron configuration as a noble gas.

  • forming a cation with a 1+ charge

The Halogens

• The electron configurations of the halogens all have one fewer electron than the next noble gas.

• In their reactions with metals, the halogens tend to gain an electron and attain the electron configuration of the next noble gas.

  • forming an anion with charge 1−

• In their reactions with nonmetals, they tend to share electrons with the other nonmetal so that each attains the electron configuration of a noble gas.

Eight Valence Electrons

• Quantum mechanical calculations show that eight valence electrons should result in a very unreactive atom.

  • an atom that is very stable

  • Noble gases have eight valence electrons and are all very stable and unreactive.

    • Note:  Helium only has two valence electrons, but that fills its valence shell.

• Conversely, elements that have either one more or one less electron should be very reactive.

  • Halogen atoms have seven valence electrons and are, in general, the most reactive nonmetals .

  • Alkali metals have one more electron than a noble gas atom and are, in general, the most reactive metals

Electron Configuration & Ion Charge

• Many metals and nonmetals form one ion, and that the charge on that ion is predictable based on its position on the Periodic Table.

  • Group 1A = 1+

  • Group 2A = 2+

  • Group 7A = 1−

  • Group 6A = 2−

  • etc.

• These atoms form ions that will result in an electron configuration that is the same as the nearest noble gas.

• they are isoelectronic to their closest noble gases

Ground State Electronic Configuration of Anions

• Anions are formed when nonmetal atoms gain enough electrons to have eight valence electrons.

  • filling the s and p sublevels of the valence shell

• The sulfur atom has six valence electrons.

  • S atom = 1s²2s²2p⁶3s²3p⁴

• In order to have eight valence electrons, sulfur must gain two more.

  • S^2- anion = 1s²2s²2p⁶3s²3p⁶

Ground State Electronic Configuration of Cations

• Cations are formed when a metal atom loses all its valence electrons.

  • This results in a new lower energy level valence shell.

  • However, the process is always endothermic.

• The magnesium atom has two valence electrons.

  • Mg atom = 1s²2s²2p⁶3s²

• When magnesium forms a cation, it loses its valence electrons to produce a stable noble-gas configuration.

  • Mg²⁺ cation = 1s²2s²2p⁶

Trend in Atomic Radius - Main Group

• There are several methods for measuring the radius of an atom, and they give slightly different numbers.

  • van der Waals radius = nonbonding

  • covalent radius = bonding radius

  • Atomic radius is an average radius of an atom based on measuring large numbers of elements and compounds.

• Atomic Radius increases down a group.

  • The valence shell is farther from the nucleus.

  • Effective nuclear charge is fairly close.

• Atomic Radius decreases across period (left to right).

  • Electrons are added to the same valence shell.

  • Effective nuclear charge increases.

  • The valence shell is held closer by the nucleus.

Quantum-Mechanical Explanation for the Group Trend in Atomic Radius

• The size of an atom is related to the distance the valence electrons are from the nucleus.

• the larger the orbital an electron is in, the farther its most probable distance will be from the nucleus and the less attraction it will have for the nucleus.

• Traversing down a group adds a principal energy level.

• The larger the principal energy level an orbital is in, the larger its volume.

• therefore, quantum-mechanics predicts the atoms should get larger down a column.

Quantum-Mechanical Explanation for the Period Trend in Atomic Radius

• The larger the effective nuclear charge an electron experiences, the stronger the attraction it will have for the nucleus.

• The stronger the attraction the valence electrons have for the nucleus, the closer their average distance will be to the nucleus.

• Traversing across a period increases the effective nuclear charge on the valence electrons.

• therefore, quantum-mechanics predicts the atoms should get smaller across a period.

Trends in Atomic Radius - Transition Metals

• Atoms in the same group increase in size down the column.

• Atomic radii of transition metals roughly the same size across the d block.

  • much less difference than across main group elements

  • valence shell ns2, not the (n−1)d electrons

  • effective nuclear charge on the ns2 electrons approximately the same

Electron Configurations of Main Group Cations

• Cations form when the atom loses electrons from the valence shell.

Electron Configurations of Transition Metal Cations

• When transition metals form cations, the first electrons removed are the valence electrons, even though other electrons were added after.

• Electrons may also be removed from the sublevel closest to the valence shell after the valence electrons.

• The iron atom has two valence electrons.

  • Fe atom = 1s²2s²2p⁶3s²3p⁶4s²3d⁶

• When iron forms a cation, it first loses its valence electrons.

  • Fe2+ cation = 1s²2s²2p⁶3s²3p⁶3d⁶

• It can then lose 3d electrons.

  • Fe3+ cation = 1s²2s²2p⁶3s²3p⁶3d⁵

Magnetic Properties of Transition Metal Atoms & Ions

• Electron configurations that result in unpaired electrons mean that the atom or ion will have a net magnetic field – this is called paramagnetism.

  • will be attracted to a magnetic field

• Electron configurations that result in all paired electrons mean that the atom or ion will have no magnetic field – this is called diamagnetism.

  • slightly repelled by a magnetic field

Transition Metal Atoms and Ions: Electron Configuration & Magnetic Properties

• Both Zn atoms and Zn²⁺ ions are diamagnetic.

  • showing that the two 4s electrons are lost before the 3d

  • Zn atoms [Ar]4s²3d¹⁰

  • Zn2+ ions [Ar]4s⁰3d¹⁰

• Ag forms both Ag⁺ ions and, rarely, Ag²⁺.

  • Ag atoms [Kr]5s¹4d¹⁰ are paramagnetic

  • Ag+ ions [Kr]4d¹⁰ are diamagnetic

  • Ag2+ ions [Kr]4d⁹ are paramagnetic

Trends in Ionic Radius

• Ions in same group have same charge.

• Ion size increases down the column.

  • higher valence shell, larger

• Cations are smaller than neutral atoms.

• Anions are larger than neutral atoms.

• Cations are smaller than anions.

  • except Rb+ & Cs+ bigger or same size as F− and O2−

• Larger positive charge = smaller cation

  • for isoelectronic species

  • isoelectronic = same electron configuration

• Larger negative charge = larger anion

  • for isoelectronic species

Quantum-Mechanical Explanation for the Trends in Cation Radius

• When atoms form cations, the valence electrons are removed.

• The farthest electrons from the nucleus then are the p or d electrons in the (n − 1) energy level.

• This results in the cation being smaller than the atom.

• These “new valence electrons” also experience a larger effective nuclear charge than the “old valence electrons,” shrinking the ion even more.

• Traversing down a group increases the (n − 1) level, causing the cations to get larger.

• Traversing to the right across a period increases the effective nuclear charge for isoelectronic cations, causing the cations to get smaller.

Quantum-Mechanical Explanation for the Trends in Anion Radius

• When atoms form anions, electrons are added to the valence shell.

• These “new valence electrons” experience a smaller effective nuclear charge than the “old valence electrons,” increasing the size.

• The result is that the anion is larger than the atom.

• Traversing down a group increases the n level, causing the anions to get larger.

• Traversing to the right across a period increases the effective nuclear charge for isoelectronic anions, causing the anions to get smaller.

Ionization Energy

• Minimum energy needed to remove the outmost electron from an atom or ion

  • gas state

  • endothermic process

  • valence electron easiest to remove, lowest IE

  • M(g) + IE₁ → M¹⁺(g) + 1 e-

  • M¹⁺(g) + IE₂ → M²⁺(g) + 1 e-

• 1st ionization energy (IE) = energy to remove electron from neutral atom

• 2nd IE = energy to remove from 1+ ion; etc.

General Trends in 1st Ionization Energy

• The larger the effective nuclear charge on the electron, the more energy it takes to remove it.

• The farther the most probable distance the electron is from the nucleus, the less energy it takes to remove it.

• 1st IE decreases down the group.

  • The valence electron is farther from the nucleus.

• 1st IE generally increases across the period.

  • Effective nuclear charge increases.

  • doesn’t change much for transition elements since they all have the same amounts of valence electrons

Quantum-Mechanical Explanation for the Trends in First Ionization Energy

• The strength of attraction is related to the most probable distance the valence electrons are from the nucleus and the effective nuclear charge the valence electrons experience.

• The larger the orbital an electron is in, the farther its most probable distance will be from the nucleus and the less attraction it will have for the nucleus

• therefore quantum-mechanics predicts the atom’s first ionization energy should get lower down a column.

• Traversing across a period increases the effective nuclear charge on the valence electrons.

• therefore quantum-mechanics predicts the atom’s first ionization energy should get larger across a period.

Exceptions in the 1st IE Trends

• generally increases from left to right across a period

• except from 2A to 3A, 5A to 6A

  • To ionize beryllium, a full sublevel must be broken up, resulting in extra energy

  • When boron is ionized, a full sublevel is the formed, resulting in less energy

  • To ionize nitrogen, a half-full sublevel must be broken up, resulting in extra energy

  • When oxygen is ionized, a half-full sublevel is formed, resulting in less energy

Trends in Successive Ionization Energies

• Removal of each successive electron costs more energy

  • Shrinkage in size is due to having more protons than electrons

  • Outer electrons are closer to the nucleus; therefore, they are harder to remove

• Regular increase in energy for each successive valence electron

• Large increase in energy when start removing core electrons

Second and Third Ionization Energies

• The second ionization energy of an atom is the energy required to remove the second electron from the +1 gaseous ion.

• The third ionization energy is the energy required to remove the third electron from the +2 ion.

Electron Affinity

• Energy is released when an neutral atom gains an electron

  • gas state

  • M(g) + 1 e- → M^1-(g) + EA

• EA is defined as exothermic (−), but may actually be endothermic (+).

  • Some alkali earth metals & all noble gases are endothermic. Why?

• The more energy that is released, the larger the electron affinity.

  • the more negative the number, the larger the EA

Trends in Electron Affinity

• Alkali metals decrease electron affinity down the column.

  • but not all groups do

  • generally irregular increase in EA from 2nd period to 3rd period

• “Generally” increases across period

  • becomes more negative from left to right

  • not absolute

  • Group 5A generally lower EA than expected because extra electron must pair

  • Group 2A and 8A generally very low EA because added electron goes into higher energy level or sublevel

• Highest EA in any period = halogen

Properties of Metals & Nonmetals

• Metals

  • malleable & ductile

  • shiny, lusterous, reflect light

  • conduct heat and electricity

  • most oxides basic and ionic

  • form cations in solution

  • lose electrons in reactions – oxidized

• Nonmetals

  • brittle in solid state

  • dull, non-reflective solid surface

  • electrical and thermal insulators

  • most oxides are acidic and molecular

  • form anions and polyatomic anions

  • gain electrons in reactions – reduced

Metallic Character

• Metallic character is how closely an element’s properties match the ideal properties of a metal

  • more malleable and ductile, better conductors, and easier to ionize

• Metallic character decreases left-to-right across a period

  • metals are found at the left of the period and nonmetals are to the right

• Metallic character increases down the column

  • nonmetals are found at the top of the middle Main Group elements and metals are found at the bottom

Quantum-Mechanical Explanation for the Trends in Metallic Character

• Metals generally have smaller first ionization energies and nonmetals generally have larger electron affinities.

  • except for the noble gases

• therefore, quantum-mechanics predicts the atom’s metallic character should increase down a column because the valence electrons are not held as strongly

• therefore, quantum-mechanics predicts the atom’s metallic character should decrease across a period because the valence electrons are held more strongly and the electron affinity increases.

Chemical Bonding and Lewis Structures

Bonding Theories

• Explain how and why atoms attach together to form molecules.

• Explain why some combinations of atoms are stable and others are not.

  • why is water H₂O, not HO or H₃O

• Use to predict the shapes of molecules.

• Use to predict the chemical and physical properties of compounds.

Lewis Bonding Theory

• One of the simplest bonding theories is called Lewis Theory

• Lewis Theory emphasizes valence electrons to explain bonding

• Using Lewis theory, models can be drawn based on Lewis structures.

  • aka Electron Dot Structures

• Many properties of molecules can be predicted by using Lewis structures.

  • such as molecular stability, shape, size, polarity

Why Do Atoms Bond?

• Chemical bonds form because they lower the potential energy between the charged particles that make up the atoms.

• A chemical bond forms when the potential energy of the bonded atoms is less than the potential energy of the separate atoms.

• To calculate this potential energy, the following interactions need to be considered:

  • nucleus–to–nucleus repulsions

  • electron–to–electron repulsions

  • nucleus–to–electron attractions

Ionic Bonds

• When a metal atom loses electrons, it becomes a cation.

• Metals have low ionization energies, making it relatively easy to remove electrons from them.

• When a nonmetal atom gains electrons, it becomes an anion.

  • Nonmetals have high electron affinities, making it advantageous to add electrons to these atoms.

• The oppositely charged ions are then attracted to each other, resulting in an ionic bond. Ionic bonds are electrostatic in nature.

Covalent Bonds

• Nonmetal atoms have relatively high ionization energies, so it is difficult to remove electrons from them.

• When nonmetals bond together, it is better in terms of potential energy for the atoms to share valence electrons.

  • Potential energy is lowest when the electrons are between the nuclei.

• Shared electrons hold the atoms together by attracting nuclei of both atoms

Metallic Bonds

• The relatively low ionization energy of metals allows them to lose electrons easily.

• The simplest theory of metallic bonding involves the metal atoms releasing their valence electrons to be shared as a pool by all the atoms/ions in the metal.

  • It resembles an organization of metal cation islands that are separated in a sea of electrons.

  • Electrons are delocalized throughout the metal structure.

• Bonding results from attraction of cation for the delocalized electrons

Valence Electrons & Bonding

• Valence electrons are held most loosely.

• Chemical bonding involves the transfer or sharing of electrons between two or more atoms.

• Valence electrons are most important in bonding.

• Lewis theory focuses on the behavior of the valence electrons

Determining the Number of Valence Electrons in an Atom

• the column number on the periodic table indicates how many valence electrons a main group atom has

  • most transition elements have 2 valence electrons

Lewis Structures of Atoms

• in a Lewis structure, the valence electrons of main-group elements are represented as dots surrounding the symbol for the element

  • aka electron dot structures

• the symbol of element is used to represent the nucleus and the inner electrons

• dots around the symbol are used to represent valence electrons

  • pair the first 2 dots for the s orbital electrons

  • put one dot on each open side for first three p electrons

  • pair the rest of dots for the remaining p electrons

Stable Electron Arrangement and Ion Change

• metals form cations by losing enough electrons to get the same electron configuration as the previous noble gas

• nonmetals form anions by gaining enough electrons to get the same electron configuration as the next noble gas

• the noble gas electron configuration must be very stable

Lewis Bonding Theory

• atoms form bonds bc bonding results in a more stable electron config.

  • more stable = lower PE

• atoms bond tg by either transferring or sharing outer electrons

• this results in most atoms obtaining an outer shell with 8 electrons

  • octet rule

  • some exceptions

Octet Rule

• ns²np⁶

  • noble gas configuration

• exceptions:

  • H, Li, Be, B : attain an electron config like He

    • helium: two valence electrons, a duet

    • lithium: loses its one valence electron

    • hydrogen: shares or gains one electron

      • usually loses to become H⁺

    • beryllium: loses two electrons to become Be⁺

      • usually shares its 2 electrons in covalent bonds, resulting in 4 valence electrons

    • boron: loses 3 electrons to become B⁺

      • usually shares its 3 electrons in covalent bonds, resulting in 6 valence electrons

  • expanded octets: often occur for elements in period 3 or below

    • usually by empty valence d orbitals

Ionic Bonds

• when a metal loses electrons, it becomes a cation

  • metals have low ionization energies, making it easy to remove electrons from them

• when a nonmetal atom gains electrons it becomes an anion

  • nonmetals have high electron affinities, making it beneficial for them to add electrons to these atoms

• oppositely charged ions are attracted to each other, resulting in an ionic bond which are electrostatic in nature

Electron Transfer to Form Compounds

• metal atoms can transfer electrons to nonmetal atoms to form ions

• these ions attract each other due to opposite charges forming ionic bonds

• when forming ionic compounds, atoms tend to accept or donate electrons to achieve the electronic structure of the nearest noble gas

Ionic Lattice

• individual pairs of ions do not bond together, rather huge numbers of both types of ions form a 3D lattice

• the chemical formula of an ionic compound indicates the simplest ratio of the types of ions in the lattice

• the lattice is held together by electrostatic attraction s between the many oppositely charged cations and anions

  • very different from the bonding of discrete particles

Ionic Bonding and the Crystal Lattice

• the extra energy released comes from the formation of a strucutre in which every cation is surrounded by anions

  • called a crystal lattice

• held tg by electrostatic attractions of the cations for all surrounding anions

• c.l maximizes the attractions between cations and anions which leads to the most stable arrangement

Crystal Lattice

• electrostatic attraction is non-directional

  • no direct anion-cation pair

• therefore, there is no ionic molecule

  • the chemical formula is an empirical formula by giving the ratio of ions based on charge balance

Lattice Energy

• the extra stability that accompanies the formation of the crystal lattice is measured as the lattice energy

• the lattice energy is the energy released when the solid crystal forms from separate ions in the gaseous state

  • always exothermic

  • hard to measure directly, but can be calculated from knowledge of other process

  • born-haber cycle

• depends directly on size of charges and inversely on distance between ions

• ∆𝐸=1/(4𝜋𝜀_o ) (𝑞₁𝑞₂)/𝑟

Trends in Lattice Energy Ion Size

• force of attraction between charged particles is inversely proportional to the distance between them

• larger ions mean the center of positive charge (nucleus of the cation) is farther away form the negative charge (electrons of the anion)

  • larger ion = weaker attraction

  • weaker attraction = smaller lattice energy

Trends in Lattice Energy Ion charge

• the force of attraction between oppositely charged particles is directly proportional to the product of the charges

• larger charge means the ions are more strongly attracted to each other

  • larger charge = stronger attraction

  • stronger attraction = larger lattice energy

• of the two factors, charge is more important

Ionic Bonding: Model vs IRL

• Lewis theory implies that the attractions between ions are strong

• Lewis theory predicts ionic compounds should have high melting points and boiling points because breaking down the crystal should require a lot of energy

  • the stronger the attraction (larger the lattice energy), the higher the melting point

• Ionic compounds do have high melting points and boiling points

  • MP generally > 300 °C

  • All ionic compounds are solids at room temperature.

Covalent Bonding

Lewis Theory of Covalent Bonding

• implies that an alternative way atoms can achieve an octet of valence electrons is to share their valence electrons with other atoms

• the shared electrons would then count towards each atom’s octet

  • sharing of e- is covalent bonding

Covalent Bonding: Model vs Reality

• Lewis theory implies that some combinations should be stable, whereas others should not.

  • Because the stable combinations result in “octets”

• Using these ideas, Lewis theory allows us to predict the formulas of molecules of covalently bonded substances.

• Hydrogen and the halogens are all diatomic molecular elements, as predicted by Lewis theory.

• Oxygen generally forms either two single bonds or a double bond in its molecular compounds, as predicted by Lewis theory.

  • There are some stable compounds in which oxygen has one single bond and another where it has a triple bond, but it still has an octet.

• Lewis theory of covalent bonding implies that the attractions between atoms are directional.

• The shared electrons are most stable between the bonding atoms.

• Therefore, Lewis theory predicts that covalently bonded compounds will be found as individual molecules.

  • rather than an array like ionic compounds

• Compounds of nonmetals are made of individual molecule units.

• Lewis theory predicts the melting and boiling points of molecular compounds should be relatively low.

• It involves breaking the attractions between the molecules, but not the bonds between the atoms.

  • The covalent bonds are strong, but the attractions between the molecules are generally weak.

• Molecular compounds have low melting points and boiling points.

  • MP generally < 300 °C.

  • Molecular compounds are found in all three states at room temperature.

• Lewis theory predicts that the hardness and brittleness of molecular compounds should vary depending on the strength of intermolecular attractive forces.

  • The type and the strength of the intermolecular attractions vary based on many factors.

• Some molecular solids are brittle and hard, but many are soft and waxy.

• Lewis theory predicts that neither molecular solids nor liquids should conduct electricity.

  • There are no charged particles around to allow the material to conduct.

• Molecular compounds DO NOT conduct electricity in the solid or liquid state .

• Molecular acids conduct electricity when dissolved in water because they are IONIZED by water.

• Lewis theory predicts that the more electrons two atoms share, the stronger the bond should be.

• Bond strength is measured by how much energy must be added into the bond to break it in half.

• In general, triple bonds are stronger than double bonds, and double bonds are stronger than single bonds.

  • however, Lewis theory would predict double bonds are twice as strong as single bonds, but the reality is that they are less than twice as strong.

• Lewis theory predicts that the more electrons two atoms share, the shorter the bond should be.

  • when comparing bonds to like atoms

• Bond length is determined by measuring the distance between the nuclei of bonded atoms.

• In general, triple bonds are shorter than double bonds, and double bonds are shorter than single bonds.

Polar Covalent Bonding

• Covalent bonding between unlike atoms results in unequal sharing of the electrons.

  • One atom pulls the electrons in the bond closer to its side.

  • One end of the bond has larger electron density than the other.

• The result is a polar covalent bond.

  • bond polarity

  • The end with the larger electron density gets a partial negative charge.

  • The end that is electron deficient gets a partial positive charge.

Bond Polarity

• Most bonds have some degree of sharing and some degree of ion formation to them.

• Bonds are classified as covalent if the amount of electron transfer is insufficient (less than 50%) for the material to display the classic properties of ionic compounds.

• If the sharing is unequal enough to produce a dipole in the bond, the bond is classified as polar covalent.

Electronegativity

• The ability of an atom to attract bonding electrons to itself is called electronegativity.

• Increases across period (left to right).

• Decreases down group (top to bottom).

  • Fluorine is the MOST electronegative element.

  • Francium is the LEAST electronegative element.

  • Noble gas atoms are not assigned values.

  • Opposite of atomic size trend

• The larger the difference in electronegativity, the more polar the bond.

  • The negative end is toward the more electronegative atom.

The Effect of Delta EN on Bond Type

• Delta EN < .5 (non-polar covalent bond)

• .5 < Delta EN < 1.9 (polar covalent bond)

• Delta EN > 1.9 (ionic)

Bond Dipole Moments

• Dipole moment, m, is a measure of bond polarity.

  • A dipole is a material with a “+” and “−” end.

  • It is directly proportional to the size of the partial charges and directly proportional to the distance between them.

    • m = (q)(r)

    • not Coulomb’s Law

    • measured in Debyes, D

• Generally, the more electrons two atoms share and the larger the atoms are, the larger the dipole moment.

Percent Ionic Character

• The percent ionic character is the percentage of a bond’s measured dipole moment compared to what it would be if the electrons were completely transferred.

• The percent ionic character indicates the degree to which the electron is transferred.

Partial Charge on Dipole Moment

• If the % character is 50% or greater, the bond is considered ionic.

• If it is less than 50%, it is considered a polar covalent bond with a dipole moment.

• For example, if a diatomic molecule (XY) has a % ionic character of 15%. This indicates that the electron has been transferred 15% from X to Y.

• Therefore, the partial charge on elements X and Y would be

  

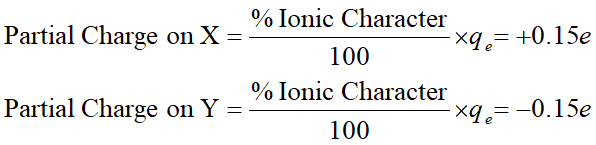
Lewis Structures of Molecules

• Lewis theory allows us to predict the distribution of valence electrons in a molecule.

• It is useful for the understanding the bonding in many compounds.

• Allows us to predict shapes of molecules.

• Allows us to predict properties of molecules and how they will interact together.

Lewis Structures

• In general, follow the common bonding patterns.

  • C = 4 bonds & 0 lone pairs; N = 3 bonds & 1 lone pair, O= 2 bonds & 2 lone pairs; H and halogen = 1 bond; Be = 2 bonds & 0 lone pairs; B = 3 bonds & 0 lone pairs

  • Lewis structures with line bonds often have the lone pairs left off.

    • Their presence is assumed from common bonding patterns.

• Structures that result in bonding patterns different from the common patterns may have formal charges.

Formal Charge

• The charge that is assigned to an atom in a molecule, assuming that electrons in all chemical bonds are shared equally between atoms, regardless of relative electronegativity.

• The BEST Lewis structure for a molecule is chosen such that the formal charge on each of the atoms is as close to zero as possible.

• FC = valence e− − nonbonding e− − ½ bonding e−

• Sum of all the formal charges in a molecule is zero.

  • In an ion, the total of the formal charges equals the overall charge.

Exceptions to the Octet Rule

• Expanded octets

  • Elements with empty d orbitals can have more than eight electrons.

• Odd number electron species e.g., NO

  • will have one unpaired electron

  • free-radical

  • very reactive

• Incomplete octets

  • B, Al

Resonance

• Lewis theory localizes the electrons between the atoms that are bonding together.

• Extensions of Lewis theory suggest that there is some degree of delocalization of the electrons – resonance.

• Delocalization of charge helps to stabilize the entire molecule

Resonance Structures

• When there is more than one Lewis structure for a molecule that differ only in the position of the electrons, they are called resonance structures.

• The actual molecule is a combination of the resonance forms – a resonance hybrid.

  • The molecule does not resonate between the two forms, even though we often draw it that way.

• Look for multiple bonds or lone pairs.

Rules of Resonance Structures

• Resonance structures must have the same connectivity.

  • Only electron positions can change.

• Resonance structures must have the same number of electrons.

• Second row elements have a maximum of eight electrons.

  • bonding and nonbonding

  • Third row can have expanded octet.

• Formal charges must total same.

Evaluating Resonance Structures

• Better structures have fewer formal charges.

• Better structures have smaller formal charges.

• Better structures have the negative formal charge on the more electronegative atom

Bond Energies

• Chemical reactions involve breaking bonds in reactant molecules and making new bonds to create the products.

• The delta H°reaction can be estimated by comparing the cost of breaking old bonds to the income from making new bonds.

• The amount of energy it takes to break one mole of a bond in a compound is called the bond energy.

  • in the gas state

  • each atom gets ½ bonding electrons

• bonds broken → endothermic reactions

• bonds formed → exothermic reactions

Trends in Bond Energies

• In general, the more electrons two atoms share, the stronger the covalent bond.

  • must be comparing bonds between like atoms

  • C≡C (837 kJ) > C=C (611 kJ) > C−C (347 kJ)

  • C≡N (891 kJ) > C=N (615 kJ) > C−N (305 kJ)

• In general, the shorter the covalent bond, the stronger the bond.

  • must be comparing similar types of bonds

  • Br−F (237 kJ) > Br−Cl (218 kJ) > Br−Br (193 kJ)

  • Bonds get weaker down the column.

  • Bonds get stronger across the period.

Bond Lengths

• The distance between the nuclei of bonded atoms is called the bond length.

• Because the actual bond length depends on the other atoms around the bond we often use the average bond length.

  • It is averaged for similar bonds from many compounds.

Shapes and Bonding Theories

Structure Determines Properties!

• Properties of molecular substances depend on the structure of the molecule.

• The structure includes many factors, such as:

  • the skeletal arrangement of the atoms

  • the kind of bonding between the atoms

    • ionic, polar covalent, or covalent

  • the shape of the molecule

• So far, Lewis dot structure only reveals electron sharing in two dimensions.

• Therefore, Lewis bonding theory needs to be modified in order to allow for the prediction of molecular shapes.

Molecular Geometry

• Molecules are 3-dimensional objects.

• The shapes of a molecule can be related to different geometric figures.

• These geometric shapes have characteristic “corners” that indicate the positions of the surrounding atoms around a central atom in the center of the geometric shape.

• The geometric figures also have characteristic angles -bond angles.

Lewis Theory Predicts Electron Groups

• Lewis theory predicts that there are different regions (domains) of electrons in an atom.

• Some regions result from placing shared pairs of valence electrons between bonding nuclei.

• Other regions result from placing unshared valence electrons on a single nuclei.

Using Lewis Theory to Predict Molecular Shapes

• Lewis theory says that these regions of electron groups/domains should repel each other.

• This idea can then be extended to predict the shapes of molecules.

  • The position of atoms surrounding the central atom will be determined by where the bonding electron groups are located – electron group geometry.

  • The positions of the electron groups will be determined by trying to minimize repulsions among them.

VSEPR Theory

• Electron groups around the central atom will be most stable when they are as far apart from each other as possible. This is called the Valence Shell Electron Pair Repulsion theory.

• Because electrons are negatively charged, they should be most stable when they are separated from each other as much as possible.

• The resulting geometric arrangement allows for the prediction of the shapes and bond angles in a molecule

Electron Groups/Domains

• Lewis dot structure predicts the number of valence electron pairs around the central atom(s) .

• Each lone pair of electrons constitutes one electron group on a central atom.

• Each bond constitutes one electron group on a central atom.

  • regardless of whether it is single, double, or triple!!!

Electron Group Geometry

• There are five basic arrangements of electron groups around a central atom.

  • based on a maximum of six bonding electron groups

• Each of these five basic arrangements results in five different basic electron geometries.

  • In order for the molecular shape and bond angles to be a “perfect” geometric figure, all the electron groups must be the same, bonded groups or lone pairs.

• For molecules that exhibit resonance, it doesn’t matter which resonance form you use – the electron geometry will be the same.

Linear Electron Geometry

• When there are two electron groups around the central atom, they will occupy positions on opposite sides of the central atom.

• This results in the electron groups taking a linear geometry.

• The bond angle is 180°.

Trigonal Planar Electron Geometry

• When there are three electron groups around the central atom, they will occupy positions in the shape of a triangle around the central atom.

• This results in the electron groups taking a trigonal planar geometry.

• The bond angle is 120°.

Tetrahedral Electron Geometry

• When there are four electron groups around the central atom, they will occupy positions in the shape of a tetrahedron around the central atom.

• This results in the electron groups taking a tetrahedral geometry.

• The bond angle is 109.5°.

Trigonal Bipyramidal Electron Geometry

• When there are five electron groups around the central atom, they will occupy positions in the shape of two tetrahedrals that are base-to-base with the central atom in the center of the shared bases.

• This results in the electron groups taking a trigonal bipyramidal geometry.

• The positions above and below the central atom are called the axial positions.

• The positions in the same base plane as the central atom are called the equatorial positions.

• The bond angle between equatorial positions is 120°.

• The bond angle between axial and equatorial positions is 90°.

• The bond angle between the two axial positions is 180°.

Octahedral Electron Geometry

• When there are six electron groups around the central atom, they will occupy positions in the shape of two square-base pyramids that are base-to-base with the central atom in the center of the shared bases.

• This results in the electron groups taking an octahedral geometry.

  • This is called octahedral because the geometric figure has eight sides.

• All corner positions are equivalent.

• The bond angle is 90°.

Molecular Geometry

• The actual geometry of the molecule may be different from the electron geometry.

• When the electron groups are attached to atoms of different size, or when the bonding to one atom is different than the bonding to another, this will affect the molecular geometry around the central atom.

• Lone pairs affect the molecular geometry tremendously.

  • They occupy space around the central atom, but are not “seen” as points on the molecular geometry.

The Effect of Lone Pairs

• Lone pair groups “occupy more space” on the central atom.

• since their electron density is exclusively on the central atom rather than shared like bonding electron groups

• Relative sizes of repulsive force interactions:

• Lone Pair – Lone Pair > Lone Pair – Bonding Pair > Bonding Pair – Bonding Pair

• This affects the bond angles, making the bonding pair – bonding pair angles smaller than expected if there are lone pair(s) around the central atom.

Bent Molecular Geometry/Shape: Derivative of Trigonal Planar Electron Geometry

• When there are three electron groups around the central atom, and one of them is a lone pair, the resulting shape of the molecule is called a trigonal planar — bent shape or trigonal bent.

• The bond angle is less than 120°.

Derivatives of the Tetrahedral Electron Geometry

• When there are four electron groups around the central atom, and some are lone pairs, they will occupy one or two of the characteristic corners in the tetrahedron.

• When there are four electron groups around the central atom, and one is a lone pair, the result is called the trigonal pyramidal.

• When there are four electron groups around the central atom, and two are lone pairs, the result is called the tetrahedral bent.

• The bond angles for both trigonal pyramidal and tetrahedral bent are less than 109.5° due to the larger repulsion for the lone pair(s).

Derivatives of the Trigonal Bipyramidal Electron Geometry

• When there are five electron groups around the central atom, and some are lone pairs, they will occupy the equatorial positions because there is more room.

• When there are five electron groups around the central atom, and one is a lone pair, the result is called the seesaw shape.

• When there are five electron groups around the central atom, and two are lone pairs, the result is called the T-shaped.

• When there are five electron groups around the central atom, and three are lone pairs, the result is a linear shape.

• The bond angles between equatorial positions are less than 120°

• The bond angles between axial and equatorial positions are less than 90°

  • linear = 180° axial–to–axial