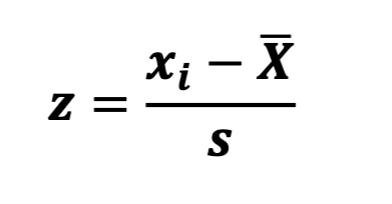Z Scores

what is a z score?

• Z SCORE: a measure of how far from the mean a data point is in units of standard deviations rather than in units of the original variable

  • 

  • very helpful for comparing across measures with different units of measurement

  • 

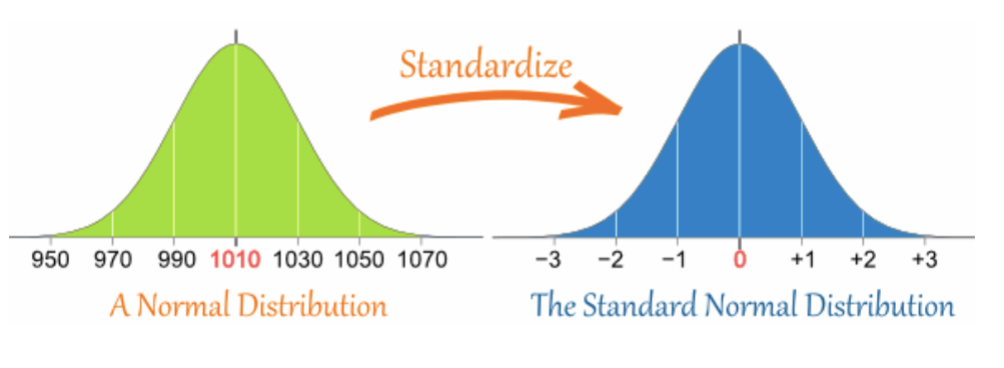
• STANDARD NORMAL CURVE: a theoretical normal distribution with a mean of zero and a standard deviation of 1

  • 

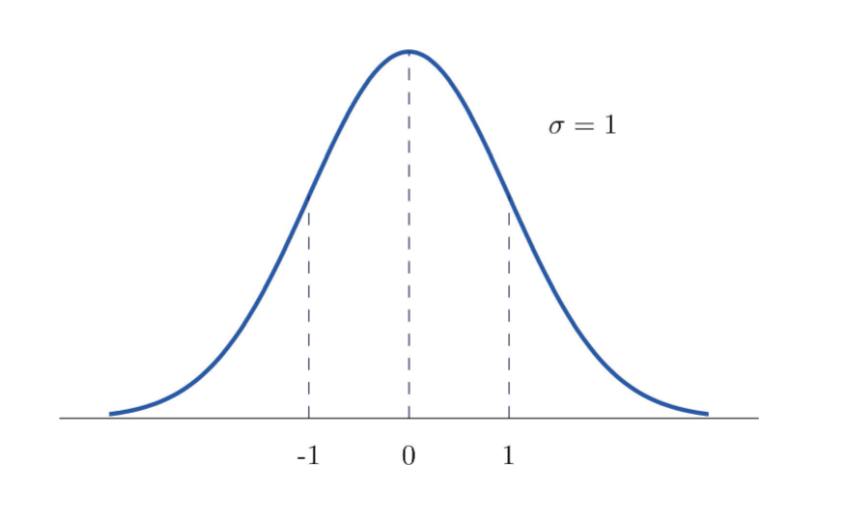
  • the standard normal is one set of parameters for a normal distribution

    • example of curves with different means and standard deviations

    • 

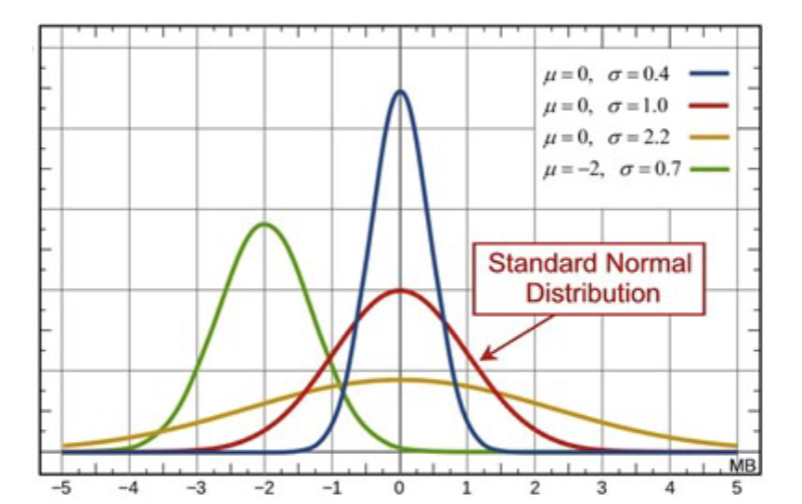
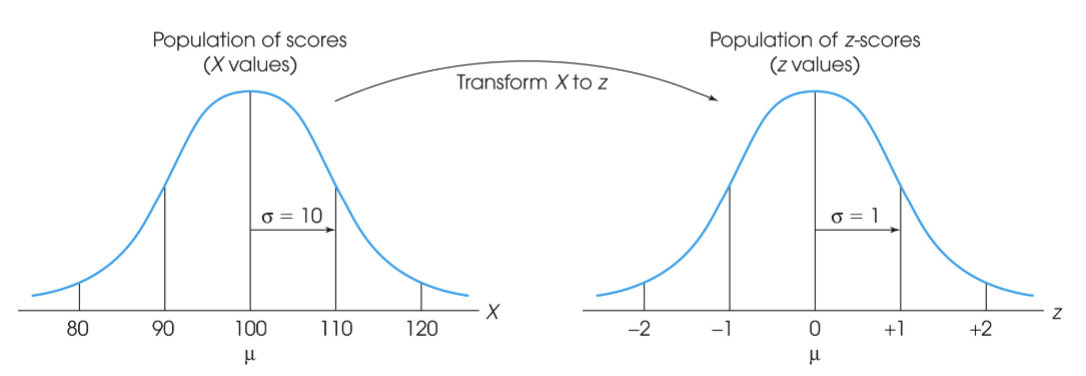
  • any normal distribution can be standardized to a standard normal distribution which is defined as having a μ=0 and σ=1

    • 

  • a z score expresses a score as a standardized score indicating where it lies on the standard normal curve

    • 

  • z scores refer to scores in terms of distance in standard deviations from the mean and initial units are ignored

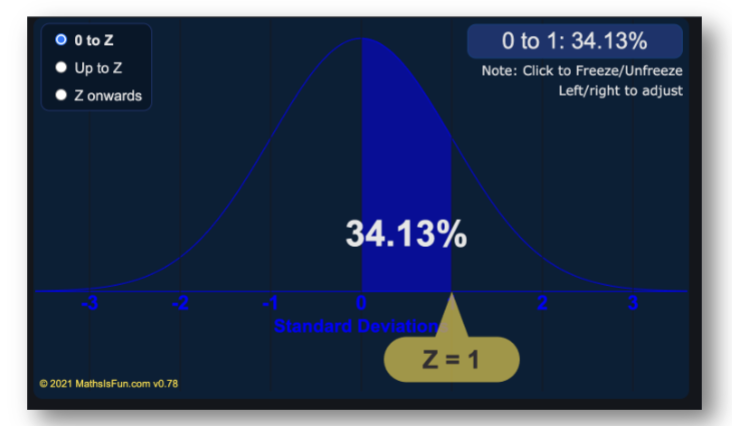
    • a z score of 1 always means 1 standard deviation above the mean

    • 

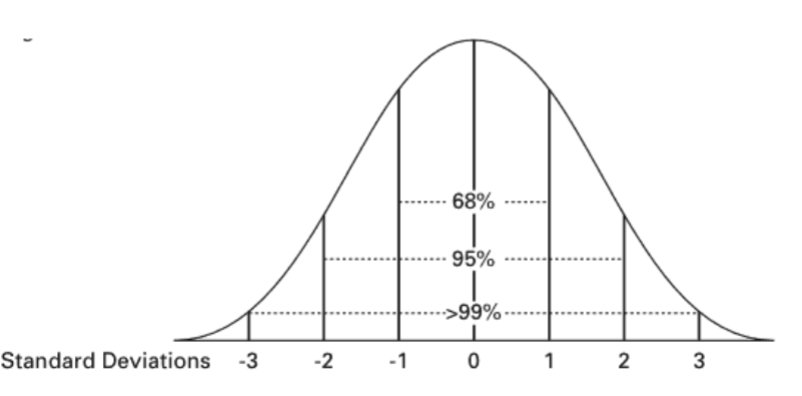
computing z scores

• to compute a z score you need-

  • the score you want to convert to a z score (x_i)

  • the mean of the distribution (x bar)

  • the standard deviation of the distribution (s)

    • 

example with world happiness data

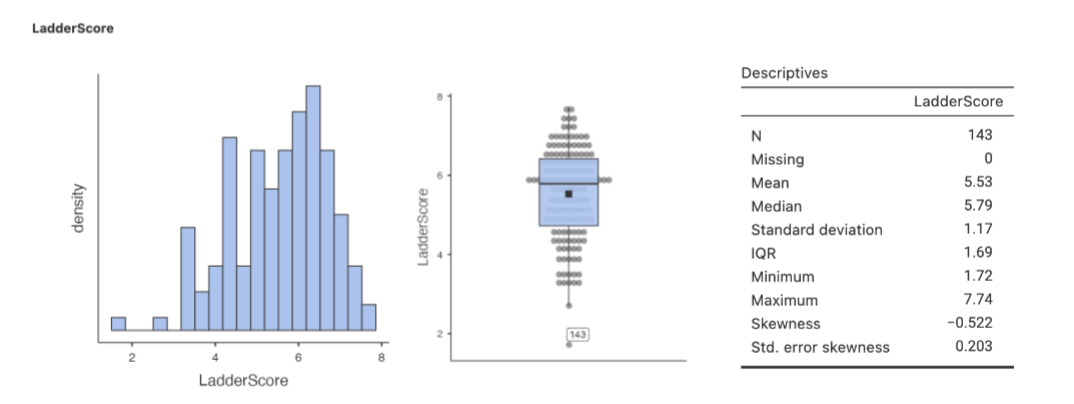
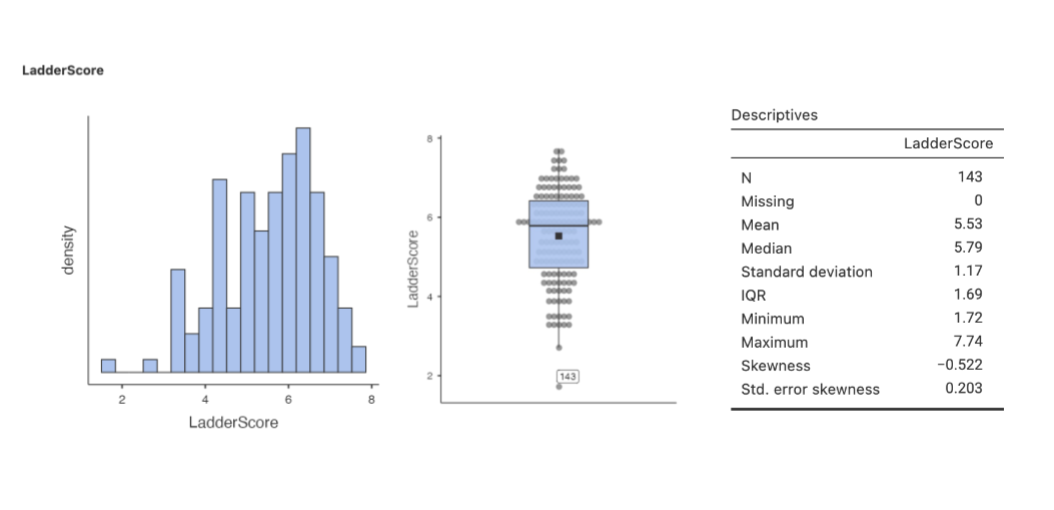
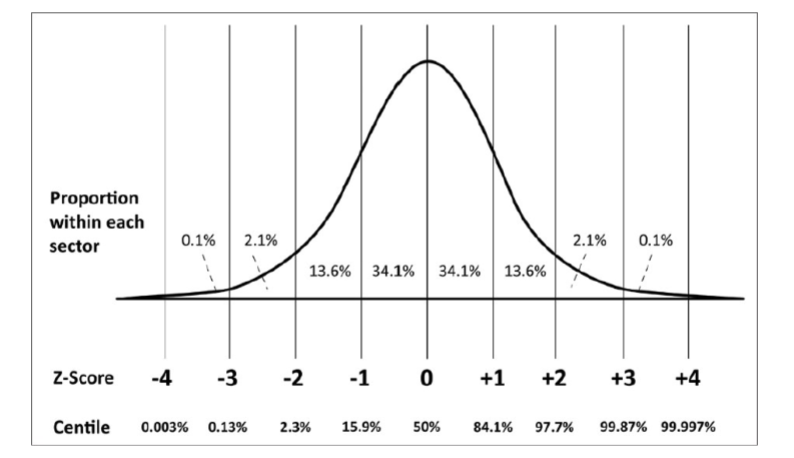
• standard curve gives us easy access to information about proportion under the curve

  • 

  • 

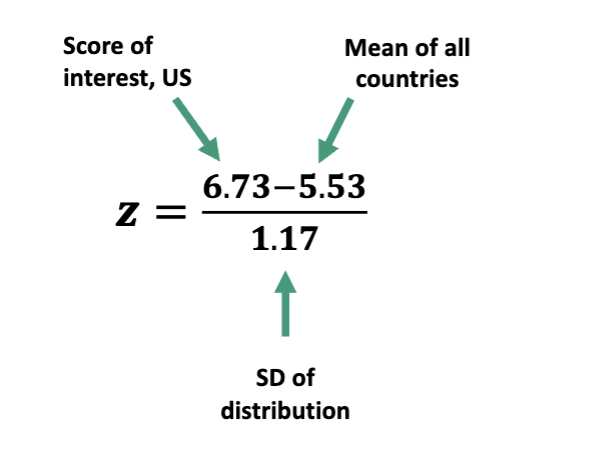
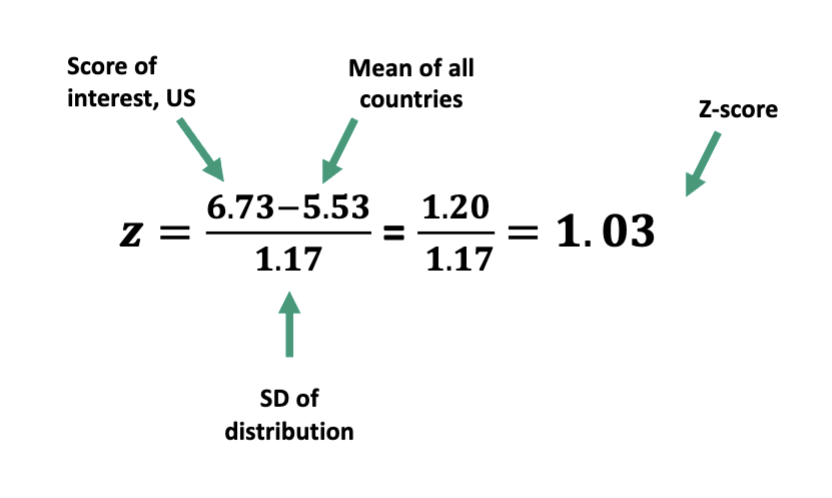
to calculate a z score for a given raw score

• divide by the standard deviation, then add the mean

• divide by the standard deviation, then subtract the mean

• subtract the mean, then divide by the standard deviation

• subtract the mean, then divide by the variance

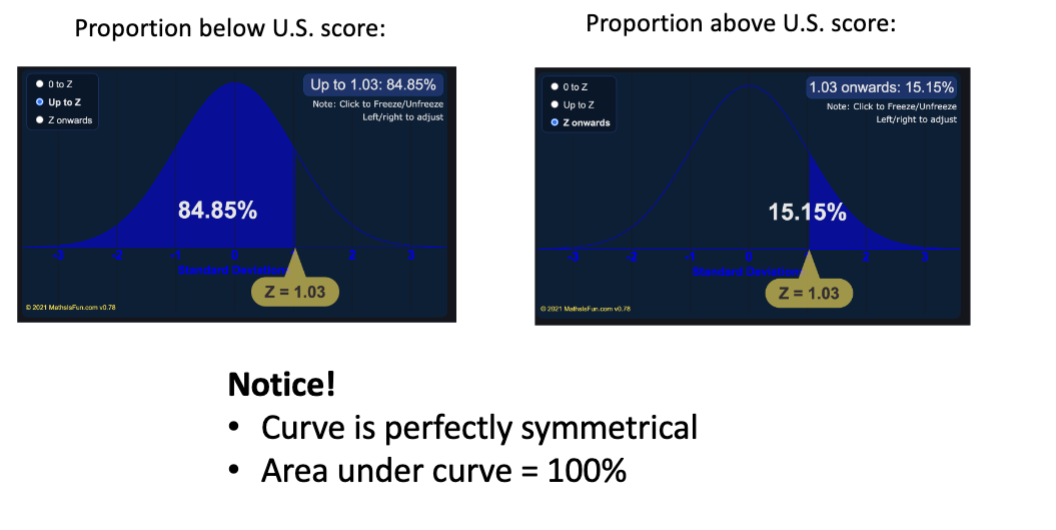
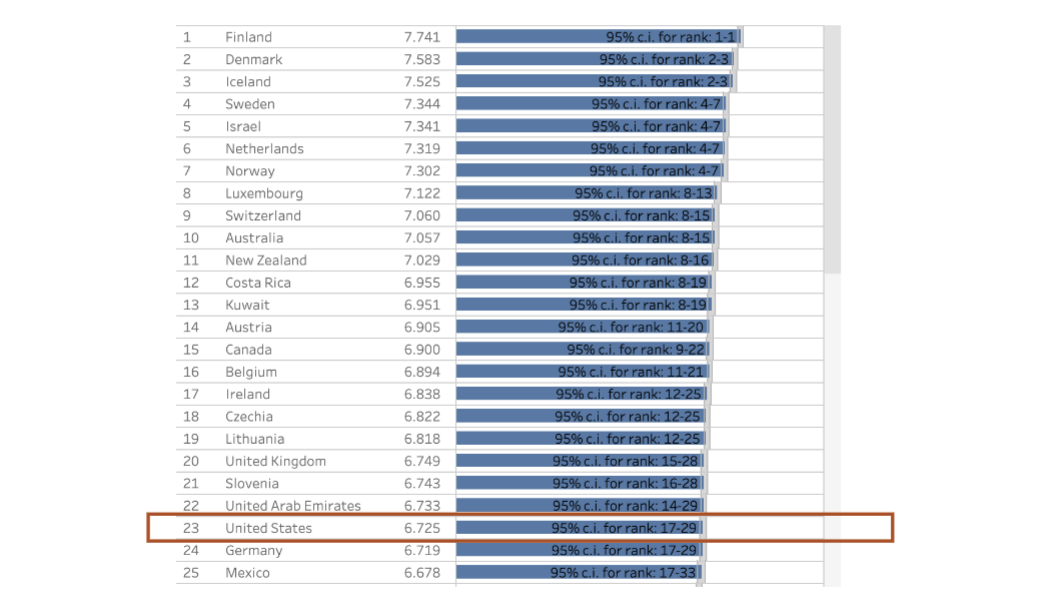
example application with Gallup Poll

• in 2012 the United States had an average self-reported happiness of 7.27

  • did we become less happy relative to other countries?

• how can we compare our happiness relative to the world for the latest report (score of 6.73) to our score about 10 years ago in 2012 (score of 7.27)?

  • Z SCORE!!!!

z scores give you a tool to make comparable scores for variables that are on different scales of measurement

z scores can help identify highly unusual scores that are “outliers”

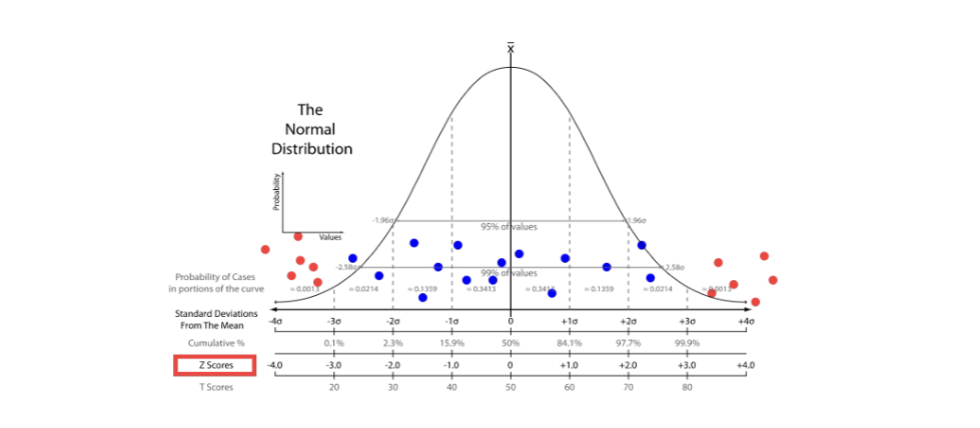
a common benchmark is to consider all scores less than or greater than 3 standard deviations from the mean as outliers

z scores in your stats toolbox

1. compare relative standing of scores from different distributions (from different points in time)

2. create comparable scores for variables that are measured in

   different units so they can be compared directly or used to

   compute an average “composite score” (different kinds of homework scores likes quizzes and tests)

3. use benchmark of standard deviation to determine whether a

   score is an outlier (scores less than or greater than 3

   standard deviations were considered outliers, what is an

   alternative benchmark for variability to do this? HINT: how

   Jamovi labels outliers in box plots)