AP Physics C Mechanics Unit 1: Kinematics

1.1 Scalars and Vectors

Scalars and Vectors

• vectors: have size and direction

  • magnitude and direction

  • component form: r = ai + bj + ck

    • i = y

    • j = x

  • use pythagorean theorem to find length

  • length is absolute value

  • find angle by taking inverse tangent

• scalars: do direction, only size

Vector Addition:

• tip to tail vector addition (geometric)

  • pointed end is tip

  • other end is tail

  • place tip of one vector to tail of other vector it is being added/subtracted

• subtraction is same

  • A - B = A + (-B)

Analytical Vector Addition

• R = Resultant = A + B

• R_x = A_x = B_x

• R_y = A_y + B_y

• To find the magnitude and direction of the resultant vector, we can use the following equations:

  • |R| = √(Rx² + Ry²)

  • θ = tan⁻¹(Ry / Rx)

Multiplying Vectors

• when vector A is multiplied by scalar c

  • magnitude of vector becomes absolute value of cA

  • if c is positive, direction of vector does not change

  • if c is negative, direction is reversed

• same rules for division

Vector form in two dimensions:

• General form:

  • U + V = (U_x + V_x)j + (U_y + V_y)i

• Ex: V = 225m at 50º west of north, U = 130m at 32º south of west

  • if measure from x axis, 50º west of north becomes 140, 32º south of west becomes 212

    • V_x = V cos (140) = 225 cos (140) = -172 m

    • V_y = V sin (140) = 225sin (140) = 145 m

    • U_x = U cos 212 = 130 cos 212 = -110 m

    • U_y = U sin 212 = 130 sin 212 = -69 m

    • V = -172i + 145j

    • U = -110i - 69j

    • V + U = -282i + 76j

    • use pythagorean theorem with values from V + U and find size

    • use inverse tangent to find angle

One dimensional extending to three dimensions

• Three dimensional:

  • U + V = (U_x + V_x)j + (U_y + V_y)i + (U_z + V_z)k

1.2 Displacement, Velocity, Acceleration

Position

• defined as the location of an object in space relative to a chosen reference point

• often represented as a vector quantity that includes both magnitude and direction.

displacement: change in postion

• if object moves relative to reference frame, then the object’s position changes

  • displacement is change in position

• x_f-x_i = displacement

  • change in x

• represented by x with arrow

• vector quantity

• convert to meters

Distance

• magnitude or size of displacement between two positions

• distance travelled = TOTAL length of path travelled between two positions\

• scalar quantity

Time

• change or the interval over which change occurs

• impossible to know time passed without change

• elapsed time = change in time/ dt / t_f-t₀

average velocity

• change in x / change in t = v_avg

• dt/dx = v_avg

• area under curve gives displacement (change in x)

  • use definite integral

• V_avg = (v_i + v_f)/2

  • for constant acceleration only

• vector quantity

instantaneous velocity and acceleration

• a_avg = (change in v) / (change in t)

  • dv/dt

• slope of secant line gives average velocity

• slope of tangent line gives instantaneous velocity

• area under slope

• the greater the acceleration, the greater the change in velocity over given time

• average acceleration is rate at which velocity changes

• acceleration when velocity either changes magnitude or direction or both

• vector quantity

  • same direction as change in velocity

• when object slows, acceleration is opposite to direction of motion

  • deceleration

• instantaneous acceleration is at specific instant in time

  • da/dt

Speed

• scalar quantity

• instantaneous speed is magnitude of instantaneous velocity

• average speed is distance travelled divided by elapsed time

  • d/dt

1.3 Representing Motion

Position v Time Graph

• x axis is time

• y axis is postion

• velocity = slope

  • create velocity v time graph with velocity value

    • y axis is velocity, x axis is position

  • slope = acceleration

    • create acceleration v time graph with acceleration value

      • y axis is acceleration, x axis is position

• if acceleration = 0, velocity is constant

• slope at any point ins instantaneous velocity at that point

  • found by finding slope of tangent line

    • derivative

• Velocity v displacement graph

  • velocity is x axis, displacement is x axis

• V² v displacement graph is linear

  • y = mx + b

    • v² = (slope) (change in x) + v₀²

      • (v² - v₀²)/ change in x = slope

Kinematics: Properties of Motion

• V = V₀ + at

  • only applicable with constant acceleration

    • same as for other mechanics equations

• displacement is area of velocity v time graph

  • area = integral of graph

    • it is approximately triangle, so use that formula for area:

      • displacement = ½ vt

      • displacement = ½ at²

• a = v/t

• v = at

• displacement = ∫ vt (dt) on [t₀,t]

• change in velocity = ∫ at (dt) on [t₀,t]

1 Dimensional Kinematics Problem Solving Steps

1. Examine situation to determine which physical principles are involved

   1. draw sketch

2. make a list of what is given or can be assumed from the problem as stated

   1. identify knowns and unknowns

3. find an equation or set of equations to help solve the problem

   1. use list of knowns and unknowns

4. substitute knowns along with units into appropriate equation and obtain numerical solutions complete with units

5. check to see if answer is reasonable

Gravity

• if air resistance and friction are negligible, all objects fall towards center of earth with same constant acceleration, independent of mass

  • feather and brick same speed

• air resistance opposes motion of object through air

• friction between objects also opposes motion between them

• no air resistance or friction = free fall

• acceleration constant with no air resistance of friction

• g = 9.8m/s² = acceleration

1.4 Reference Frames and Relative Motion

• V_{(object moving)(point of view)} = Velocity of object with respect to perspective being observed

• V_HE = V_HM + V_ME

  • first subscript on both sides of equation should be the same

  • last subscript on both sides of equation should be the same

  • middle subscripts cancel out

  • V_HM = -V_MH

Relative Velocity

• velocity of object is relative to medium - sum of velocity vectors

  • medium has velocity relative to an observer

Relative Velocities and Classical Relativity

• Relativity: study of how different observers moving relative to each other measure the same phenomenon

  • classical relativity is limited to situations where speeds are less than about 7% of the speed of light

1.5 Motion in 2 or 3 Dimensions

Motion in 2D

• vertical velocity does not impact horizontal velocity and vice versa

  • horizontal motion is independent of vertical motion

  • vertical motion is independent of horizontal motion

• projectile motion is special case of 2D motion that has zero acceleration in one dimension and constant nonzero acceleration in second dimension

  • unless explicitly mentioned, modeled without including effects of air resistance

• represented with three vectors

  • one shows the straight line path between the initial and final points of the motion

  • one shows the horizontal component of the motion

  • one shows the vertical component of the motion

    • add horizontal and vertical components to give straight line path

      • solve with pythagorean theorem

        • remaining vector is hypotenuse

• specify direction of vector relative to some reference frame using arrow having length proportional to vector’s magnitude and pointing in direction of vector

Projectile Motion

• motion of an object thrown or projected into the air, subject only to the acceleration of gravity

• object is projectile, path is trajectory

• motions alone perpendicular axes are independent and can be analyzed separately

• s is total displacement

  • components are x and y

• range is horizontal distance R traveled by a projectile

  • the greater the initial speed, the greater the range

• neglecting air resistance, maximum range is Θ = 45º

  • without neglecting, maximum range is Θ = 38º

• When launching a projectile, the initial angle of projection plays a crucial role in determining its range; thus, adjusting the angle below or above 45º will result in a shorter range.

• if R is larger, earth curves below projectile and acceleration of gravity changes

  • object will go into orbit

• R = (v₀² sin2Θ₀)/g

Steps to Analyze Projectile Motion

1. Resolve or break the motion into horizontal and vertical components alone the x and y axes

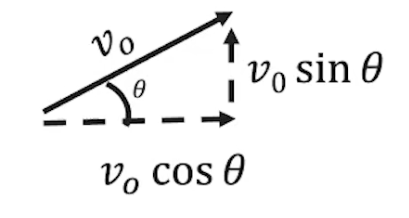
   1. A_x = AcosΘ A_y = A sinΘ

   2. V_x = VcosΘ V_y = VsinΘ

      1. v is only magnitude of velocity

2. treat the motion as two independent 1D motions

   1. applying the kinematic equations to each direction to solve for displacement, velocity, and acceleration

   2. x = x₀ + v_xt

   3. v_x = v_x0 = velocity is a constant

   4. a_y = -9.8 m/s²

   5. y = y₀ + 1/2(v_0y + v_y) t

   6. v_y = v_0y - gt

   7. v²y = v_0y² - 2g(change in y)

3. Solve for unknowns in two separate motions

4. recombine two motions to find total displacement

Motion in 2D at Angle

• the higher the launch angle the higher the initial velocity

  • initial velocity and launch angle have direct relationship

• launched at higher than 45º, less distance covered and less speed horizontally

  • more distance vertically

• launched at less than 45º, more distance covered and greater speed horizontally

  • less distance vertically

• optimal launch angle for maximum range is 45º

• use trig functions to mathematically determine velocity

  • sohcahtoa

• sin for vertical velocity

• cos for horizontal velocity

• motions along perpendicular directions are independent

• A_x + A_y = A

• unknown angle is inverse tan (A_y / A_x)

• A_x = Acos(θ) and Ay = Asin(θ), where θ is the angle between the resultant vector A and the horizontal axis