Transformations

The idea of a transformation is taking a graph depiction and stretching, smushing, moving, or transforming the graph in different directions.

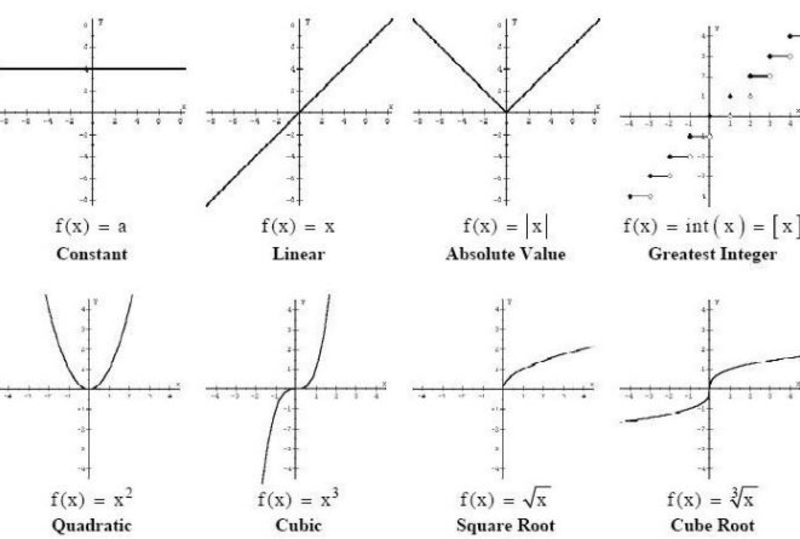
Here are the base graph types used to start transformations:

• Y=X : Linear base graph

• Y=X² : Quadratic base graph

• Y=X³ : Cubic base graph

• Y=IxI : Absolute value base graph

• Y=sqrt(x) : Square root base graph

• Y=³sqrt(x) : Cube root base graph

Transforming Points

To perform transformations, we must identify the key points to work with. For linear, it will most likely be the intercept point. For quadratic, the vertex point, intercepts, and mirror points. For absolute value, the mirror points on either side. (in equations the points are usually provided)

Using Horizontal and Vertical shifts and Dilations, We can move these points around.

• For the point (1,5)

• (1,5) shifted two to the right is (3,5)

• Shifted two to the left is (-1,5)

• Shifted two down (1,3)

• Shifted two up (1,7)

• Stretched horizontal by factor of 2 (2,5)

• Shrunk horizontal by factor of 2 (1/2,5)

• Stretched vertical by factor of 2 (1,10)

• Shrunk vertical by factor of 2, (1,5/2)

• Use these steps for all points individually.

Horizontal Translation/Shift

This occurs when we move a graph to the right or left. The function for this movement is:

• f(x-k) : Shift right by k amount of units

• f(x+k) : Shift left by k amount of units

  For example, if we had y=(x-3)², since f(x) is the same as y=x, we would graph (x-3)² as a parabola (quadratic base graph) and then shift the entire parabola 3 units to the right.

Vertical Translation/Shift

This occurs when we move the graph up or down. Since f(x)=y, the function for this is similar to the y intercept:

• f(x)+k : Shift up by k units

• f(x)-k : Shift down by k units

  For example, if we had y=x²+2, we know we have a quadratic base graph because of the squared variable (parabola). We then take that parabola and move it up two units.

  For another example, if we had y=Ix+1I-2, we have multiple transformations and should work from the inside out. Remember, inside parenthesis=horizontal, outside=vertical. We use the absolute value base graph and move it left by one unit and down by two units.

Vertical Dilation

If we change just the Y or X values instead of moving the entire shape, we are now stretching or shrinking the graph. The function for this is modeled by:

• cf(x) or y=cf(x): Streches the graph by factor of c

• 1/cf(x) or y=1/cf(x): Shrinks the graph by factor of c

  We use these functions by multiplying the y value or f(x) by c or 1/c. An example is y=2sqrt(x). Here we see that two is outside of parethesis therefore effecting y. sqrt(x) leads us to the square root base graph. We then take those graph points and multiply their y values by 2.

Horizontal Dilation

This is done “inside” the equation for parentheses. This function is modeled by:

• y=f(cx): Shrinks the graph by factor of c, when doing this you must divide all inside parenthesis by c

• y=f(1/cx): Stretches the graph by multiplying by c

  For example, y=(2x)². We identify the base graph as parabola or quadratic. Then, we divide the x values of the points by 2 or multiply by 1/2.

Reflecting Graphs

This means taking the graph and mirroring or flipping it, the function for this is modeled by:

• f(-x) if there is a negative sign inside parentheses, you reflect horizontally

• -f(x) if there is a negative sign outside parentheses, you reflect vertically

This can be achieved by making all the Y or X values negative

Symmetry

There are Odd and Even transformation graphs

• Even graphs look like the mirror image of each other on both sides of the y axis

• Odd graphs look the same, except one side will also be reflected over the x axis

• if f(-x)=f(x) it is even

• if f(-x)=-f(x) then it is odd

• if (0,0) is not a point it will not be odd

SUMMARY

This equation summarizes transformations, lets break it down

af(bx-c)+d

• a=vertical dilation

• b=horizontal dilation

• c=horizontal shift

• d=vertical shift