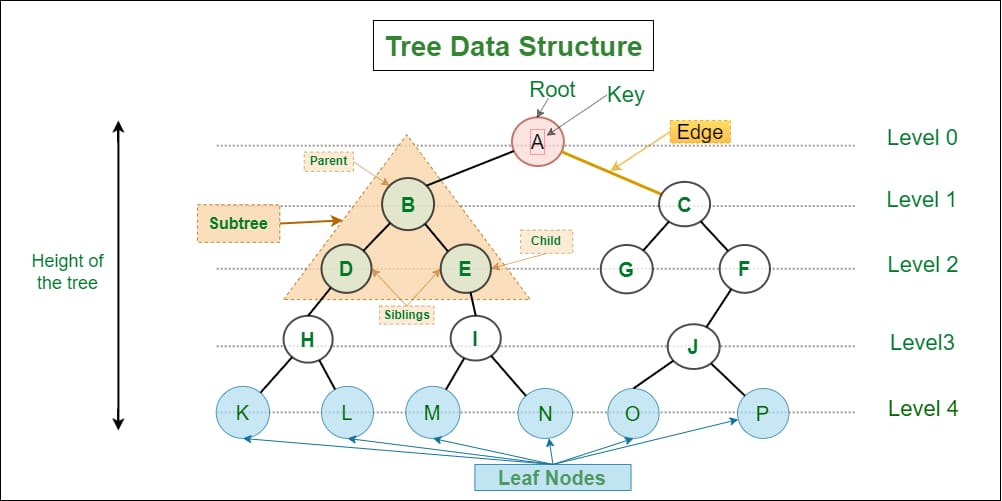
TREE TERMINOLOGY
Certainly! Here’s a comprehensive list of tree terminology commonly used in data structures:
### Basic Terms
1. Node: The fundamental part of a tree that contains data and may have links to other nodes.
if we have N number of nodes then we can have a maximum of N-1 number of links also called as Edges.
2. Root: The topmost node of a tree. It has no parent.
3. Leaf: A node with no children; it is at the end of a branch.
4. Edge: The link between two nodes.
5. Parent: A node that has one or more child nodes.
6. Child: A node that is a descendant of another node (its parent).
7. Subtree: A tree formed by a node and its descendants.
### Types of Trees
1. Binary Tree: A tree in which each node has at most two children (left and right).
2. Binary Search Tree (BST): A binary tree where each node’s left children are less than the node, and each node’s right children are greater.
3. Balanced Tree: A binary tree where the height difference between the left and right subtrees of any node is minimal.
4. Complete Binary Tree: A binary tree in which all levels are fully filled except possibly the last, and all nodes are as far left as possible.
5. Full Binary Tree: A binary tree in which every node has either 0 or 2 children.
6. Perfect Binary Tree: A binary tree where all internal nodes have exactly two children and all leaf nodes are at the same level.
7. AVL Tree: A self-balancing binary search tree where the difference between heights of left and right subtrees cannot be more than one.
8. Red-Black Tree: A balanced binary search tree with additional properties to ensure balance.
### Tree Properties
1. Height: The length of the longest path from the root to a leaf node.
2. Depth: The length of the path from the root to a specific node.
3. Level: The level of a node is the number of edges from the root to the node. The root is at level 0.
4. Degree: The number of children a node has.
5. Depth of Tree: The maximum depth among all nodes in the tree.
6. Height of Tree: The height of the root node or the maximum level among all nodes in the tree.
### Traversal Methods
1. Pre-order Traversal: Visit the root node, then recursively visit the left subtree, followed by the right subtree.
2. In-order Traversal: Recursively visit the left subtree, visit the root node, then recursively visit the right subtree.
3. Post-order Traversal: Recursively visit the left subtree, the right subtree, and then visit the root node.
4. Level-order Traversal: Visit nodes level by level from the root to the leaves.
### Specialized Trees
1. Trie: A tree-like data structure used to store a dynamic set of strings, where nodes represent prefixes of the strings.
2. B-Tree: A self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time.
3. Segment Tree: A binary tree used for storing intervals or segments, allowing querying of segment overlaps efficiently.
### Binary Tree Properties
1. In-order Successor: The node that comes immediately after a given node in in-order traversal.
2. In-order Predecessor: The node that comes immediately before a given node in in-order traversal.
### Miscellaneous Terms
1. Sibling: Nodes that share the same parent.
2. Ancestor: A node’s parent, grandparent, and so on up to the root.
3. Descendant: A node’s children, grandchildren, and so on down to the leaves.
4. Subtree: A tree consisting of a node and its descendants.
5. Path: A sequence of nodes and edges connecting a node with a descendant.
### Tree Example
For a binary tree:
```
1
/ \
2 3
/ \ / \
4 5 6 7
```
- Root: 1
- Leaves: 4, 5, 6, 7
- Parent of 2: 1
- Children of 2: 4 and 5
- Depth of node 3: 1
- Height of tree: 2 (longest path from root to leaf)
This terminology covers the fundamental aspects of trees used in computer science and programming. Understanding these terms helps in grasping various tree-based algorithms and data structures.
Tree is a non sequential, non linear and hierarchical data structure. Using trees we can store data in a hierarchical manner.
Tree data structure simulates the hierarchical relationship between the data elements, for example files and directories.
In tree data structure, every individual element is called as Node. Node in a tree data structure, stores the actual data of that particular element and link to next element in hierarchical structure.
if we have N number of nodes then we can have a maximum of N-1 number of links also called as Edges.
A tree data structure can be defined recursively as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references (edges) to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.
A tree can also be defined as a collection of 'N' nodes out of which one designated as root node and 'N-1' edges such these 'N-1' edges follows from the fact that each edge connects some node to its parent and every node expect the root has one parent and also any child can have only one parent.
A generic tree diagram would look like this:
Important points about trees
Every linear list is trivially a tree, because single linked list of N nodes has N-1 links
A tree contains no cycles.
Every node has a parent except for the root node
Every child node has only one parent. No child has two parents.
A tree can not have more than one root node.
Root Node
In a tree data structure the first node is known as the Root Node. Root node is the only node in the tree that does not have a parent. Every tree mush have a root node. Root node can be visualized as the origin of the tree. There can be only one root node for a tree. A tree cannot have multiple root nodes.
Edge
In a tree data structure the connecting link between any two nodes is called as an Edge. Every edge defines a parent-child relationship between the nodes. The node nearer to the root is the parent and the other is the child.
Parent
In a tree data structure a node which is a predecessor of any node is called as the Parent of that node. A node which has at least one children is called as Parent Node
Child
In a tree data structure a node which is a descendent of any node is called as the Child of that node. A node that has a parent is called as the child node. In a tree data structure a parent node can have any number of child nodes. In a tree all nodes are child nodes except for the root node.
Siblings
In a tree data structure, nodes with same parent are called as the Sibling nodes.
Leaf Node
In a tree data structure a node with no children is called as the Leaf Node. Leaf node is also known as "External Nodes" or "Terminal Nodes".
Internal Node
In a tree data structure a node that has atleast one child is called as Internal Node. Internal Nodes are also known as "Non - Terminal Nodes".
Degree
In a tree data structure, the degree of a node is defined as the total number of children for that node. The highest degree of a node among all the nodes in a tree is called as "Degree of Tree"
Level
In a tree data structure the root node is said to be in Level 0 all the the children of root are said to be in Level 1 and so on. In other words, for all the nodes in level N , their children will be present in the level N+1.
Height
In a tree data structure, the height of a node is defined as the total number of edges present in the longest path from that node to any leaf node of the tree. Height of the root node is considered as the height of the tree. The height of all the leaf nodes is 0. Among all the nodes root has the highest height.
Depth
In a tree data structure, the depth of a node is defined as the total number of edges present in the longest path from that node to the root node of the tree. For any tree the depth of the root node is 0. The highest depth of the node among all the nodes is called as the depth of the tree.
Path
In a tree data structure, the sequence of nodes and edges from one node to another node is called as the Path between the two nodes. The length of the path is number of edges in the path.