Note on Interest Rates and Cash Flow Analysis

Page 4: Finding the Rate

• Determining Interest Rates

  • Necessary for evaluating future cash flows.

  • Important for:

    • Return on investment.

    • Interest rate on loans.

• Single Cash Flow/Perpetuity Evaluation

  • Rearranging PV or FV equations to solve for r:

    • Formula: ( r = \left( \frac{FV_n}{PV} \right)^{\frac{1}{n}} - 1 )

• Cash Flow Streams (Annuities)

  • Use Excel or financial calculators for precise values.

  • Trial and error for rough estimations.

Page 5: Example Problem

• Investment Scenario

  • Invested: $863.75 today.

  • Future Value: $1,000 in 5 years.

• Calculation

  • Rearranged formula: ( 863.75 = \frac{1000}{(1 + r)^5} )

  • Result: Rate of return is 2.97%.

Page 6: Finding the Number of Periods (n)

• Rearranging Equations

  • Formula: ( n = \frac{\ln(FV/PV)}{\ln(1 + r)} )

• Example Problem

  • Car purchase: $20,000 needed.

  • Current investment: $15,000 at 10% per year.

  • Calculate time to reach $20,000.

Page 7: Finding Cash Flow - Loan Example

• Loan Structure

  • Principal: Amount borrowed.

  • Repayments include principal and interest.

  • Amortization table used to track payments.

• Principal Owing

  • Present value of loan repayment cash flows.

Page 8: Loan Problem

• Car Purchase Loan

  • Amount: $10,000 for 5 years at 5% interest.

• Questions to Consider

  1. Annual payment amount.

  2. Principal paid in year 4.

  3. Interest paid in year 4.

  4. Amortization table creation.

Page 9: Loan Solutions

1. Annual Payment Calculation

   • Formula: ( PV = C \left( \frac{1 - (1 + r)^{-N}}{r} \right) )

   • Result: Annual payment is $2,309.75.

2. Principal Paid in Year 4

   • Calculation: Principal paid = $2,095.01.

3. Interest Payment in Year 4

   • Interest = $214.74.

4. Amortization Table

   • Detailed breakdown of payments over 5 years.

Page 12: Summary So Far

• Understanding PV and FV Calculations

• Rearranging Formulas for Missing Variables

• Considerations for Real-Life Applications

  • Loan/mortgage payment frequencies.

  • Interest rate quotations.

Page 13: Future Value and Compounding

• Compounding Mechanics

  • Interest earned on principal and previously earned interest.

• Simple vs. Compound Interest

  • Simple interest: Interest on principal only.

  • Compound interest: Includes interest on interest.

Page 14: Example Problem - Compound Interest

• Investment Scenario

  • $100 at 10% for 5 years.

• Calculations

  • Compound FV: $161.05.

  • Simple Interest: $50.

  • Interest on interest: $11.05.

Page 16: Simple Interest for Less Than a Year

• Calculation Method

  • Discount factor:

    

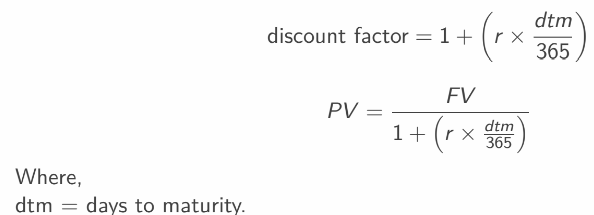
Page 17: Compounding Frequency Impact

• Continuous Compounding

  • Formula: ( FV_{\infty} = PV \times e^{r \times n} ).

Page 21: Different Types of Rates

1. Annual Percentage Rate (APR)

   • Simple interest earned in one year.

2. Effective Annual Rate (EAR)

   • Total interest earned including compounding.

3. Equivalent n-Periodic Rate (r)

   • Discount rate for adjusting cash flows.

Page 22: APR Details

• APR Characteristics

  • Nominal interest rate, does not account for compounding.

  • Required disclosure on loans and savings.

Page 24: Effective Annual Rate (EAR)

• Conversion from APR

  • Formula: ( 1 + EAR = \left(1 + \frac{APR}{m}\right)^m ).

Page 26: Compounding Effect

• Comparison of Compounding Intervals

  • Higher frequency leads to higher EAR.

Page 28: EAR to Periodic Discount Rate

• Conversion for Non-Annual Cash Flows

  • Formula: ( r_{per period} = (1 + EAR)^{\frac{1}{n}} - 1 ).

Page 32: APR to Discount Rate

• Conversion Steps

  1. Convert APR to EAR.

  2. Convert EAR to r for cash flow frequency.

Page 36: Nominal vs. Real Interest Rate

• Definitions

  • Nominal: Before inflation.

  • Real: Adjusted for inflation.

• Fisher Equation: ( 1 + r_{nominal} = (1 + r_{inflation})(1 + r_{real})