Chapter 9: Momentum

9.1 Momentum

• The momentum p of a particle is the product of its mass m and velocity v:

  

  • Unit: kg⋅m/s

• Momentum is a vector quantity; it has the same direction as the particle’s velocity and can be represented by components.

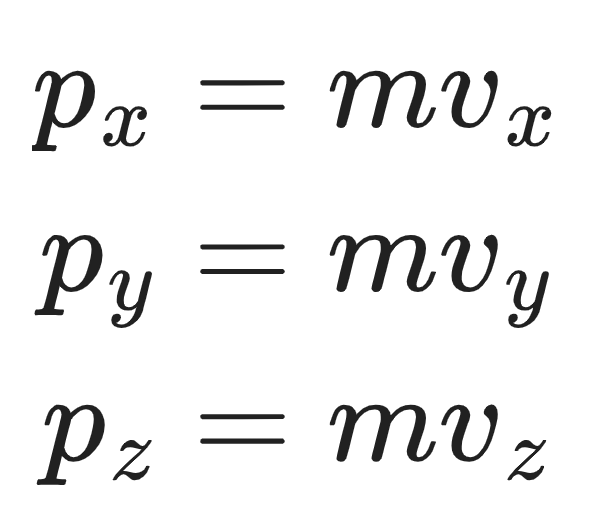
• When m is constant, we can express Newton’s second law for a particle in terms of momentum.

• Thus, Newton’s Second Law can be restated as follows:

The vector sum of forces acting on a particle equals the rate of change of momentum of the particle with respect to time.

• Mathematically,

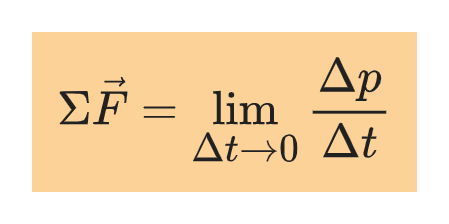
• The total momentum P of any number of particles is equal to the vector sum of the momenta of the individual particles:

  

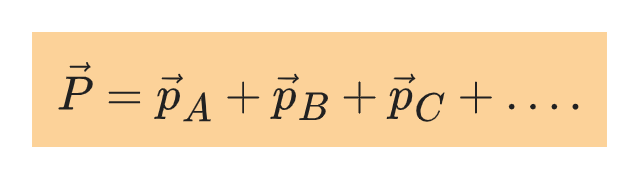
Example 9.1 Preliminary Analysis of a Collision

A small compact car with a mass of 1000 kg is traveling north on Morewood Avenue with a speed of 15m/s. At the intersection of Morewood and Fifth Avenues, it collides with a truck with a mass of 2000 kg that is traveling east on Fifth Avenue at 10m.s. Treating each vehicle as a particle, find the total momentum (magnitude and direction) just before the collision.

Solution

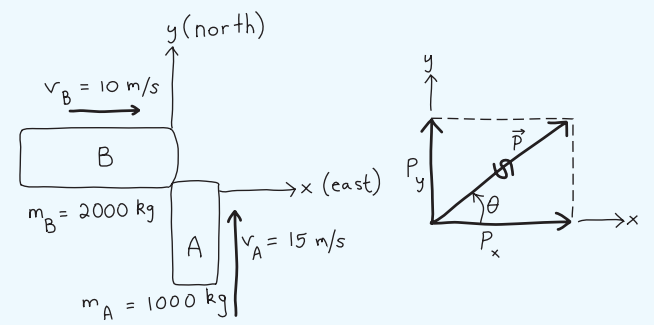
• Let object A be the small compact car and object B be the truck.

• We can find the components of the total momentum using the definition of total momentum (in component form), therefore:

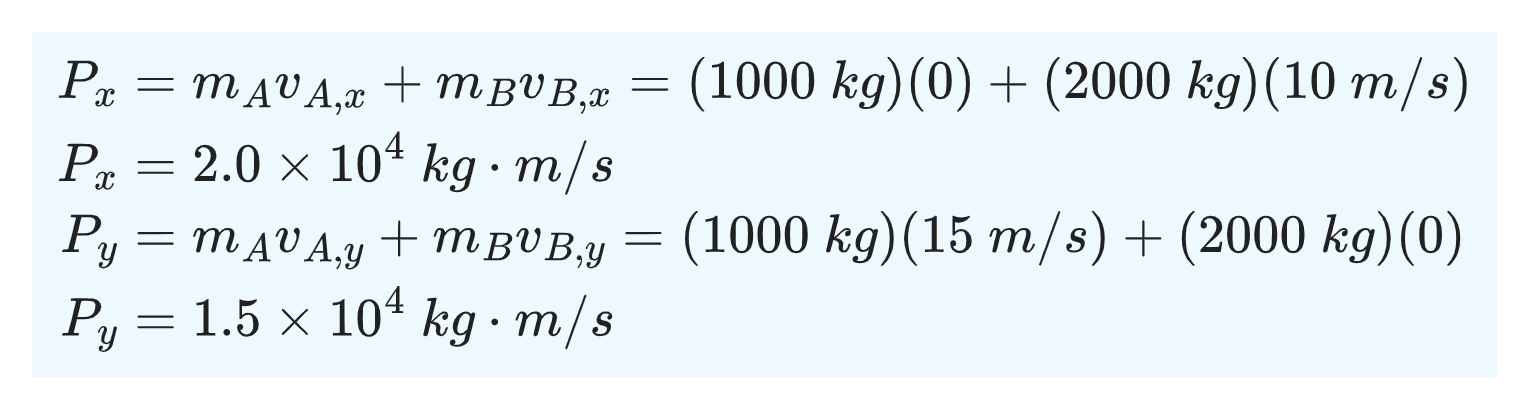
• We can now calculate the magnitude and direction of the total momentum before the collision using the x- and y-components.

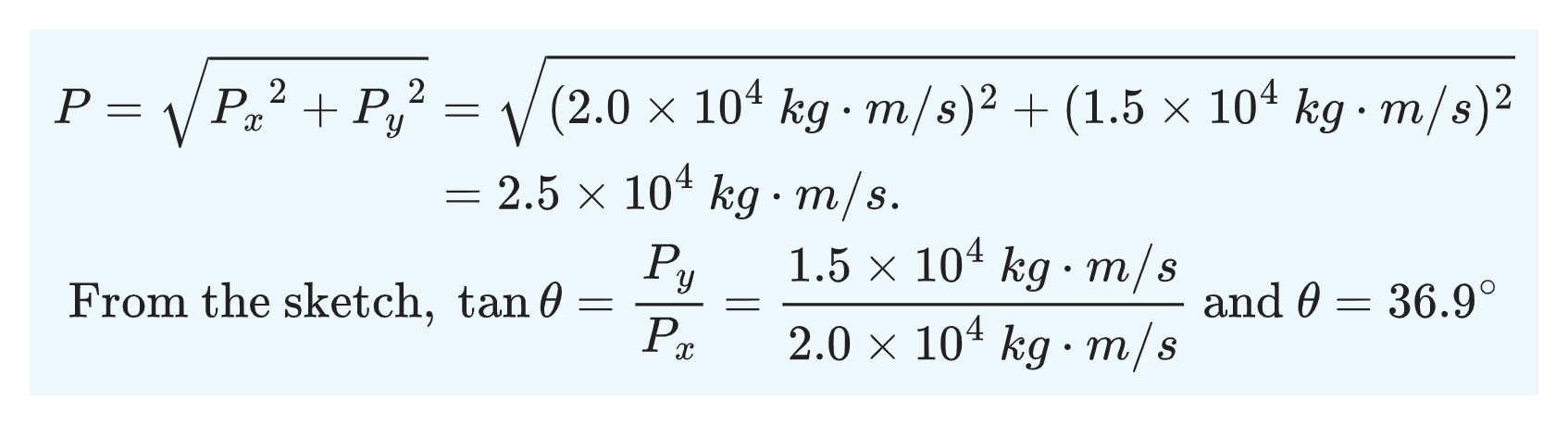
9.2 Conservation of Momentum

• The total momentum of a system is constant when the net external force on the system is zero.

  • A system is a definite collection of particles and a system acted upon by no external forces is referred to as an isolated system.

  • This principle is a direct consequence of Newton’s third law.

• The principle of conservation of momentum can sometimes be used when external forces act on the system.

  • If the internal forces (forces exerted by particles or objects within the system) are much larger than the net external force acting on the system, we may use an idealized model that neglects the external forces during the actual collision.

Example 9.2 Astronaut Rescue

An astronaut finds herself floating in space 100 m from her ship when her safety cable becomes unlatched. She and the ship are motionless relative to each other. The astronaut’s mass (including space suit) is 100 kg; she has a 1.0 kg wrench and only a 20-minute air supply. Thinking back to her physics classes, she devises a plan to use conservation of momentum to get back to the ship safely by throwing the wrench away from her. What is the magnitude of her recoil velocity if she throws the wrench at 10m/s? Will her recoil velocity be enough to get her back to the spacecraft before she runs out of air?

Solution

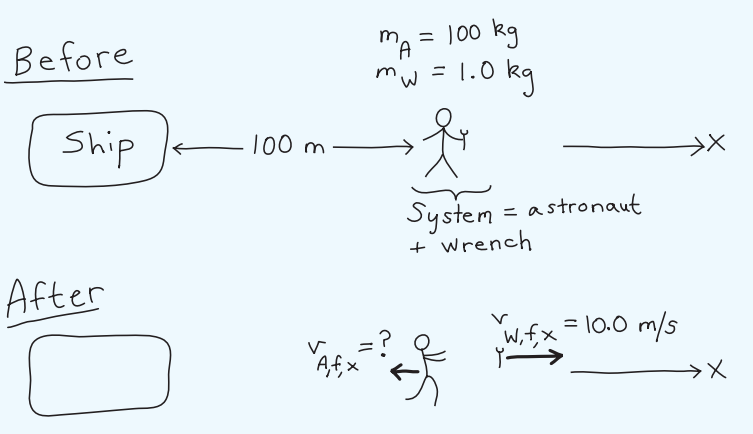
• Let A be the astronaut and W be the wrench. Let +x be the direction in which she throws the wrench.

• Here, the system is the astronaut and the wrench. Applying conservation of momentum we have,

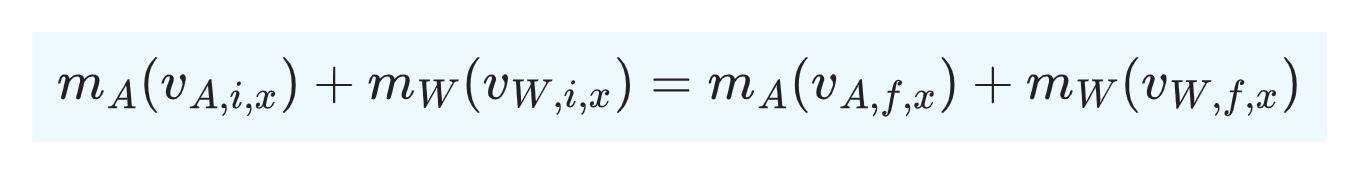
• The initial velocity of each object is 0, so L.H.S=0. And, we have:

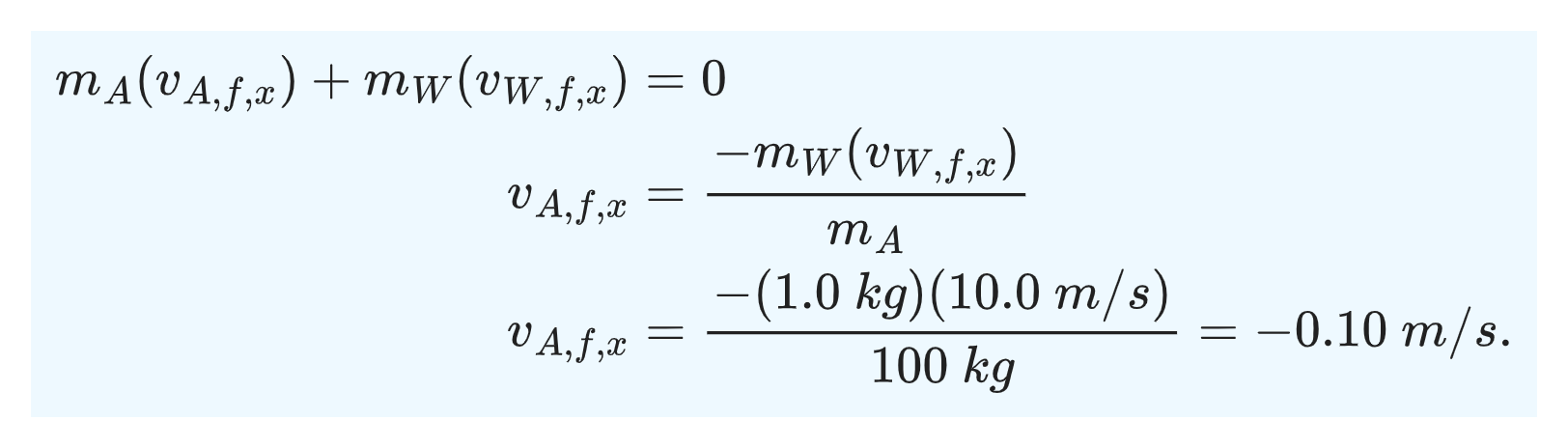
• Using x=vt, we find the time it takes her to get back to the spacecraft

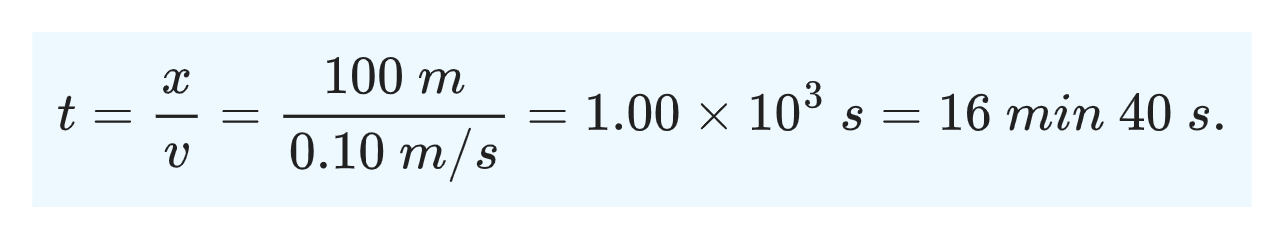
• Therefore, her recoil velocity is enough to get her back to the spacecraft before she runs out of air.

9.3 Inelastic Collisions

• Any strong interaction between two objects that lasts a relatively short time is called a collision.

• In any collision in which external forces can be ignored, momentum is conserved: The total momentum of the colliding objects has the same value just after the collision as just before the collision.

  

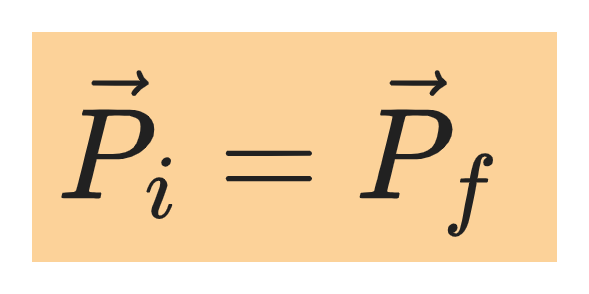
• In an inelastic collision between two bodies, the final kinetic energy is less than the initial kinetic energy. If the two bodies have the same final velocity, the collision is completely inelastic.

• A bit of algebra gives the ratio of final to initial kinetic energy of a completely inelastic collision as:

  

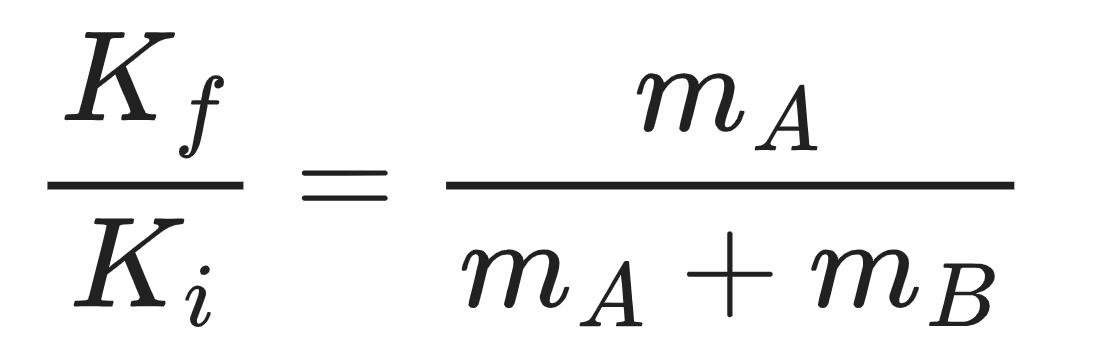
  • As expected, the right side of this equation is always less than 1 indicating that final kinetic energy of the system is less than the initial kinetic energy.

Example 9.3 Inelastic collision on air track

Two (Velcro®-equipped) gliders move toward each other on a linear air track, which we assume is frictionless. Glider A has a mass of 0.50 kg and glider B has a mass of 0.30 kg; both move with initial speeds of 2.0 m/s. Find the final velocity of the joined gliders and compare the initial and final kinetic energies.

Solution

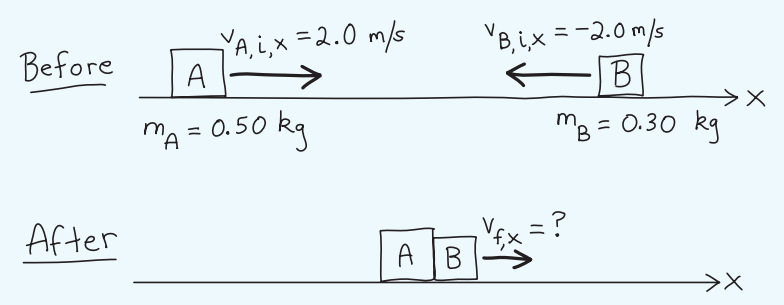
• Since the air track is assumed frictionless, there is no horizontal external force on the system of the two gliders and the x component of momentum is conserved. Let +x be to the right, so

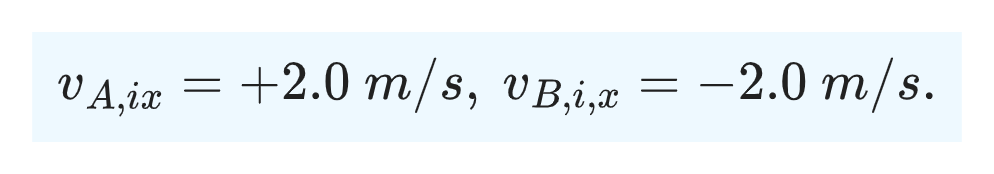
• From the conservation of the x component of momentum, we have

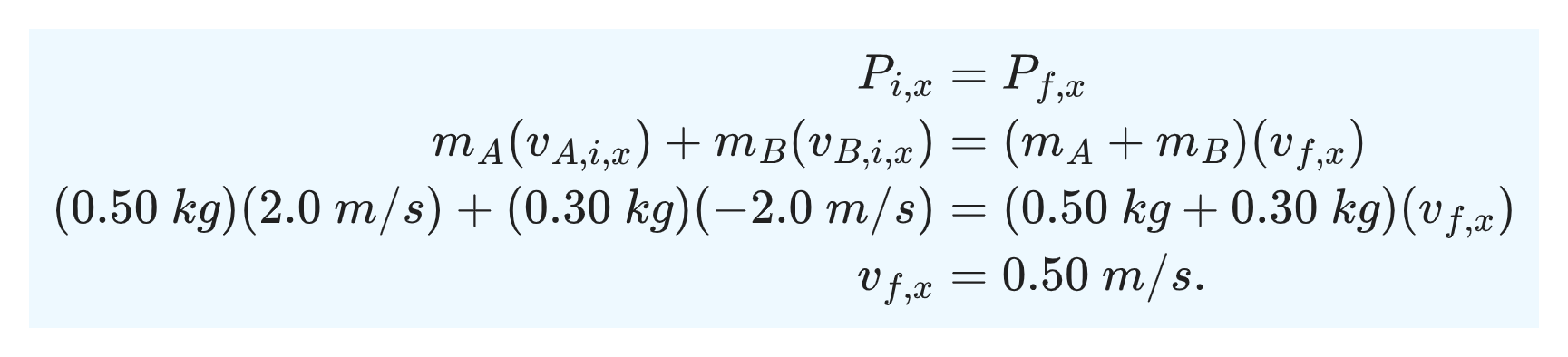
• For each object, K=1⁄2 mv².

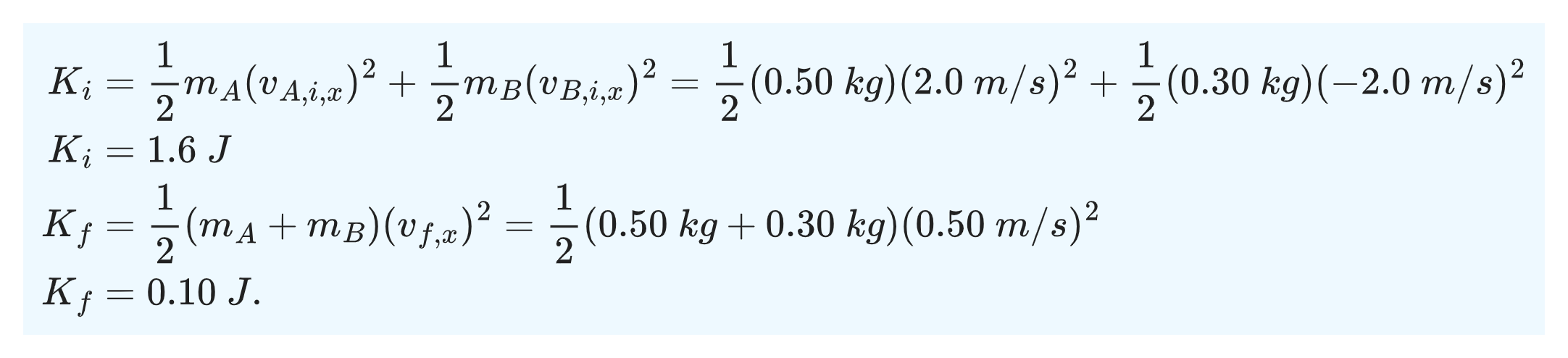
• The final kinetic energy is less than the initial.

9.4 Elastic Collisions

• In an elastic collision between two bodies, the initial and final kinetic energies are equal, and the initial and final relative velocities have equal magnitudes but opposite directions.

  • 

Example 9.4 Elastic collision on air track

Two pucks collide on a frictionless air-hockey table. The pucks have equal masses m = 0.20 kg. Puck A has an initial velocity of 4.0 m/s in the positive x direction and a final velocity of 2.0 m/s at an angle of 60° to the +x axis. Puck B is initially at rest. Find the final velocity of puck B (magnitude and direction). Is the collision elastic?

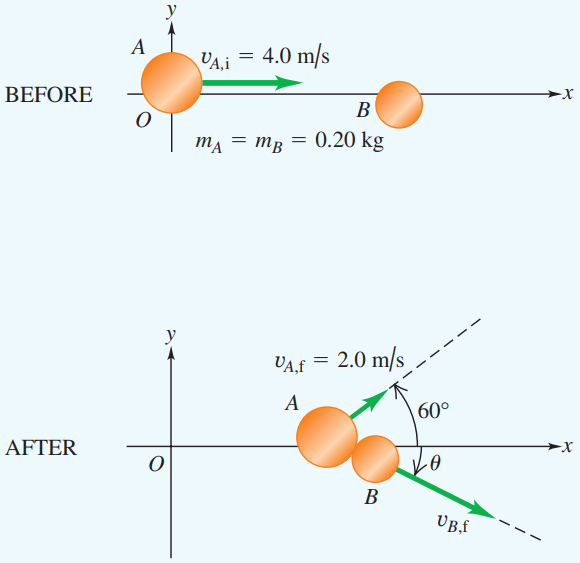
Solution

• Here, the system is the two pucks, the problem involves a two-dimensional collision and so, we write separate conservation equations for the x-component and y-component of total momentum.

• Conservation of the x component of total momentum gives

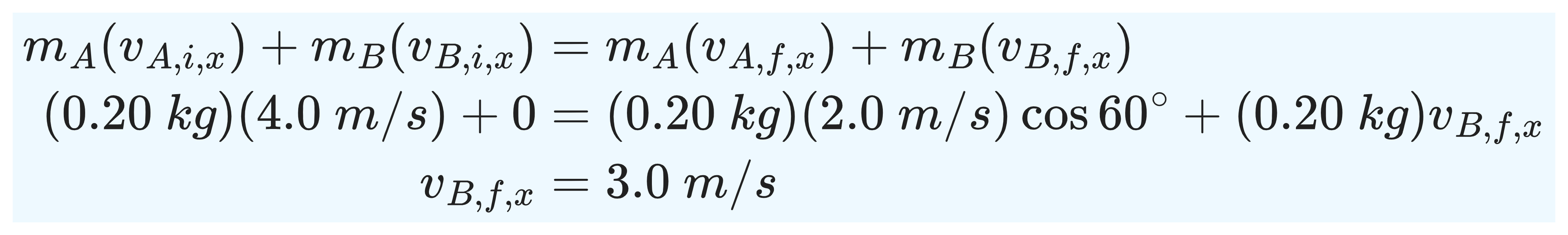
• Conservation of the y component of total momentum gives

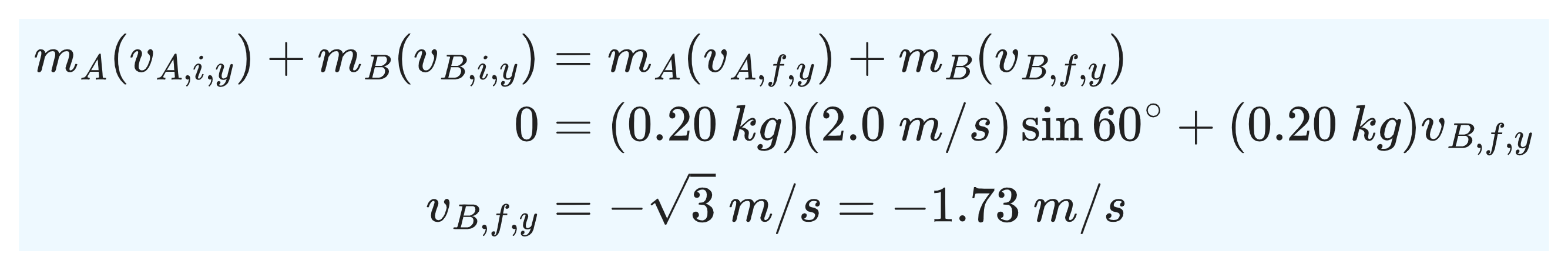
• We can now calculate the magnitude and direction of the final velocity of puck B using the x- and y-components.

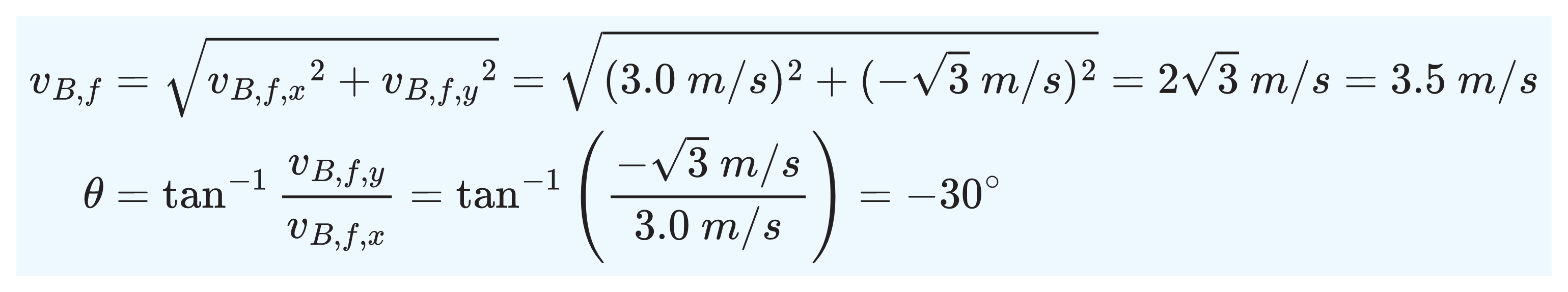
• To determine whether the collision is elastic, we calculate the kinetic energies before and after the collision and then compare.

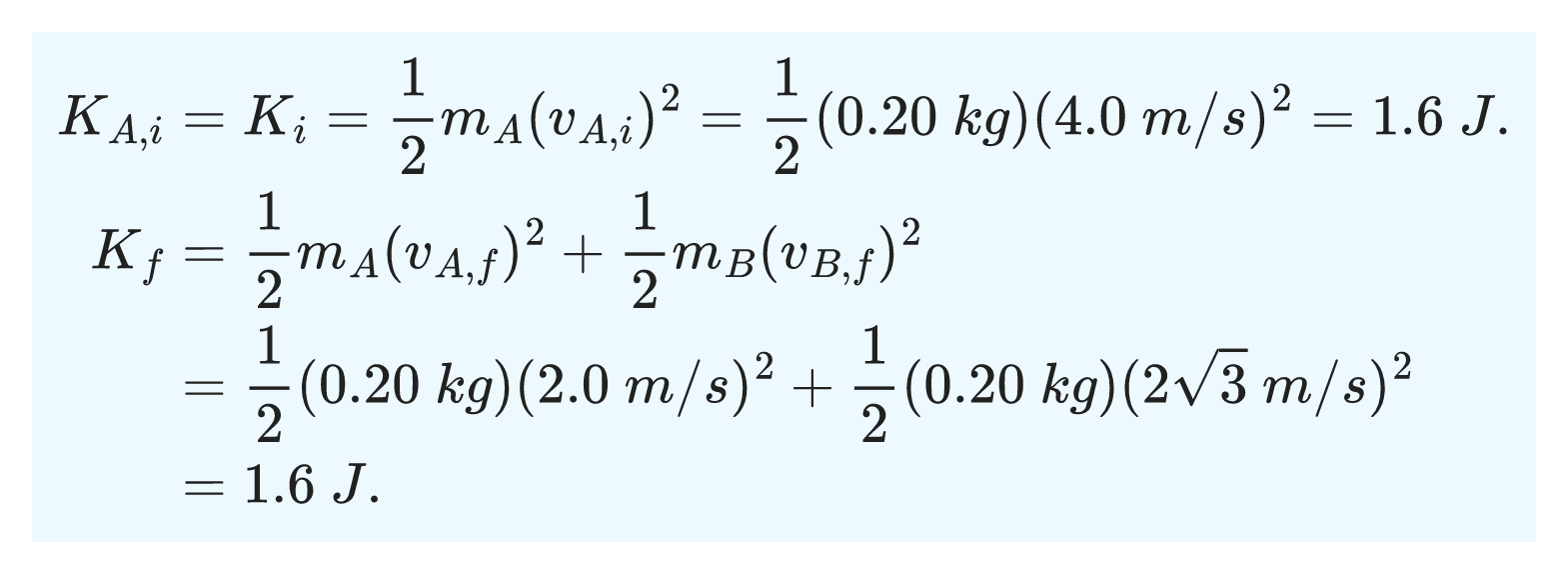
• The total initial kinetic energy is equal to the total final kinetic energy, so the collision is elastic.

9.5 Impulse

• The impulse J of a constant force is the product of force and the time interval over which the force acts:

  

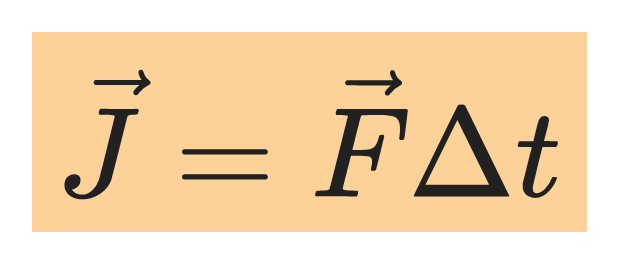
  • Unit: N⋅s

• When the force is not constant, we can define an average force such that the impulse is given by:

  

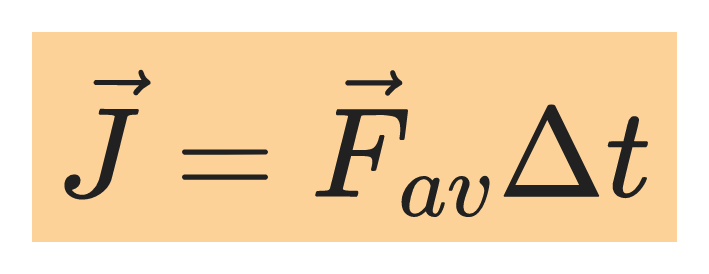
Impulse-Momentum Theorem

• The change in momentum of a particle during any time interval equals the impulse of the total force acting on the particle:

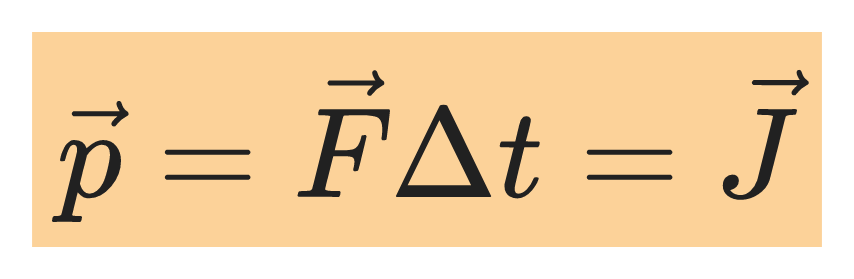
Example 9.5 Kicking a soccer ball

Let’s consider the soccer ball in the figure below. The ball has mass 0.40 kg. Initially it moves horizontally to the left at 20 m/s but then it is kicked and given a velocity with magnitude 30 m/s and direction 45° upward and to the right. Find the impulse of the force and the average force on the ball, assuming a collision time Δt = 0.010 s.

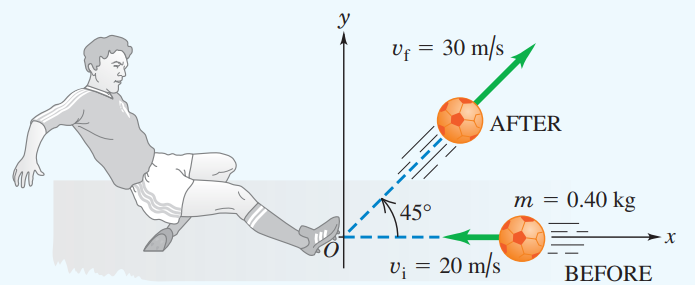
Solution

• Let +x be to the right. Let +y be vertically upward.

• The impulse, and the average force are related by:

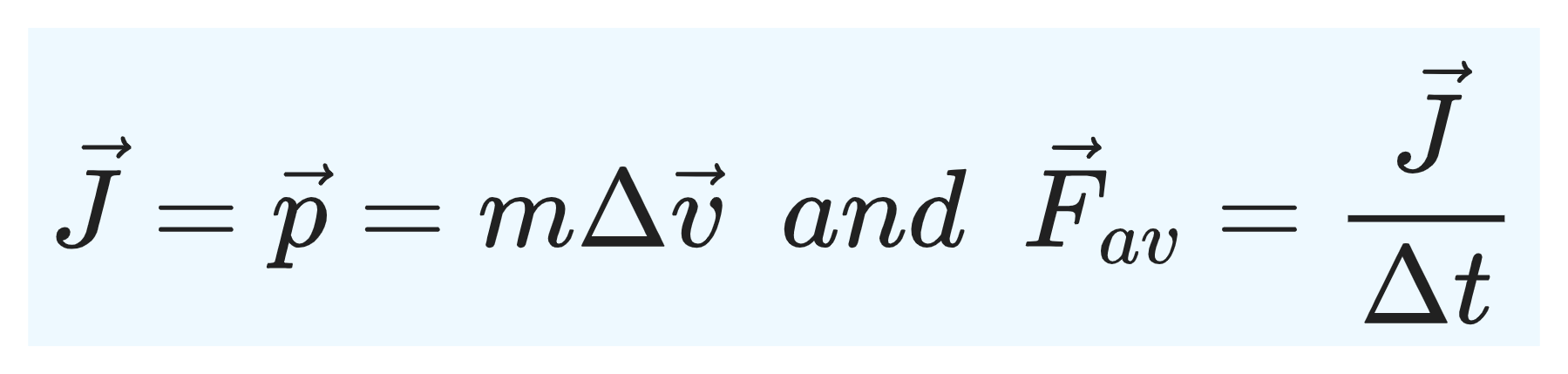
• Applying the equations in component form gives

• The magnitude and direction of the average force are

  

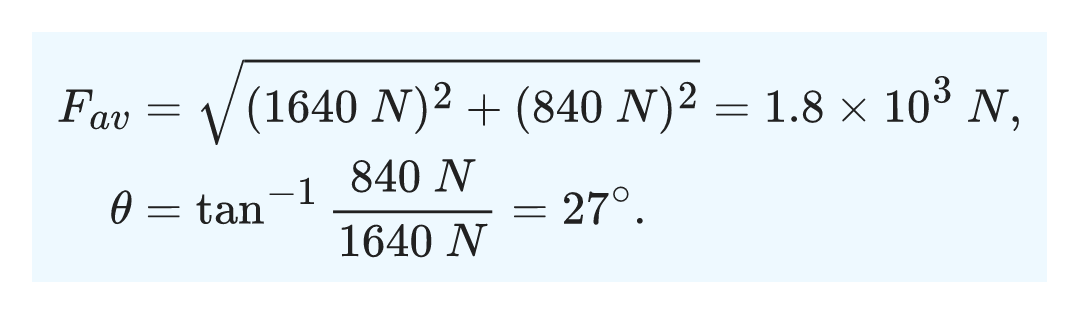
9.6 Center of Mass

• The center of mass of a system of particles is defined as the point having coordinates given by:

  

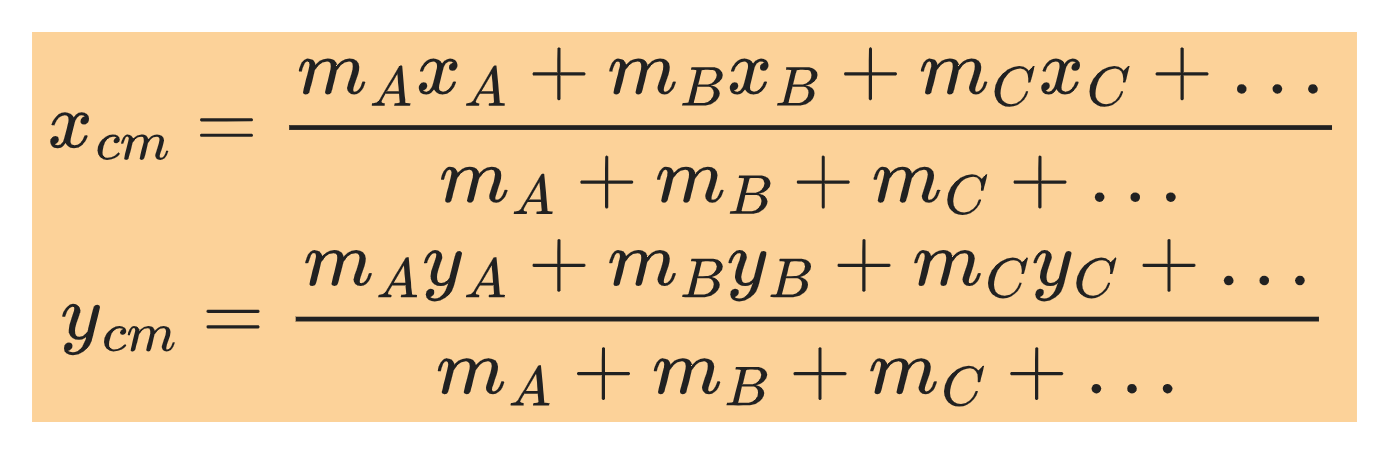
  • where:

    • x꜀ₘ is the x-coordinate of the center of mass.

    • y꜀ₘ is the y-coordinate of the center of mass.

    • A, B, C, … are particles each with mass mᵢ.

• The center of mass of a system is said to be a mass-weighted average position of the particles in the system.

• For a homogenous object with a geometric center, the center of mass is located at the geometric center.

  • Also, if an object has an axis of symmetry, the center of mass lies along it, which may not be within the object.

• When the particles in a system move, the center of mass may also move with a velocity given by:

  

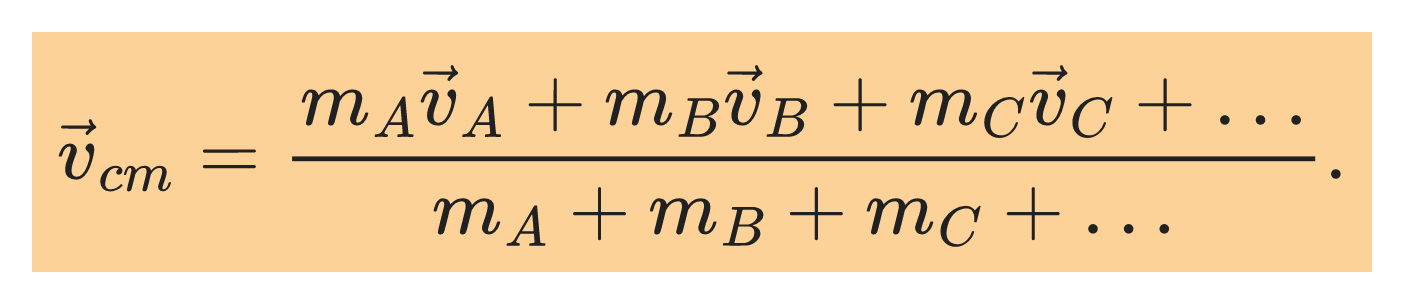
  • where:

    • A, B, C, … are particles each with velocity vᵢ and mass mᵢ.

Total momentum in terms of center of mass

• For a system of particles, the total momentum is given by:

  

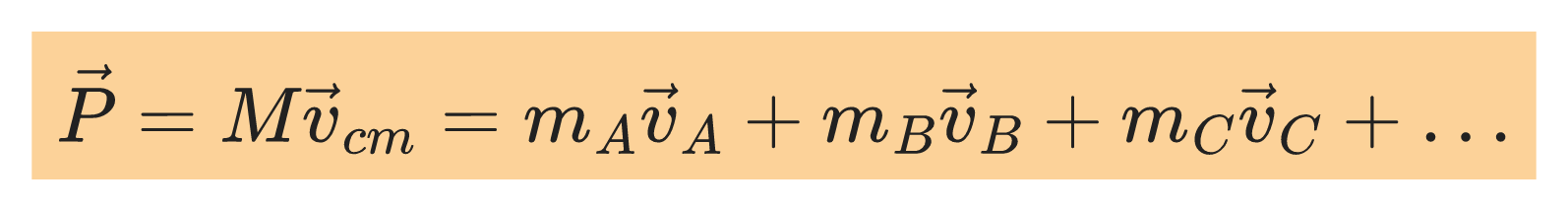
  • where:

    • 

    • v꜀ₘ is the velocity of the center of mass.

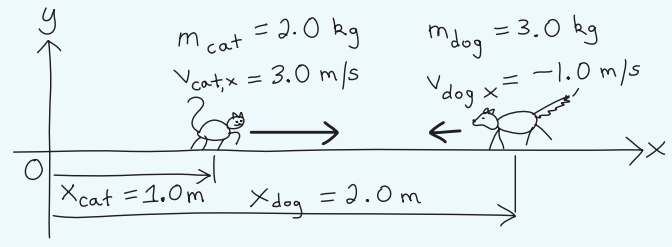
Example 9.6 Quarreling pets

A 2.0 kg cat and a 3.0 kg dog are moving toward each other along the x axis, heading for a fight. At a particular instant, the cat is 1.0 m to the right of the origin and is moving in the +x direction with speed 3.0 m/s, and the dog is 2.0 m to the right of the origin, moving in the -x direction with speed 1.0 m/s. Find the position and velocity of the center of mass of the two-pet system, and also find the total momentum of the system.

Solution

• Applying the equation for position center of mass to the two-pet system:

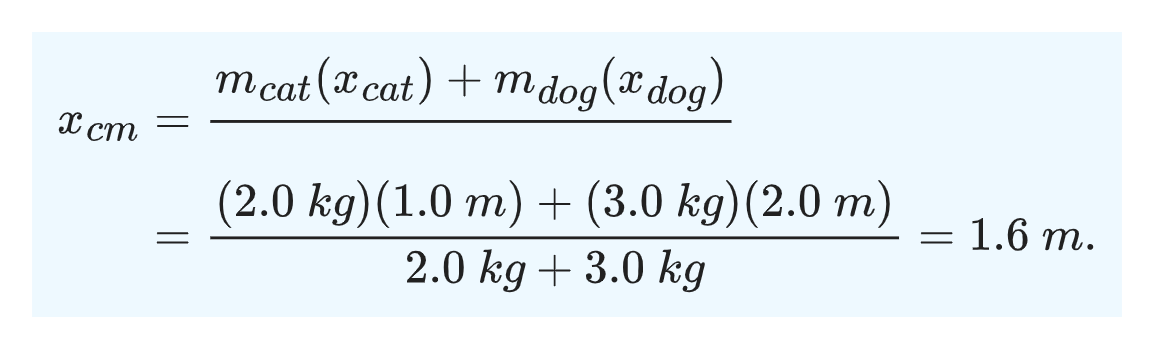
• The velocity of the center of mass of the two-pet system is given by

• The total momentum of the system is the product of the total mass M and the velocity of the center of mass, so we have:

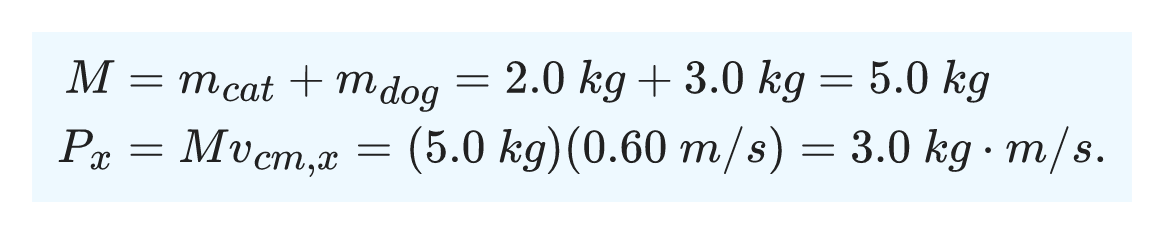
9.7 Motion of the Center of Mass

• When an object or a system is acted on by external forces, the center of mass moves as if all the mass were concentrated at that point:

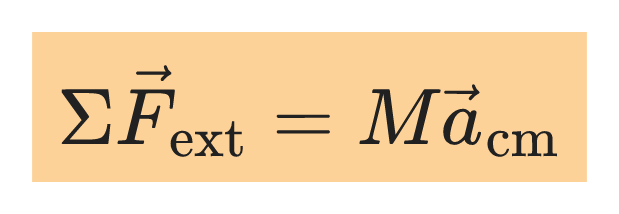
• If the sum of the external forces on a system is zero, the velocity v꜀ₘ of the center of mass is constant, and the total momentum P is also constant.

9.8 Rocket Propulsion

• In rocket propulsion, the mass of the rocket changes as the fuel is burned. Analysis of the momentum relations of the rocket motion must include the momentum carried away by the spent fuel and the momentum of the rocket itself.