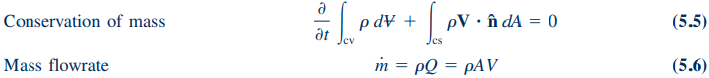NUCL350 Exam 2 Review (Chapters 4 & 5)

Chapter 4 - Fluid Kinematics

Key concepts highlighted by Bindra:

• Eulerian and Lagrangian methods

• velocity fields

• acceleration fields

• Reynolds transport theorem

Chapter Summary and Study Guide from textbook:

Definitions:

• Field representation: Describes how a physical quantity, such as velocity or pressure, varies over space and time.

• Velocity field: A vector field that shows the velocity of a fluid at every point in space and time.

• Eulerian method: Observes fluid flow at fixed points in space as the fluid moves through them.

• Lagrangian method: Tracks individual fluid particles as they move through space and time.

• One-, two-, and three-dimensional flow: Describes fluid flow constrained to one, two, or three spatial dimensions, respectively.

• Steady flow: Flow where fluid properties at any point do not change with time.

• Unsteady flow: Flow where fluid properties vary with time at any point.

• Streamline: A curve that is tangent to the velocity vectors of the flow at every point, showing the direction of the flow.

• Streakline: A line that represents the locus of all fluid particles that have passed through a particular point in space.

• Pathline: The actual path followed by an individual fluid particle over time.

• Acceleration field: A vector field representing the acceleration of fluid particles at every point in space and time.

• Material derivative: The rate of change of a fluid property (such as velocity) as observed from a moving fluid particle.

• Local acceleration: The change in velocity at a fixed point in space over time.

• Convective acceleration: The change in velocity of a fluid particle due to its movement through a velocity gradient in space.

• System: A collection of fluid particles that is observed as it moves through space.

• Control volume: A fixed region in space through which fluid may flow in and out, used for analyzing fluid systems.

• Reynolds transport theorem: A fundamental equation that relates the rate of change of a property in a control volume to the flux of that property across its boundaries.

Equations

Chapter 5 - Finite Control Volume Analysis

Key concepts highlighted by Bindra:

• mass conservation

• linear and angular momentum conservation

• energy conservation

• be able to use Reynolds transport theorem in conservation problems

• be able to do linear momentum balance be able to do control volume problems

• important: be able to get to relative velocity

Chapter Summary and Study Guide from textbook:

Definitions:

• Conservation of mass: The principle that mass cannot be created or destroyed in a closed system.

• Continuity equation: A mathematical expression of conservation of mass in fluid flow, stating that the mass flow rate is constant along a streamline.

• Mass flow rate: The amount of mass passing through a given area per unit time.

• Linear momentum equation: Describes how the momentum of a fluid changes due to forces acting on it.

• Moment-of-momentum equation: Relates the angular momentum of a fluid to the torques acting on it.

• Shaft power: The mechanical power transmitted through a rotating shaft, typically in turbines or engines.

• Shaft torque: The twisting force exerted by a shaft, related to its rotational motion.

• First law of thermodynamics: States that energy cannot be created or destroyed, only transferred or converted from one form to another.

• Heat transfer rate: The amount of thermal energy transferred per unit time.

• Energy equation: Describes the conservation of energy in a fluid system, accounting for internal, kinetic, and potential energies.

• Loss: The dissipation of energy in a system, typically due to friction or inefficiencies.

• Shaft work head: The energy per unit weight of fluid associated with shaft work in a mechanical system.

• Head loss: The reduction in fluid's energy or head due to friction, turbulence, or obstructions in a flow system.

• Kinetic energy coefficient: A factor that accounts for variations in velocity across a flow area when calculating kinetic energy.

Equations: