Newtonian Synthesis

• Until Isaac Newton, it was thought that the ‘physics’ of things outside the Earth – the celestial - was different from that of things on the Earth – the terrestrial.

• Newton rejected this division and applied the same physical laws to both.

  • The force that causes an apple to accelerate as it falls is the same force that holds the Moon to the Earth.

• This unification of the physics governing the celestial and terrestrial is known as Newtonian Synthesis.

• If he had done nothing else in his life, Newton would be world-famous for this contribution alone.

  • Newtonian Synthesis had such a profound effect that one of its consequences was the American Revolution.

• Newton tried to find one ‘Law of Gravity’ to explain the motion of objects here on Earth and the motion of the planets.

• He was aided by 3 facts:

  • He knew the force of gravity upon objects here on Earth. If ‘1’ is the object and ‘2’ is the Earth then the weight of object 1 due to object 2 is

    • F_on1from2=m_1g_2

      • g2 is the acceleration due to the gravity from object 2

  • His 3rd Law tells him that this must also be the force on Earth from the object

    • F_on2from1=m_2g_1

      • where g1 is the acceleration due to the gravity of the object.

  • The motion of the planets around the Sun is described by three laws found sometime earlier by Kepler

Kepler’s Laws

Many decades before Newton, Johannes Kepler discovered three laws of planetary motion based on observation.

The path of each planet about the Sun is an ellipse with the Sun at one focus.

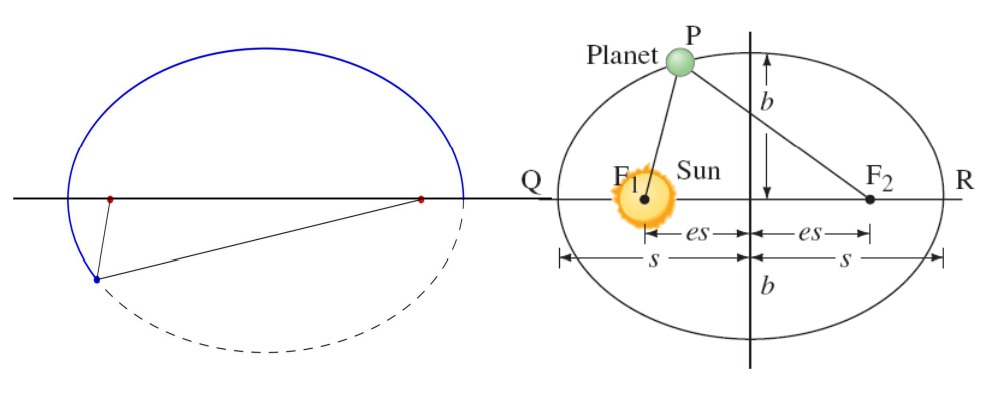
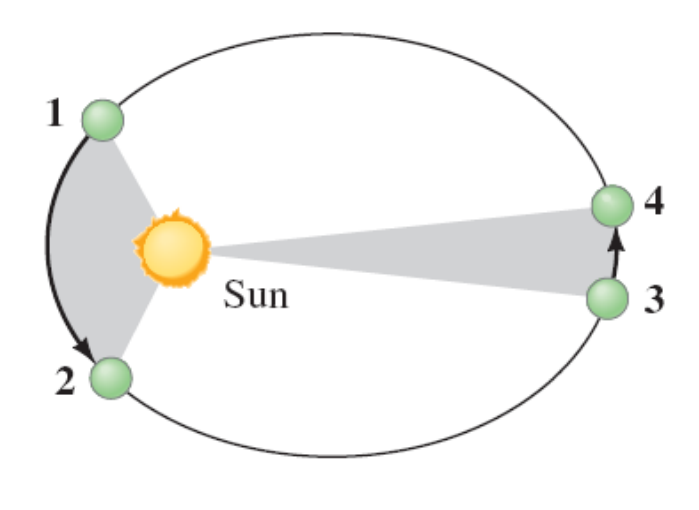
An imaginary line drawn from each planet to the Sun sweeps out equal areas in equal times.

The square of a planet’s orbital period is proportional to the cube of its mean distance from the Sun.

• Since the Sun is at a focus, the mean distance s from the Sun is the same as the semimajor axis.

  • T^2∝s^3

• The ratio of s3 / T2 is the same for all planets.

  • s_1^3 / T_1^2 = s_2^3 / T_2^2

Newton’s Law of Universal Gravitation

• The first two ‘facts’ tell Newton the force of gravity between two objects must be proportional to the product of their masses.

  • g1 must be proportional to m1, g2 must be proportional to m2

• What he doesn’t know is if it depends upon anything else.

• Newton tries an idea that had been suggested by others: the force of gravity decreases as the square of the distance between the two objects.

  • This is called an inverse square law.

• With this assumption and his three Laws of Motion, he is able to derive Kepler’s three laws.

  • Later he shows that any other scaling with distance does not give Kepler’s three laws.

• Newton’s Law of Universal Gravitation can be stated as:

Every particle in the universe attracts every other particle with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between them. This force acts along a line joining the two particles

• In mathematical form:

  • F_21=F_12=G(m1m2 / d^2)

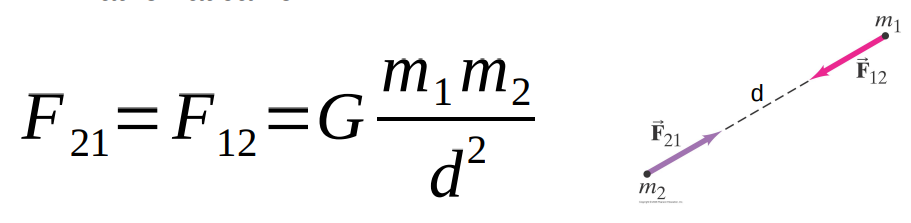
• G is a constant called Newton's Gravitational Constant, or Big G, and has a SI value of G = 6.67 x 10^-11 N m^2 / kg^2

• Gravity is quite different from the other forces we have met: it acts even though two objects are not in contact.

  • This is sometimes called Action At A Distance.

  • Something must happen to change the space between the two objects.

The gravitational force from a sphere

• Real objects are not points – they have finite size e.g. Earth.

• Newton was able to show that the force exerted by a sphere on a point object outside the sphere acts as if all the mass of the sphere were concentrated at its center.

• The force exerted by a uniform spherical shell upon a point object inside the shell is zero.

• This allows us to use Newton's Law of Gravitation – which is for point objects – for spherical ones.

• The distance d is the distance between the center of the sphere and the CM of the other object. The mass of the equivalent point object is the mass of the entire sphere.

EXAMPLE 1:

Which is stronger, Earth’s pull due to gravity on you, or your pull due to gravity on Earth?

• They’re the same.

EXAMPLE 2:

If the sun collapsed and became a black hole with the same mass, the Earth’s gravitational attraction to it would be:

• the same.

The mass of the Sun would be unchanged and the distance from the Earth also unchanged so the force of gravity from the Sun on the Earth would be unchanged.

Cavendish's experiment

• Henry Cavendish was able to prove Newton’s law experimentally on Earth.

  

The mass of the Earth

• Until Cavendish measured G the mass of the Earth was unknown.

• Newton's Law of Gravitation applies over all distances, even close to the surface of the Earth.

• Close to the Earth, we know the gravitational force acting on an object is its weight mg.

• The distance between the object and the center of the Earth is the radius of the Earth r E.

• From the values of g, G, and r E we find mE = 5.98 x 10^24 kg.

Earth's rotation and g

• The Earth's rotation changes the measured value of g over the surface of the Earth.

  • The net force on an object at the Equator cannot be zero.

A scale measures the force w = mg'

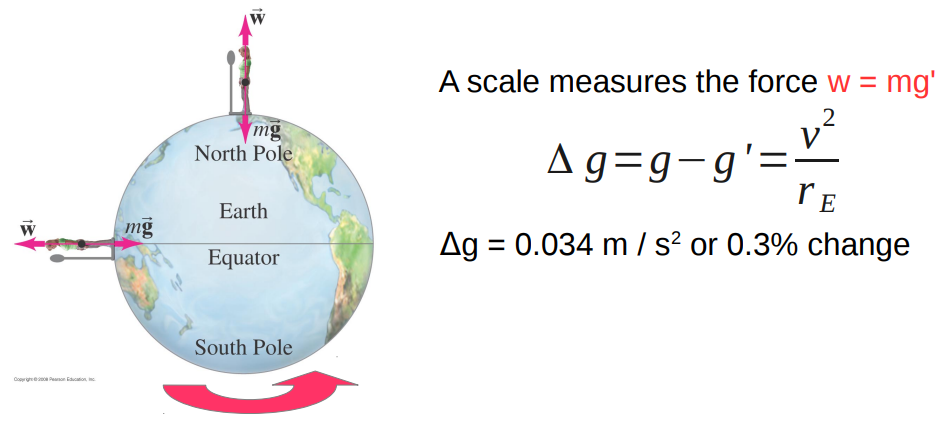
• The Earth's rotation is the reason the Mississippi flows from Minnesota to Louisiana and not the other way around.

  • Northern Minnesota is closer to the center of the Earth than Louisiana!

Satellites

• Gravity can be used as the centripetal force. Consider a satellite with mass mS orbiting the Earth of mass m_E.

• For a given velocity the height above the center of the Earth must be given by the above expression.

• The time it takes the satellite to complete one orbit is the period

  • 2πr=v T

• Solving for v and inserting into the previous equation we find

• 

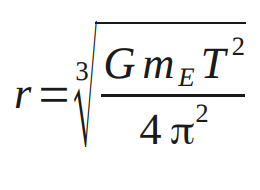
• A very interesting case is when T = 24 hours.

• Such a satellite would appear to be stationary above the Earth.

  • Such satellites are called geosynchronous or geostationary.

• Inserting the numbers for Earth's mass mE , G and T we find r = 42,300 km above Earth's center.

• This is about six times the Earth's radius.

• At this height v = 3.07 km/s.

Energy Conservation and Satellite Motion

• A satellite has a speed and is at a height above the Earth so it has a kinetic energy and a potential energy.

• Gravity is a conservative force so the mechanical energy of a satellite is a constant.

  • The sum of the KE and PE is constant at all points in the orbit.

• For a circular orbit, the potential energy is a constant so the kinetic energy is a constant which means the speed is a constant.

• 

• For an elliptical orbit, the distance above the Earth changes.

• The potential energy increases the further the satellite is from Earth.

• If energy is conserved, the kinetic energy must decrease to compensate.

• Thus the satellite moves at its slowest speed at the farthest point on the ellipse (the apogee) and at its fastest at the closest point (the perigee).

EXAMPLE 1:

Where is the maximum gravitational force?

• 

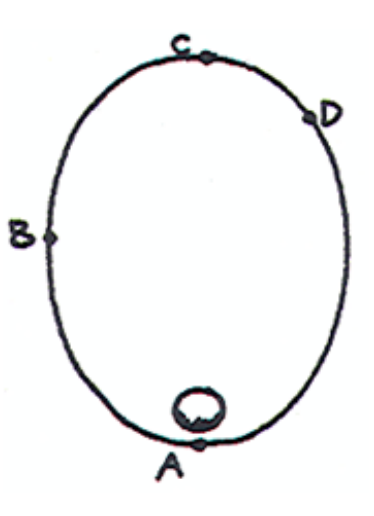
• A

EXAMPLE 2:

Where is the maximum speed?

• 

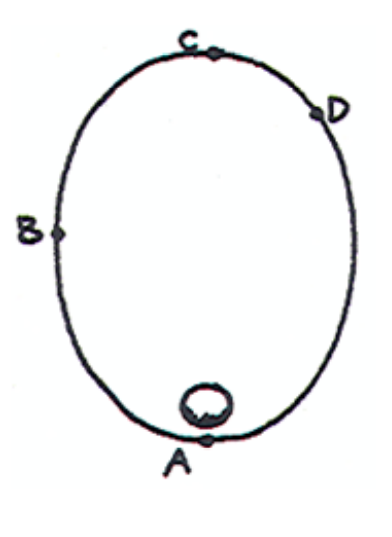
• A

EXAMPLE 3:

Where is the maximum gravitational potential energy?

• C

EXAMPLE 4:

Where is the maximum mechanical energy?

• Everywhere

Weightlessness

• Objects in orbit (such as astronauts) are said to be 'weightless'.

• This is obviously wrong: gravity is acting to keep them in their orbit.

• A better description is the object has 'apparent weightlessness'.

  • a scale registers zero weight

• The reason is the scale measures the normal force exerted by the object on the scale – not the object’s weight.

• In orbit, it is possible for the normal force to be zero.

• In order to experience true weightlessness an object has to be far from any other mass.

Tides

• Consider two real massive objects such as the Moon and Earth.

• The force of gravity decreases with distance from the source which means the force of gravity from the Moon on the Earth is not the same all over the surface of the Earth.

• Some places are closer to the Moon, some are farther away.

• The difference in the force of gravity over the surface of the Earth compared to the average is called the tidal force.

• Earth’s oceans and atmosphere (and to some extent its rocks) respond to this force and move.

• This is the cause of Earth’s tides.

• The Moon also feels tidal forces from the Earth. The shape of the Moon is distorted along the Earth-Moon direction.

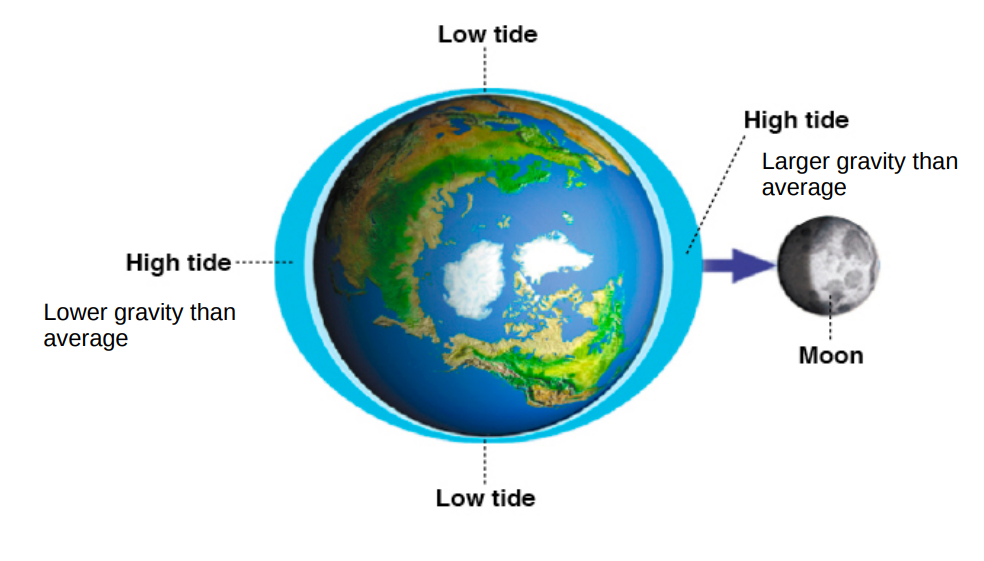
• The tidal forces from the Sun on Earth are smaller.

  • The Sun is farther away than the Moon.

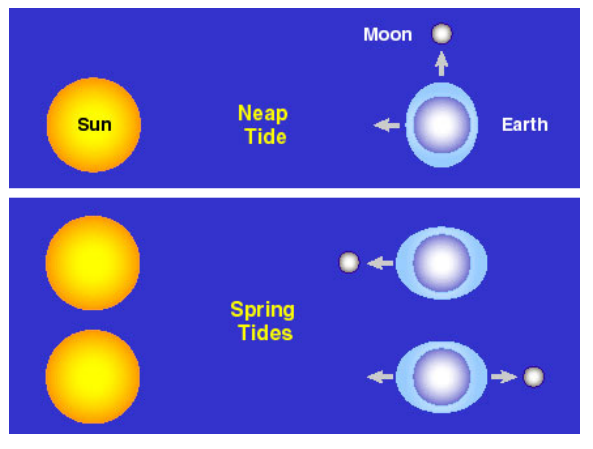
• When the Earth, Moon and Sun are at 90 degrees, the tides are smaller: these are called neap tides.

• When the Earth, Moon and Sun are aligned the tides are particularly strong: these are called spring tides.

  

The solar system and beyond

• The gravitational force from the Sun is the centripetal force that keeps the planets in their orbits.

  • Gravity is also the centripetal force which keeps the solar system orbiting in the Milky Way.

  • The gravitational force holds the Milky Way to Andromeda

EXAMPLE 1:

If the Sun were to suddenly disappear, what would happen to the Earth?

• It would fall out of orbit and spin into space.

Gravitational Fields

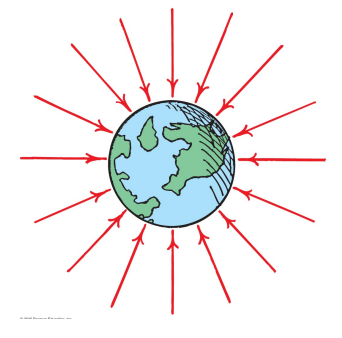
• The pre-Einsteinian view of gravity is that mass creates a ‘gravitational field’ around itself.

  • This is the same idea as magnetic or electric fields.

  • The field is the acceleration due to gravity g around that mass.

• Other masses ‘feel’ the field wherever they are.

  • If the mass is m then the force of gravity on that object is mg.

• Force fields are often represented by field lines.

  

Spacetime

• Not everything could be explained by Newton’s Law of Gravity.

  • There were errors in the prediction of the orbit of Mercury.

  • It also violated causality – the speed of gravity was greater than the speed of light.

• Albert Einstein proposed a new theory of gravity called General Relativity.

  • His predictions for the orbit of Mercury matched observations.

• Relativity had as large an impact upon philosophy as Newtonian Synthesis.

• Einstein predicted, among other things, that light grazing the surface of the Sun would be bent – gravitational lensing.

  • This was observed during a solar eclipse shortly afterwards.

• He also predicted the existence of gravitational waves.

  • These are distortions of spacetime which move like waves.

  • Gravitational waves were detected in 2015.

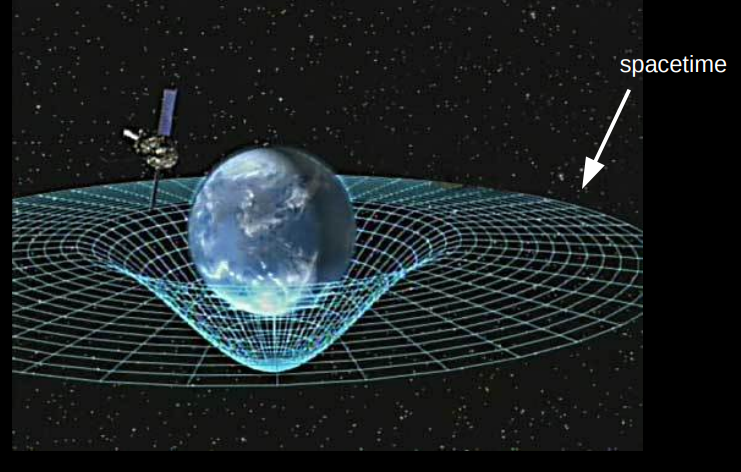
• The Einsteinian view of gravity is that mass distorts (warps) the space (and time) around itself.

• The trajectories of other masses in the warped spacetime differ from straight lines i.e. it looks like a force is being applied.

  

Black Holes

• If you project an object up from Earth with enough initial speed it will never fall back down.

• The minimum initial speed that leads to an object never falling down is called the escape velocity.

  • For Earth the escape velocity is 11.2 km/s = 25,000 miles per hour

• If you fix the mass of the object you’re trying to escape from then as the radius of that object decreases, the escape velocity increases.

• Below some particular size the escape velocity becomes larger than the speed of light.

  • The speed of light is the fastest speed anything can have,

• Such an object is called a black hole.

  • Even light cannot escape a black hole.

• The radius from the black hole where the escape velocity is the speed of light is called the event horizon.

• For many years there was good, but not conclusive, evidence for the existence of black holes.

• In the past decade the evidence became irrefutable.

  • We can now watch stars in the center of the Milky Way orbit the supermassive black hole that exists there.

  • We have taken a picture of the black hole in the middle of a nearby galaxy called M87.

• Since 2015 we have been detecting the gravitational waves emitted during the merger of two black holes.