Long Division

• We can divide polynomials by using long division

• Restrict the divisor - stating restrictions, make the divisor = 0 and solve

The Process of Long Division

1. Divide

2. Multiply

3. Subtract

4. Bring down

Non-polynomial long division example:

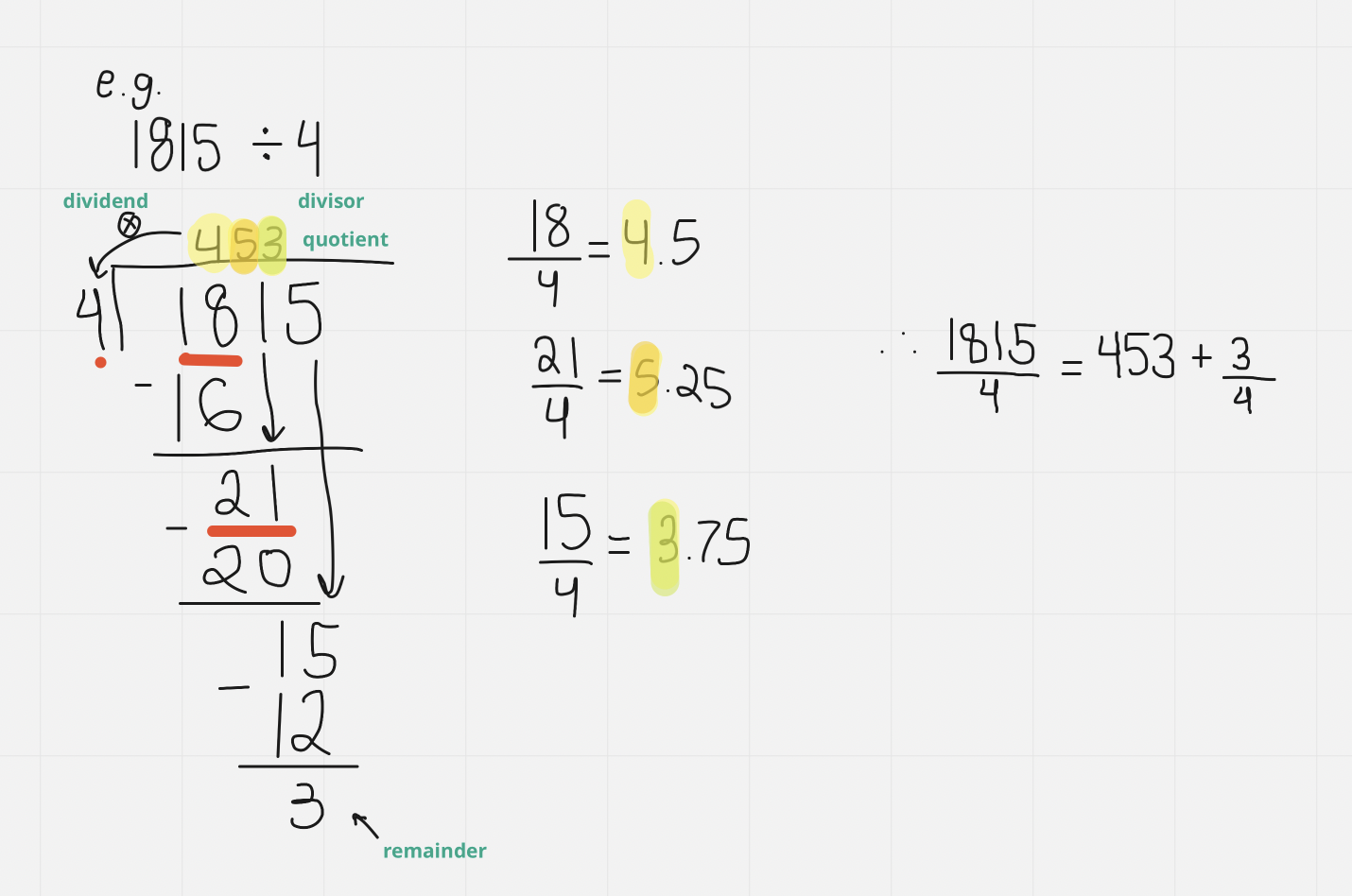
Quotient form

Check, clear fractions

Remainder Theorem

• Allows for us to determine the remainder without doing long division

When a polynomial function P(x) is divided by (x-b)→ P(b) = R

When a polynomial P(x) is divided by (ax-b) → P(b/a) = R

• Essentially, when you are dividing by variable added or subtracted with something, then you move it over and solve (because it originally must equal zero) and once you plug whatever you have just solved for into the equation, you will get the remainder

  • If x has a coefficient, then it becomes the denominator as you must divide it off to isolate x

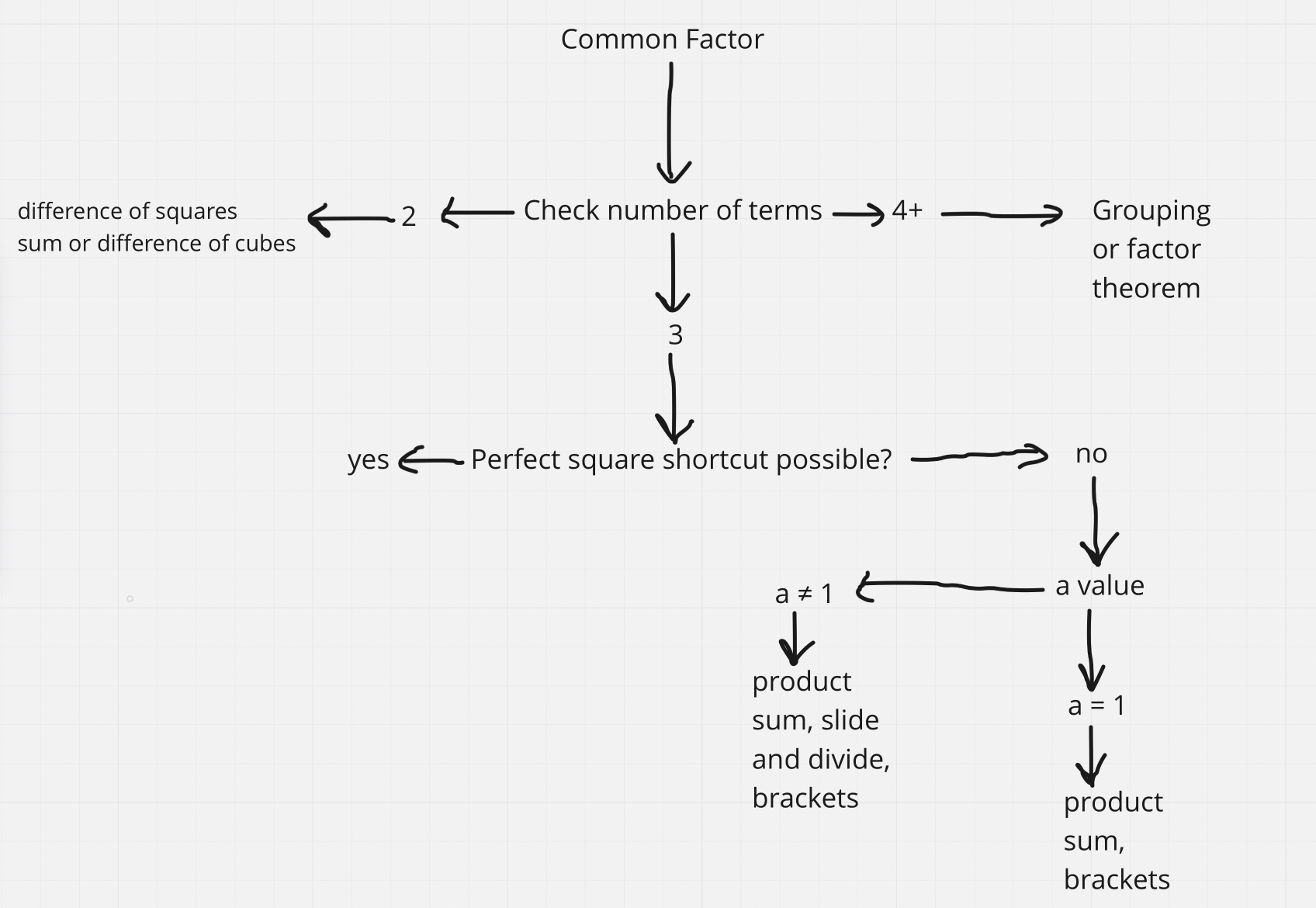
Types of factoring

Taking out a common factor

• Always do this first

Factoring Formulas

a² + 2ab + b² = (a+b)²

a² - 2ab + b² = (a-b)²

a² - b² = (a+b)(a-b)

a³ - b³ = (a-b)(a²+ab+b²)

a³ + b³ = (a+b)(a² - ab + b²)

Factor Theorem

Factor theorem states that…

x-b is a factor of a polynomial p(x) if and only if → p(b)=0

ax-b is a factor of a polynomial p(x) if and only if → p(b/a) = 0

Integral Zero Theorem

If x-b is a factor of polynomial p(x) with leading coefficient 1 and remaining coefficients that are integers then…

b is a factor of the constant

e.g.

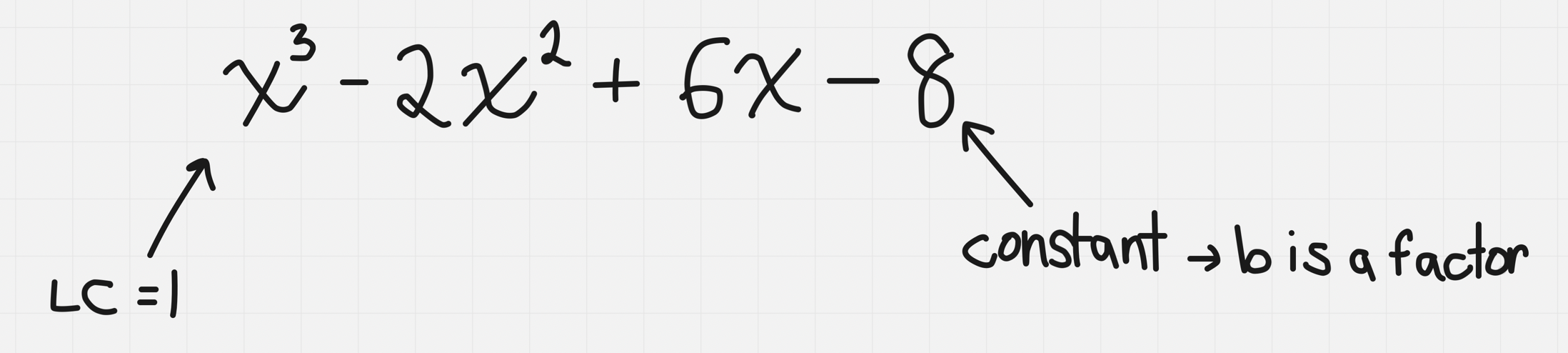
Rational Zero Theorem

If polynomial p(x) has integer coefficients and x = b/a is a rational zero of p(x), then….

• b is a factor of the constant

• a is a factor of the LC

• ax-b is a factor

  • Possible factors (test values) are any combination of ± b/a

Steps to Solving These Types of Problems

1. Find factors of a (LC) and b (Constant), both positive and negative (±)

2. Test p(b/a) until we get zero as a result of plugging (b/a) into the p(x) original equation → this is a factor, and we need to change it into an “unsolved” equation (e.g. x=1 would be (x-1) if you unsolved it, and thus your factor)

3. Divide by our factor using long division or synthetic division, you must get a remainder of 0

4. Take the factor found in step (2) and the quotient found in step (3) and smoosh them together

5. Factor fully from both brackets, and solve if needed

e.g.

Finding the Real Roots

The real roots of a polynomial equation can be found by setting the equation to zero, y=0

• If the polynomial is factorable, the roots can be determined by factoring first fully and then setting each individual factor bracket to zero

  1. Factor

  2. Solve each root

Families of Polynomial Functions

• Family: a group of functions with common characteristics (e.g. same x intercepts could be a common characteristic)

An Equation for the Family of Polynomial Functions with Zeros a₁, a₂, a₃…. aₙ

f(x) = a(x-a₁)(x-a₂)(x-a₃)…(x-aₙ)

a is different for each member of the family

The equation for a family can be determined from the zeros (x int) and a specific member of the family can be determined if given a specific point on the function

• Sub in (x,y) to find a, must know a point on the curve’s coordinates in order to do so

Solving Inequalities

• Sometimes there is a range of answers

• Polynomial inequality: when the equal sign (=) is replaced with an inequality

  • , <, ≥, ≤ are all inequalities

Solving with Inequalities

1. Isolate for x

2. Treat the inequality almost like an equal sign

   e.g.

3. 

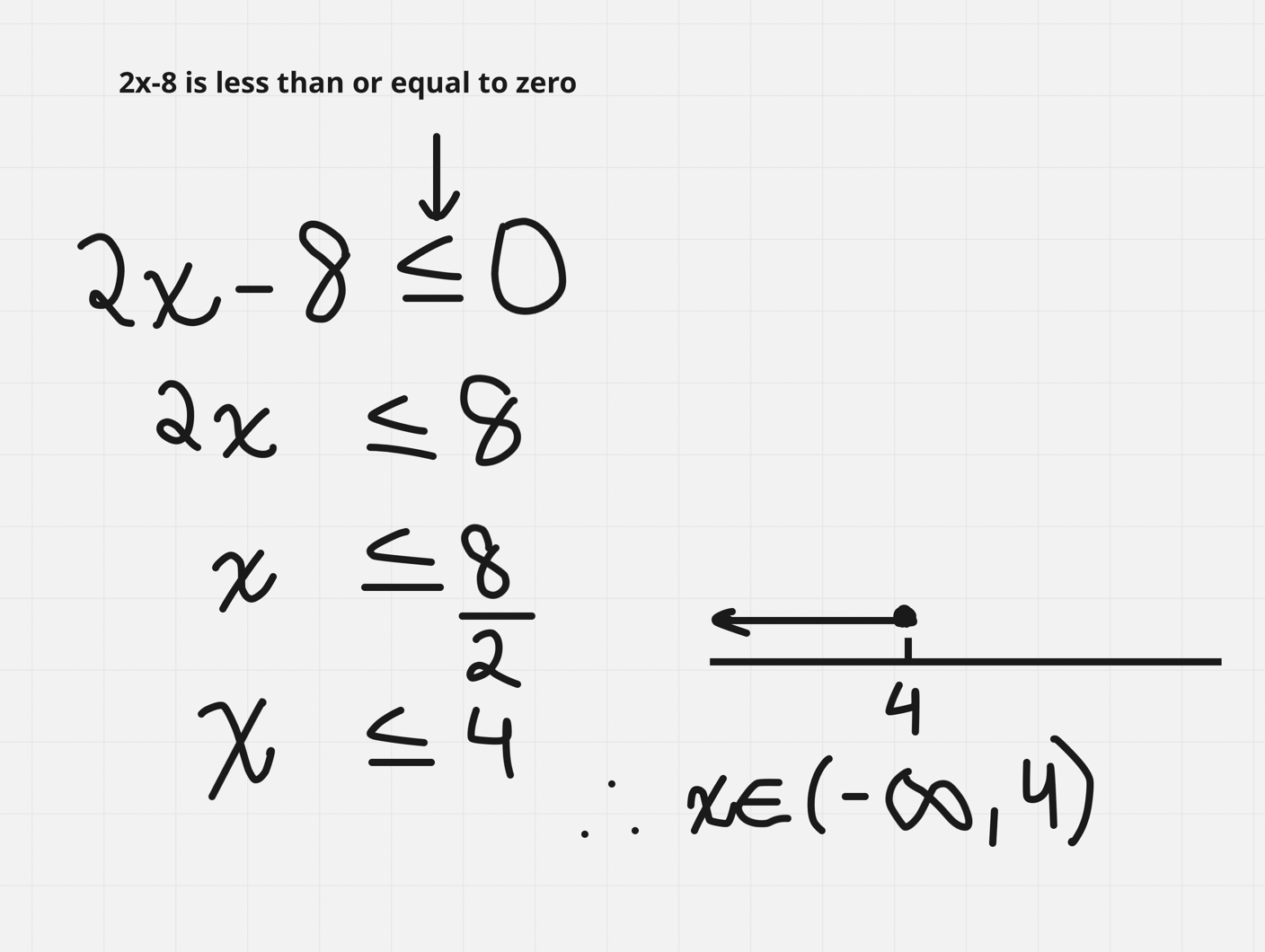
• The difference between = and an inequality: If we multiply or divide by a negative number in an inequality, we must flip or reverse the inequality

  e.g.

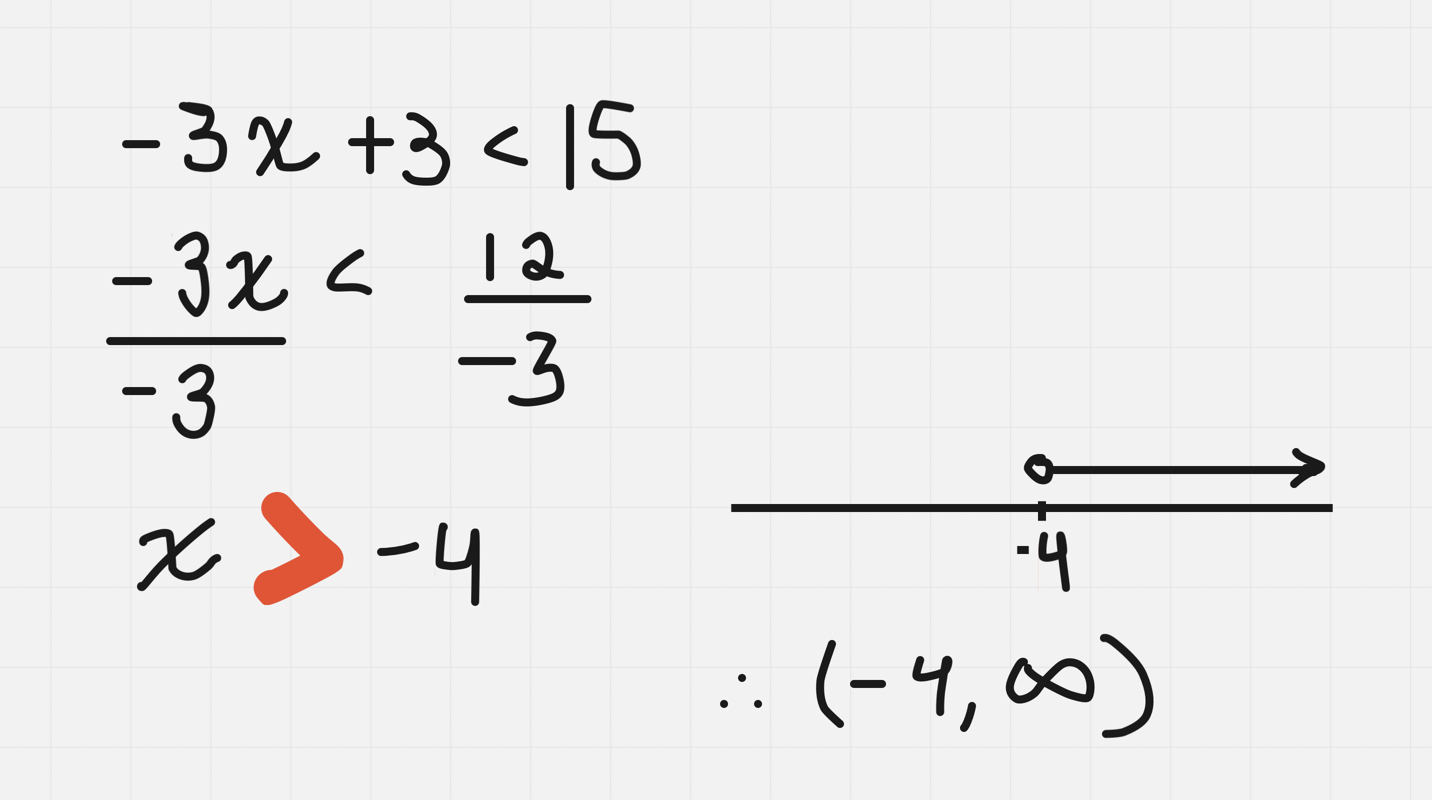
Interval Tables

• Always use circle brackets

1. Factor

2. Solve the brackets

3. Draw a number line to identify the intervals

4. Create a chart

   1. Place intervals in the chart as columns

   2. Place factors in the chart as rows

   3. Place a final function sign row at the bottom

5. Pick a random number in between the intervals (not including the written numbers as those aren’t included, we used circle brackets) and substitute it into the variable in each factor row put in → write the sign of the number that you get

6. Determine the final sign by multiplying all of the signs down to get the overall functions sign

   • 2 negatives make a positive, 2 positives make a positive, a mix of negative and positive makes a negative

7. Write your final X E statement based on what your looking for, and remember to put U in between intervals if there is more than one