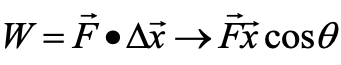Power, Work, and Energy
WORK
In Physics, the amount of force you exert is not the sole factor to determine whether or not work was done. It is more important to determine whether the force exerted was able to displace or move the body you’re applying the force on to
With this, we surmise that work can be defined in terms of applied force AND the displacement that it creates.
These are three conditions that must be met for work to be done:
- There must be a force acting on the object
- The object must be displaced
- The direction of the displacement must be the same as the direction of the force acting upon the object.
Work can be defined in terms of applied force and its displacement.
In detail, the work W done on an object by an applied force is defined as the product of the force and the displacement through which the force acts (Padua and Crisostomo, 2003). In equation form:
where W is for work, F is the force parallel to the displacement and d is the displacement.
| W = F . d |
|---|
The force exerted on the object is measured in newtons (N). The displacement is measured in meters (m).
Therefore, the amount of work is measured in newtons-meters. (N ⋅ m) or simply joule (J), named after James Prescott Joule, who has great contributions on understanding the concepts of work and energy. Work can also be measured in other units as shown in the table below.
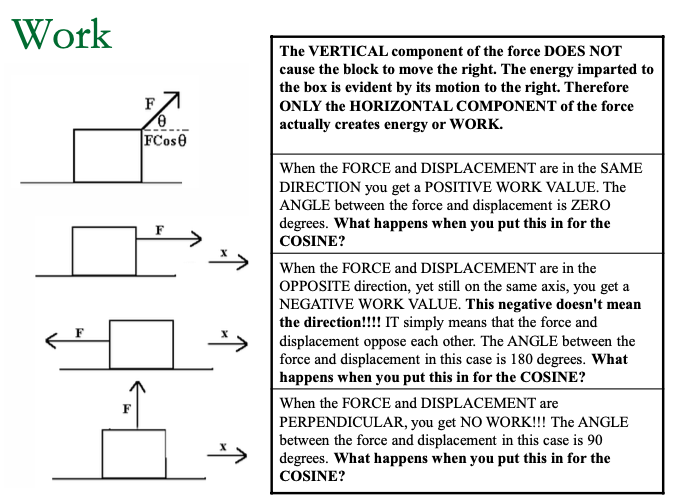
Work is a scalar quantity since it is a dot product of two vectors. Although work is a scalar quantity, it can be positive, negative, or zero.
It is positive when the component of the force is in the same direction as the displacement like a box being lifted from the ground. The direction of the force applied on the box, which is the upward direction is the same as the direction of the displacement.
It is negative when the component of the force is in the opposite direction as the displacement like a sliding book on a tabletop moving to the right. The frictional force is opposite to the direction of the sliding book. It is zero when the force is perpendicular to the displacement as described in activity number 2 items 3 and 5. Remember, the positive and negative sign does not refer to the direction of the work.
Work = The Scalar Dot Product between Force and Displacement.
- If you apply a force on an object and it covers a displacement IN THE DIRECTION OF THE FORCE you have supplied ENERGY to, or done WORK on, that object.
SCALAR DOT PRODUCT
- A product is obviously a result of multiplying 2 numbers. A scalar is a quantity with NO DIRECTION. So basically Work is found by multiplying the Force times the displacement and result is ENERGY, which has no direction associated with it.
<<W<< <<= Fx<< <<Area<< <<= Base x Height<<
A dot product is basically a CONSTRAINT on the formula. In this case it means that F and x MUST be parallel. To ensure that they are parallel we add the cosine on the end.
ACTIVITY
Study the following situations enumerated below. Put a check mark before the item if work is done to an object or person.
- %%A box being lifted from the ground.%%
The work is done on the box since there is applied force and displacement, where force is parallel to the displacement, as the box being lifted from the ground satisfying conditions 1, 2, and
%%A student walking up the stairs%%
==A waiter carrying a loaded tray in his steady arm across a room at constant speed.==
There is no work done by the waiter as he carries the loaded tray since the force applied is not parallel to the displacement.
%%A book falls off a table and free falls to the ground%%
==A girl whirling a small toy tied at the end of a string above her head==
there is no work done by the girl on the small toy since as the small toy is being whirled, the centripetal force acting on it is perpendicular with its displacement. \n
\n
POWER
Based on the definition of work, it does not matter how long it takes to do the work. You will do the same amount of work whether you walk up the stairs or run up the stairs.
\n
But why do you think you are more tired after running up the stairs than of walking up the stairs? To answer this question, you must need to understand the rate of doing work, which is termed as power (P). In equation form:
\n
| P = work done time |
|---|
You spend more power in running up the stairs since you used a larger amount of work in a short time so you get more tired. Similarly, some machines are more powerful than others since they can perform work faster. Remember that power and time are inversely proportional.
Power is also a scalar quantity. Its unit is joule per second (J/s) or simply watt ***(W)***.
- (In honor of James Watt, the developer of the steam engine).
The table below contains units of power in different systems of measurement.
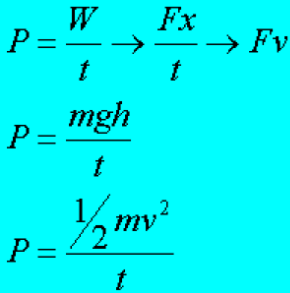

\n
ENERGY
is the physical quantity that ==enables a person or an object to do work.==
Without it, it is impossible for a person or object to do work. In short, energy is the ==ability to do work.==
A student can climb up a staircase because he has the capability to do so. Similarly, a machine can do some work because it has the capacity to do so.
Energy is the physical quantity that enables a person or an object to do work.
Without it, it is impossible for a person or object to do work. In short, energy is the ability to do work.
Like work, energy can be measured in joule (J)
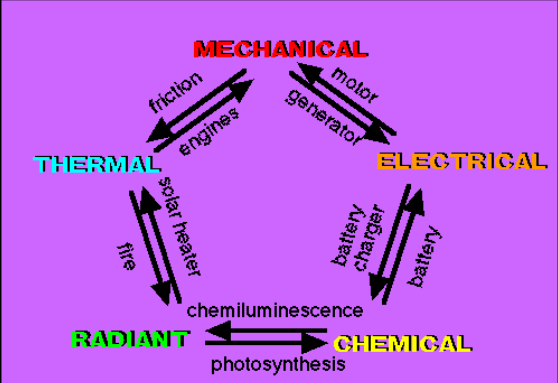
Energy comes in many forms but for now let’s have the two common forms of mechanical energy, which is the energy possessed by an object due to its position or due to its motion.
Running water has energy that is used to run water mills. Moving air has energy that pushes the sailing boats. These objects have energy because ==they are moving and the energy possessed by moving bodies is called== kinetic energy.
Water behind a dam has energy that once the dam is open, the water will flow that can move or carry objects. A child at the top of the slide has energy and when the child desires he can slide.
The energy in this object and person is stored energy. They can use this energy to perform work and the energy possessed by a body due to its position or condition is called potential energy
Types of Potential Energy:
Gravitational Potential Energy
is potential energy due to an elevated position
Elastic Potential Energy
is potential energy that depends on the amount of stretch of the material.
A rock gains gravitational potential energy when you lift it from the ground and a bow string gains elastic potential energy when you draw the bow.
Remember that when one does work, energy is transferred and when energy is transferred, work is done.
- For example, the water behind a dam has potential energy and that potential energy will be converted to kinetic energy as the dam opens and the kinetic energy of running water does the work for the water mills to run.This concept is known as work-energy principle
4.19 J = 1 calorie
Energy can be expressed more specifically by using the term WORK(W)
| KE | Kinetic Energy | 1/2 mv^2 |
|---|---|---|
| PEgrav | Potential Energy (gravitational) | mgh (mass. agravity . height) |
| PEelas | Potential Energy (elastic) | 1/2 kx^2. (k = spring constant x = distance |
As mass and velocity increase, KE also increases







| SUMMARY |
|---|
The motion of the object can be analyzed using the concept of work, power, and energy.
Work is done when these conditions are met a) there must be force acting on the object, b) the object must have displacement, and c) the direction of the displacement must be the same with the component of the force applied on the object.
Power is the amount of work done per time it takes to do it.
Energy is the capacity to do work. Kinetic energy is energy possessed by moving bodies and potential energy is a stored energy.
Work Energy Theorem
It basically means that if we impart work to an object it will undergo a CHANGE in speed and thus a change in KINETIC ENERGY. Since both WORK and KINETIC ENERGY are expressed in JOULES, they are EQUIVALENT TERMS!
" The net WORK done on an object is equal to the change in kinetic energy of the object."
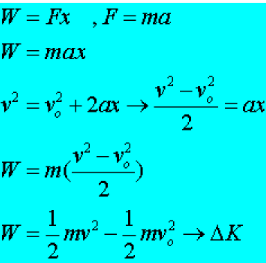
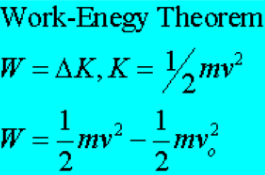
Lifting mass at a constant speed
Suppose you lift a mass upward at a constant speed, deltav = 0 & deltaK=0. What does the work equal now?
Since you are lifting at a constant speed, your APPLIED FORCE equals the WEIGHT of the object you are lifting.
Since you are lifting you are raising the object a certain “y” displacement or height above the ground.
When you lift an object above the ground it is said to have POTENTIAL ENERGY
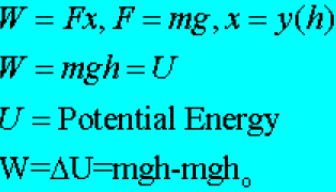
Suppose you throw a ball upward
What does work while it is flying through the air?
GRAVITY
Is the CHANGE in kinetic energy POSITIVE or NEGATIVE?
NEGATIVE
Is the CHANGE in potential energy POSITIVE or NEGATIVE?
POSITIVE
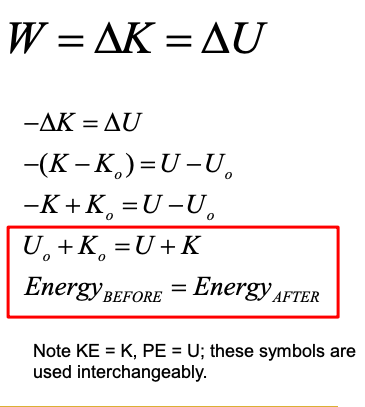

Springs - Hooke’s Law
Hooke's Law describes the force needed to stretch an elastic object. This is primarily in reference to SPRINGS.
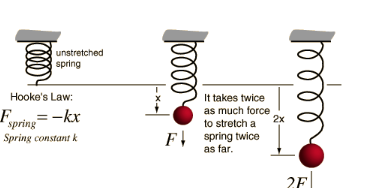

The negative sign only tells us that “F” is what is called a RESTORING FORCE, in that it works in the OPPOSITE direction of the displacement.
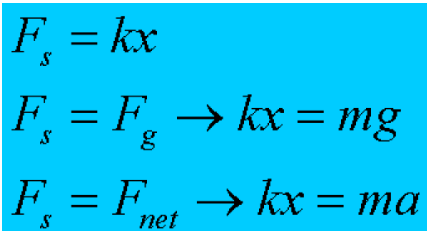
Elastic Potential Energy
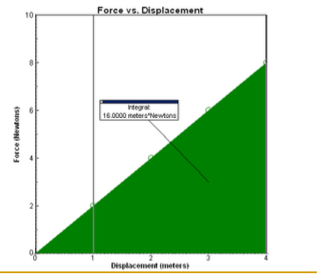
The graph of F vs.x for a spring that is IDEAL in nature will always produce a line with a positive linear slope. Thus the area under the line will always be represented as a triangle.
NOTE: Keep in mind that this can be applied to WORK or can be conserved with any other type of energy.

Heat and Temperature
Internal Energy - the sum of all the kinetic and potential energies of the components of the system
- -the energy that results from heat flow
Temperature - measures the average K.E of individual particles
Heat - the movement of thermal energy from a substance due to temperature difference
- -heat flows from a body of higher temperature to one at a lower temperature
Hence, a substance does contain internal energy but not heat.
HEATING CURVE
Latent Heat - Amount of thermal energy absorbed or released at constant temperature changing a substance phase
= J/g or kJ/kg
Latent Heat Of Fusion - the heat absorbed or released when matter melts, changing phase from solid to liquid form at a constant temperature.
Latent Heat of Vaporization - the heat absorbed or released when matter vaporizes, changing phase from liquid to gas phase at a constant temperature
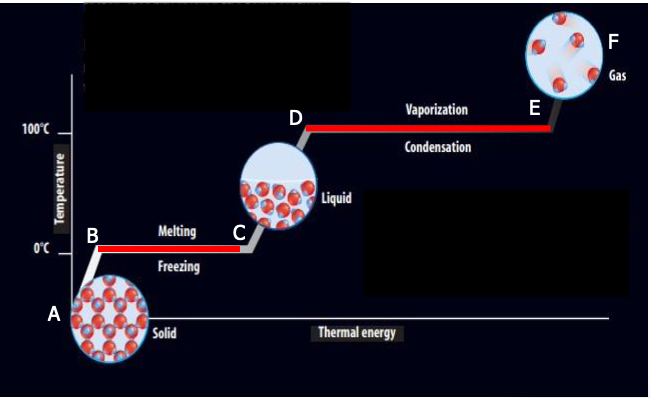
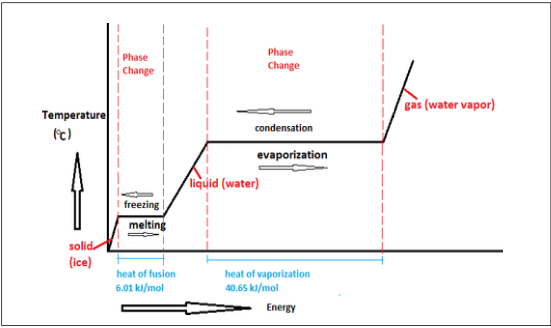
The heat that changes the temperature is sensible heat, the heat that changes the phase is latent heat.
PHASE DIAGRAM
- is a graphical representation of physical states of the substance under various conditions of pressure and temperature
Regions - phases (stable at this range of P&T)
Lines - two phase equilibrium boundaries (two phases can coexist)
Points
- Triple Point - all three phases can co-exist
- Critical Point - Highest P&T at which there is boundary between liquid and gas
AF
UNCOMMON TERMS
- Transpiration - helps the plant by providing evaporative cooling, nutrient uptake, and carbon dioxide entry
- Guard Cells -