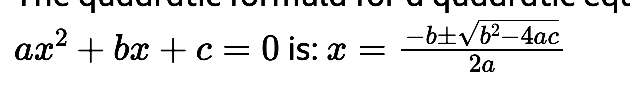Notation, vocabulary, and manipulation

Algebraic Expressions

• Variables are letters that represent unknown values or values that can change

• Terms are numbers or letters on their own, or numbers and letters multiplied together, and are separated by a + or - sign (Ex. -2, 3x, and 5x² are all terms)

• Expressions are terms put together using + or - signs (Note: Expressions don’t have an = sign) (Ex. 4x-3 and are both expressions)

• Equations are two expressions set equal to each other using an = sign. This tells us that both sides have the same value. (Ex. )

How to Simplify Expressions

• Like terms are terms that have the same variable raised to the same power (aka exponent), meaning that they are “like” each other and are used to simplify expressions (Ex. and are like terms)

• You simplify expressions by combining like terms, which means you add the coefficients (the numbers in front of the variables) of the terms while keeping the variable the same (Ex. and can be simplified into because the coefficients of 5 and -13 add to result in -8)

  • Ex.

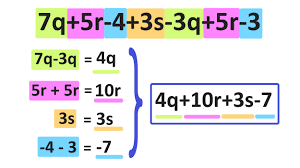
• Use the acronym PEMDAS (also called GEMDAS or BIDMAS) to know the order of operations if there are multiple like terms that need to be combined. Go in the order of each letter to know what to simplify first.

  • P (or G, or B)= Parenthesis (or Grouping symbols, or Brackets)

  • E (or I)= Exponents (or Indices)

  • M= Multiplication

  • D= Division

  • A= Addition

  • S= Subtraction

• For simplifying fractions, you can remove the highest common factors from both the numerator and denominator (just like simplifying fractions without variables)

  • Sometimes you may need to first factor the top and bottom of the fraction to find the common factors to remove

• You can only add or subtract fractions if they have a common denominator first, then you can add the numerators and keep the denominator the same

• To multiply fractions, just multiply the numerators and denominators together (just multiply straight across)

• To divide fractions: Keep, change, flip. Keep the first fraction, change the division symbol into multiplication, and then flip the top and bottom of the second fraction. Then solve by multiplying the fractions together.

How to Get Rid of Brackets

• If there is one bracket, Distribute= Multiply each term outside of the bracket to each term inside the bracket and then simplify

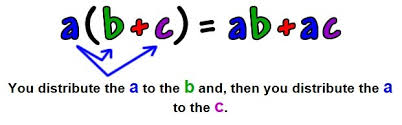
• If there are two brackets next to each other (Ex. ), you still multiply each term of one bracket by each term of the other bracket and then simplify. To make this easier you can use the acronym FOIL to help distribute and then you simplify.

  • F= First. Multiply the first two terms of each bracket together (Ex. )

  • O= Outer. Multiply the outer two terms of the brackets together (Ex. =15x)

  • I= Inner. Multiply the inner two terms of the brackets together (Ex. 6 7y= 42y)

  • L= Last. Multiply the last two terms of each bracket together (Ex. 63=18)

• If three or more brackets are being multiplied together, FOIL two of them and then multiply that result with the remaining bracket. Simply multiply each term of the brackets together. Then, simplify by combining like terms.

Algebra Rules for Proofs

Even and Odd

• 

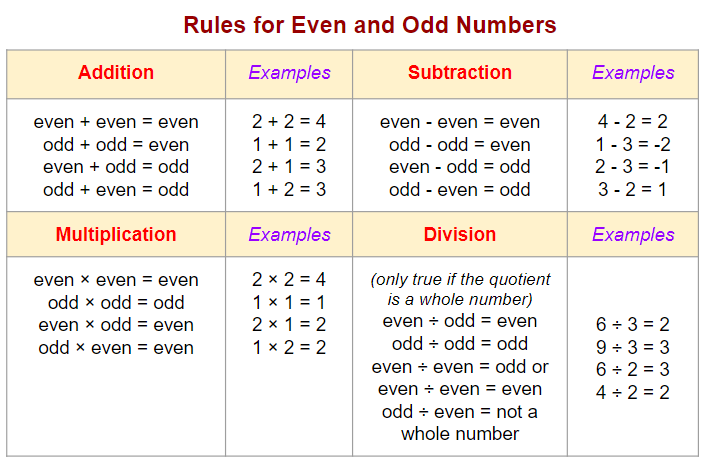
• Note: Division rules don’t always follow a certain rule, so always test out sample numbers

• Tip!: Test out various numbers in your equation if you can’t remember these rules (which you can use for proofs or to solve an equation)

• Also, if is an integer, an even number can be written as , while an odd number can be written as or

Consecutive Numbers

• Consecutive numbers are numbers that come right after one another (Ex. 4,5,6,7,…)

• If is the first integer (whole number), then you can write the consecutive integers as … and so on. This knowledge is helpful for proofs, for finding the values of consecutive numbers in a problem, and similar questions.

Factoring

• A quadratic equation (with an ) can be factored into (x+a)(x+b) form.

• Factoring can be done using the product and sum method which can be written as

• Pay attention to negative signs

• Note: Difference of Square Rule= If a quadratic equation is in the form x²-a², the factors will be (x-a)(x+a)

• When the coefficient of is not 1, then set up two brackets with factors of first term (Ex. if the coefficient is 6, you can set up the brackets like this: (2x+ )(3x+ ) ). Then, plug in factors of the last term in the quadratic and see if you can use the product and sum method to get the same quadratic you started with. You may have to guess and check, and try various factors together.

Formulas

• A formula is a mathematical rule or relationship that uses variables and is always true (Ex. )

• Substitution is when putting numbers in place of letters to calculate the value of an expression. Matching units of variables in the formula and in the problem can help determine which number goes in place of which variable.

• You can create formulas by assigning variables for different values and using the units of the values to determine how to put the numbers and variables together in order to get your equation in the units you desire

Rearranging Formulas

• The subject of a formula is the variable that is on its own on one side of the equals sign. The goal, when rearranging a formula, is to get the subject on one side of the equation by itself, meaning you have to use the opposite operation to move everything to the other side (opposite of addition is subtraction, opposite of multiplication is division).

• Remember, whatever you do to one side, you have to do to the other (subtract 1 from both sides in order to move it to the other side of the equals sign)

• Ex.

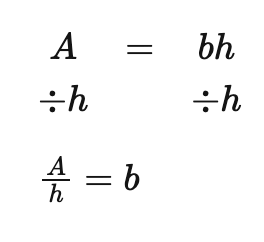
• Use the opposite order of PEMDAS (also called GEMDAS or BIDMAS) to know what order to perform your operations (start with S, then A, D…)

Composite Formulas

• Composite functions are when the output from one function is used as the input of another function, written as or , where the output of g(x) becomes the input (x) of f(x).

Graphs

• A coordinate is the position of a point on the graph written as (x,y).

• The origin of a graph is the point (0,0)

• Use units in order to understand the meaning of graphs

Transformations of Graphs

• A translation is a movement of the graph either horizontally or vertically

• Vertically: (outside of the x)

  • If is positive, then the graph moves up

  • If is negative, then the graph moves down

• Horizontally: (inside the x)

  • If is positive, then the graph moves left

  • If is negative, then the graph moves right

• Reflections:

  • -> Reflection over the x-axis

  • -> Reflection over the y-axis

Graphs of Lines

• Vertical lines are written in the form x=k while horizontal lines are written in the form y=c

• y=mx+c is the general equation of a straight line, where m is the slope or gradient of the line and c is the y-intercept

  • = change in y/change in x. If m is positive, the line is going up; if m is negative, the line is going down; if m is zero, there is no change (a flat line; horizontal)

• Two lines are parallel if they have the same gradient, meaning they will never intersect

• Two lines are perpendicular if they meet at a right angle, meaning that their gradients are negative reciprocals of each other and the product of those gradients will be -1

• To find the equation of a line: Find using the formula, then plug it into the y=mx+c equation. Use one of the points for the and values and then solve for . Now, write your equation.

Graphs of Quadratics

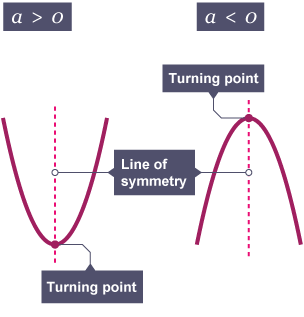
• (<- using the y=ax²+bx+c equation)

• The turning point is the vertex of the quadratic and is found by finding the x-value of the turning point using . Plug this x-value back into the equation to find the y-value of the turning point.

• The line of symmetry is the line through which the parabola is symmetric and always goes through the turning point, meaning you can use to find the line of symmetry (same x-value as the vertex)

• You can use the x-intercepts (solutions) to help graph the equation

Graphs of Cubics

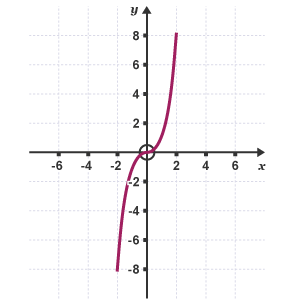
• (has in it’s equation)

Graphs of Reciprocals

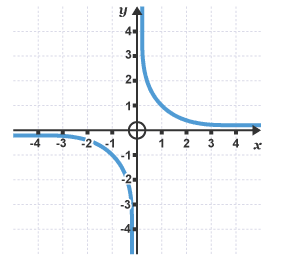
Graphs of Exponentials

• 

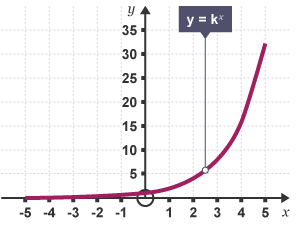
• These graphs never touch the x-axis; the y-value is never 0

Graphs of Circles

• The equation of a circle (with the center at the origin) is , with being the radius of the circle (Remember that the radius is half of the diameter)

• A tangent to a circle at point P is a straight line that touches the circle at only Point P and is perpendicular to the radius

  • To find the tangent line, use the slope of the radius to find the slope of the perpendicular tangent line, and then use the point to find the line.

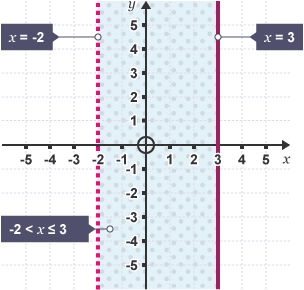
Graphs of Inequalities

• Dashed lines show < or > (solutions are not on that line) while solid lines show or (solutions are on this line)

• The shaded regions show all the values where the inequality is true (can be multiple)

• 

Solving equations and Inequalities

Solving Equations

• Solving an equation means finding the value(s) when the two expressions are equal, or what equals to make the equation true.

• To solve an equation, simply rearrange the equation to get the subject, which is x (or any other variable), on one side of the equation. Use the opposite order of PEMDAS (also called GEMDAS or BIDMAS) to get x by itself on one side (start with S, then A, D…)

  • To check your answer, you can plug in the values that you found for your variables and see if your equation is true (solve it).

  • It’s easier to expand brackets and then solve.

• With brackets on both sides of the equation: expand the brackets, move the variable to one side, and then solve.

• With fractions: since fractions indicate division, use the opposite operation (multiplication) to get rid of the fraction, then solve.

Solving Two Equations (Simultaneous Equations)

• Substitution Method: Isolate one variable in one equation and plug it into the other equation. Solve for the variable that is left, and then use that value to find the other value. Best used when the coefficient of one variable is 1, or one equation already has one variable on one side of the =.

  • If there is a linear (y=ax+b) and quadratic equation (y=ax²+bx+c), substitute the , move the variables to one side and set it =0. Then factor, set each bracket=0, and solve.

• Elimination Method: Eliminate one variable from the equations, solve, and then use that value to find the value of the other variable. Best used when both the variables are on one side and have coefficients greater than 1.

  • Note: You sometimes have to multiply the equations by different numbers in order to get two coefficients that are the same number for the same variable to then eliminate (Shown in example)

• Ex.

• You can also solve graphically by drawing each line and then finding the points where the lines intersect

Solving Quadratic Equations

• Factoring: First set the equation equal to 0 (x²+7x+12=0), factor [(x+3)(x+4)=0], set each bracket equal to 0 (x+3=0 and x+4=0), and then solve for x (x=3,4). This is the most common and easiest method

• Quadratic Formula: Use when you can’t factor

  • 

• Completing the Square:

  • Also used when trying to find the value(s) of x in a quadratic equation that cannot be factored

Inequalities

• 

• When shown on a number line, closed circles are used for or , while open circles are used for < or >

Solving Inequalities

• Solve inequalities the same way you would an equation (but with inequalities) but watch your negatives

• The Negative Rule: When you multiply or divide an inequality by a negative number, you must flip the inequality (< turns into >, same for and )

• Inequalities likely have multiple answers so usually you can just list out some integer solutions

Sequences

• A sequence is a set of numbers (also called terms) that follow a pattern or rule.

  • An arithmetic sequence is when the rule is to add or subtract a number each time

  • A geometric sequence is when the rule is to multiply or divide a number each time

  • A linear sequence is one which increases or decreases by the same amount each time

• The term-to-term rule of a sequence describes how to get from one term to another (Ex. add 4)

• Each term in a sequence has a position, the nth position, where the first term has the first position and then it continues.

• To find the term when given the position for a linear sequence, make a table with the position in the first row and the term in the second row. Then, figure out what operations you need to perform in order to change the position number into the term number. Do those same operations to the variable , and then you can find any number of that sequence using its position.

  • Ex.

Quadratic Sequences

• Quadratic sequences are identified by the fact that their first differences are not equal but their second differences are equal

  • Ex.

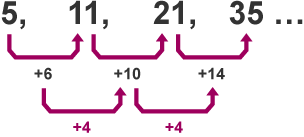
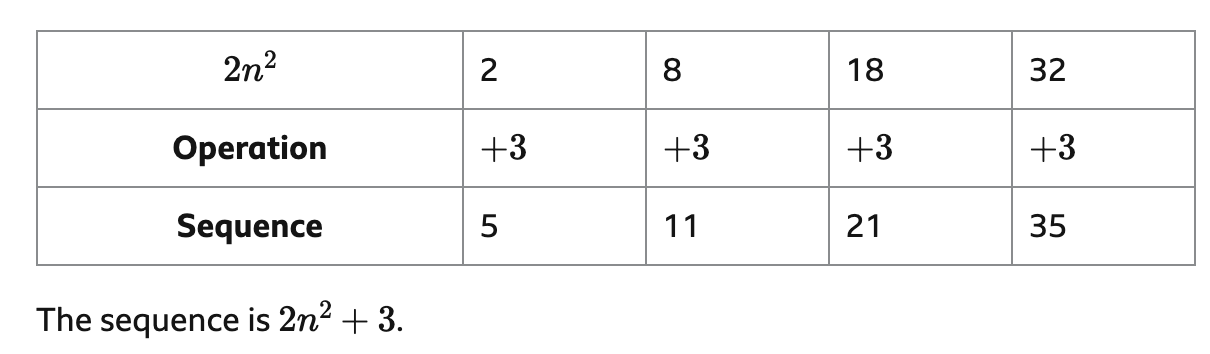
• To find the term when given the position for a quadratic sequence, you follow the same idea as if it were a linear sequence except for your position row which will now be squared (, with the coefficient of being half the second difference number. Make a row with the coefficient and follow the same process of finding operations. You then write that with the coefficient .

  • Ex.

Special Sequences

• Square numbers: 1, 4, 9, 16, 25, 36,...- the nth term is

• Cube numbers: 1, 8, 27, 64, 125,... - the th term is

• Triangular numbers: 1, 3, 6, 10, 15,... (these numbers can be represented as a triangle of dots)

  • The term to term rule for the triangle numbers is to add one more each time: 1+2=3, 3+3 = 6, 6+4=10, etc. The nth term is [n(n+1)]/2

• Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13…(in this sequence you start with 1 and 1 and then to get each term you add the previous two terms), 1+1=2, 1+2=3, 2+3=5, and so on.