Chapter 5: Continuous Random Variables

Introduction

Properties of Continuous Probability Distributions

• Probability density function: a statistical measure used to gauge the likely outcome of a discrete value

  • f(x) ≥ 0

  • The total area under the curve f(x) is one.

    

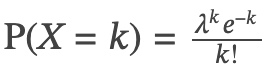
• Cumulative distribution function: a function whose value is the probability that a corresponding continuous random variable has a value less than or equal to the argument of the function.

  • P(X ≤ x) = (x−a)/(b−a)

5.1 Continuous Probability Functions

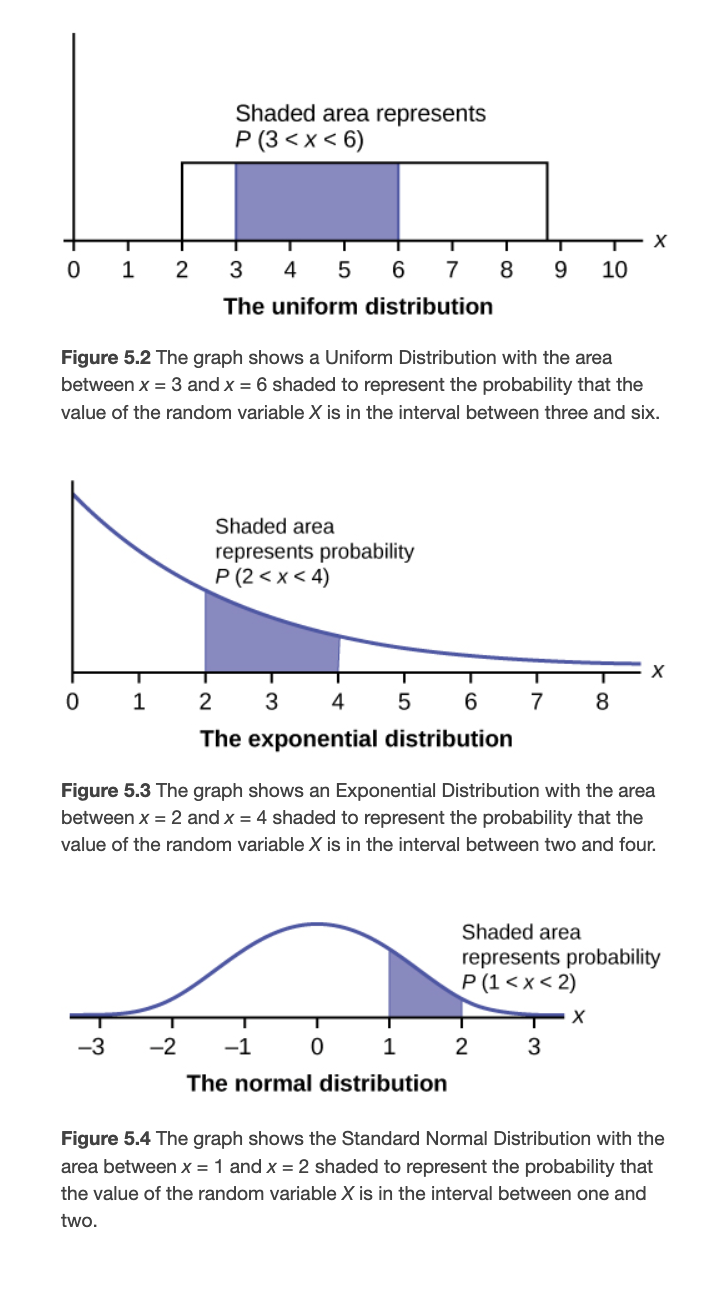
• Continuous probability distributions: PROBABILITY = AREA

• Continuous probability density function: gives the relative likelihood of any outcome in a continuum occurring

  • f(x)=1 / b−a for a ≤ x ≤ b

5.2 The Uniform Distribution

• The uniform distribution: is a continuous probability distribution and is concerned with events that are equally likely to occur.

  • Uniform Mean: 𝜇=(a+b) / 2

  • Uniform Standard deviation: 𝜎=√((b−a)^2 / 12)

  • Uniform pdf: f(x)=1 / b−a for a ≤ x ≤ b

  • Uniform cdf: P(X ≤ x) = x−a / b−a

• X = a real number between a and b (in some instances, X can take on the values a and b). a = smallest X; b = largest X

• Probability density function: f(x)=(1 / b−a) for a ≤ X ≤ b

• Area to the Left of x**:** P(X < x) = (x – a)(1 / b−a)

• Area to the Right of x**:** P(X > x) = (b – x)(1 / b−a)

• Area Between c and d**:** P(c < x < d) = (base)(height) = (d – c)(1 / b−a)

5.3 The Exponential Distribution

• Memoryless property: the independence of events or, more specifically, the independence of event-to-event times or P (X > r + t | X > r) = P (X > t) for all r ≥ 0 and t ≥ 0

• Exponential Distribution: X ~ Exp(m) where m = the decay parameter

  • decay parameter: m = 1 / μ and we write X ∼ Exp(m) where x ≥ 0 and m > 0

  • exponential pdf: f(x) = me^(–mx) where x ≥ 0 and m > 0

  • exponential cdf: P(X ≤ x) = 1 – e^(–mx)

  • exponential mean: µ = 1/m

  • exponential standard deviation: σ = µ

  • exponential percentile k: k = ln(1−AreaToTℎeLeftOfk) / (−m)

  • Additionally

    • P(X > x) = e^(–mx)

    • P(a < X < b) = e^(–ma) – e^(–mb)

• Poisson probability:  P(X=k)=𝜆^k e^−k / k! P(X=k) with mean λ

• k**!** = k*(k-1)*(k-2)*(k-3)*…3*2*1

Examples