Unit 2 - Circular Motion ! 🌀
Motion in two dimensions = Circular Motion
Is an object with constant speed that is accelerating towards the center of the circle
The object is accelerating because its velocity is changing as its direction of motion changes
Remember that velocity is a vector with both magnitude and direction, so when the direction of an object is constantly changing, leading to a net acceleration directed toward the center.
The acceleration vector a, points towards the center of the circle
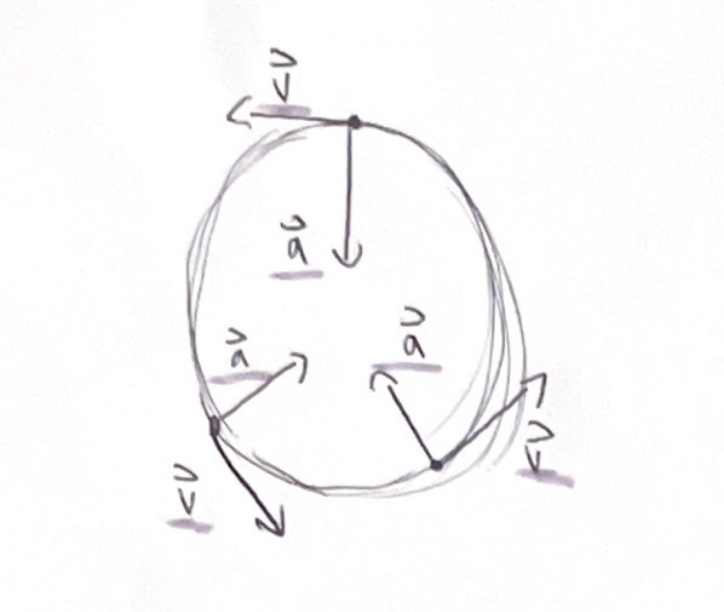
The velocity v, is always tangent to the circle and perpendicular to acceleration at all points
The acceleration a, always points towards the center of the circle
acceleration that always points towards the center of a circle is called centripetal acceleration
Not a new type of acceleration, only naming an acceleration that that corresponds to this specific type of motion
Magnitude of centripetal acceleration is constant because the change in velocity in the motion diagram has the same length
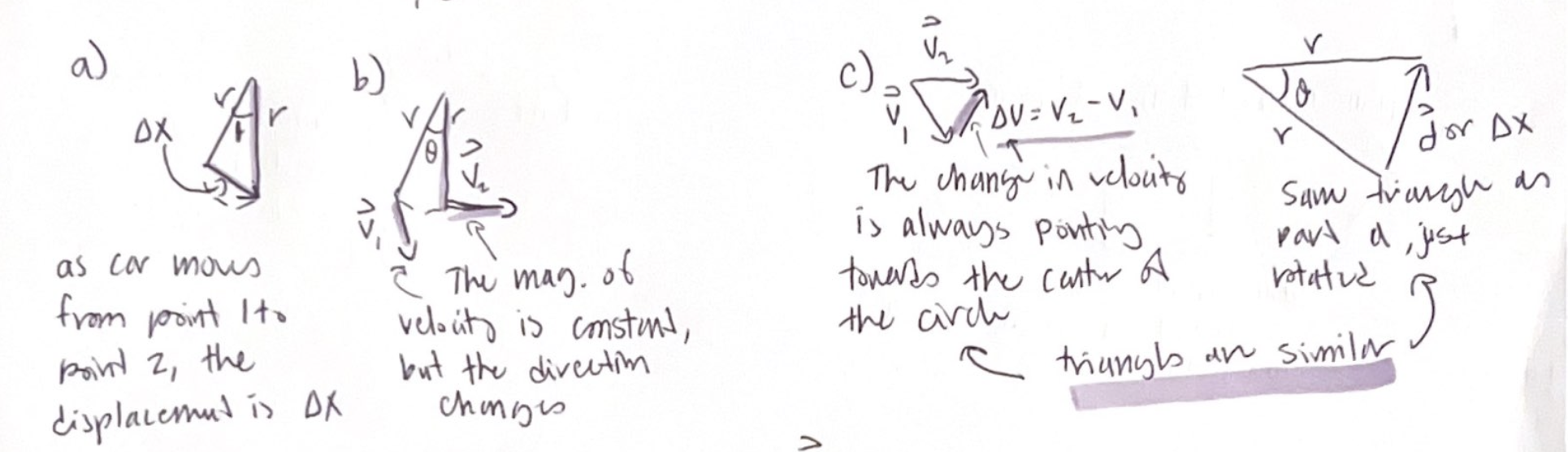
Figure C shows the vector calculation of the change in velocity
triangle is geometrically similar to the one that shows displacement
Recall from geometry that similar triangles have equal rations of their sides so we can write
Δv/v = d/r
Where Δv is the magnitude of the velocity-change vector. We’ve used the unsubscripted speed v for the length of the a side of the first triangle because it is the same for velocities v1 and v2
We know that displacement is written as Δx = vΔt
So we can substitute this for d in the equation Δv/v = d/r, giving us
Δv/v = vΔt/r
Which can then be arranged as
Δv/Δt = v²/r.
Remember form kinematics that acceleration is equal to the change in velocity over an interval of time so we are left with the equation
a = (v²/r, towards center of circle)
Looking at the equation, we understand that acceleration depends on the speed and the radius of the circle, creating a quadratic relationship
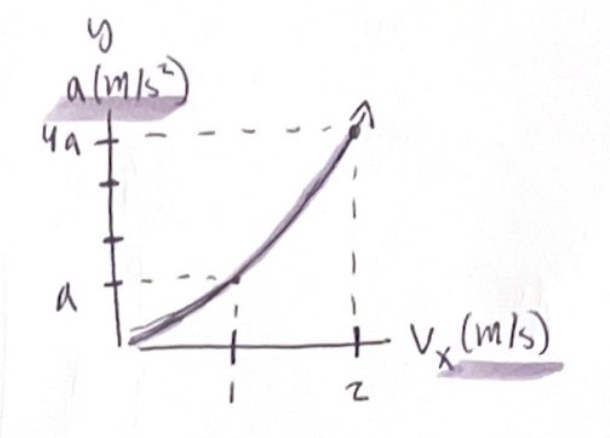
Acceleration is proportional to the square of speed, doubling the speed means a fourfold increase in acceleration
Ex. Child on a Swing

What change could the child make to increase the acceleration she experiences?
The radius of the circle depends on the length of the chain/rope and since you can't change its length, so the easiest way for the child to increase her acceleration would be to increase her speed
Uniform Circular Motion
Uniform motion requires an acceleration towards the center of the circle
This means that there must be a force directed toward the center of the circle
Cables on a carnival ride cause the tension force directed towards the center of the circle, this force keeps rider moving in a circle
Velocity and Acceleration in Uniform Circular Motion
Although speed of a particle in uniform circular motion is constant, velocity is NOT constant because the direction of motion is always changing
Acceleration depends on speed but also distance from the center of the circle
Acceleration is due to a change in direction not a change in speed
Matches your experience in a car: If you turn the wheel of a car to the right, your car then changes its motion towards the right, in the direction of the center of circle
Note! You can have uniform circular motion without completing a full circle, for instance, when a car turns at a constant speed around a curve, it continuously accelerates towards the center of the turn, maintaining its circular path.
Period, Frequency and Speed
In most cases, we will look at objects completing multiple full circles of motion, one after another
Since potion is uniform, each time around a circle is a repeat of the one before
This means that the motion is periodic
The time interval it takes an object to go around a circle one time, completing one revolution (rev), is called the period of the motion
Period is represented by symbol T
Rather than specifying the time for one revolution, you can specify circular motion by its frequency
Frequency is the number of revolutions per second
Represented by the symbol f
An object with a period of ½ seconds completes two full revolutions each second
If an object can make 10 revolutions in 1 second, then the period is 1/10th of a second
Frequency is the inverse of the period
f = 1/T
Revolutions are not true units but merely the counting of events
The SI unit of frequency is simply inverse seconds or s^-1
Could be given in revolutions per minute (rpm) or another time interval
Usually need to convert to s^-1 before calculations
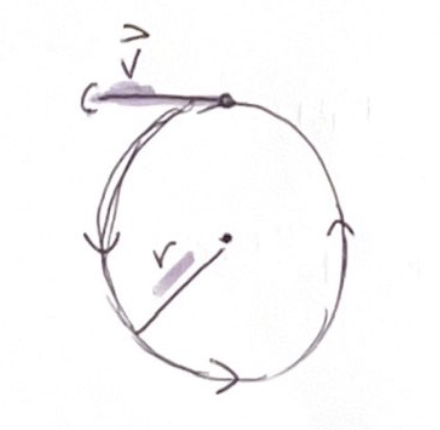
In one period T, the object travels around the circumference of the circle a distance of 2πr
We know time it takes for an object to travel one revolution is equal to its period and we know the distance traveled is 2πr
We can write an equation relating the period, the radius, and the speed
Remember that the period is the time it takes to make a full rotation or Δt
v = Δx/Δt = 2πr/T
Given equation f = 1/T relating frequency and period, we can rewrite this to be
v = 2πr/(1/T)
or
v = 2πfr
Combining this with acceleration (a = v²/r) you get an expression for the centripetal acceleration in terms of frequency/the period for the circular motion
a = v²/r → a = (2πr/T)² / r → a = (2πfr)² / r
or
a = (2π/T)²As acceleration increase the amount of time it takes to make a loop (T) decreases
This is because acceleration is the rate at which velocity changes, and a higher acceleration means the velocity changes more quickly, allowing the object to complete the loop in a shorter time.
2 circles per second = period of ½ rps
Dynamics of Uniform Circular Motion
Riders traveling around on a circular carnival ride are accelerating as seen before
According to newton's second law, Fnet = ma, the riders must have a net force acting on them
Fnet = ma (mv²/r, toward center of circle)
Net force producing the centripetal acceleration of circular motion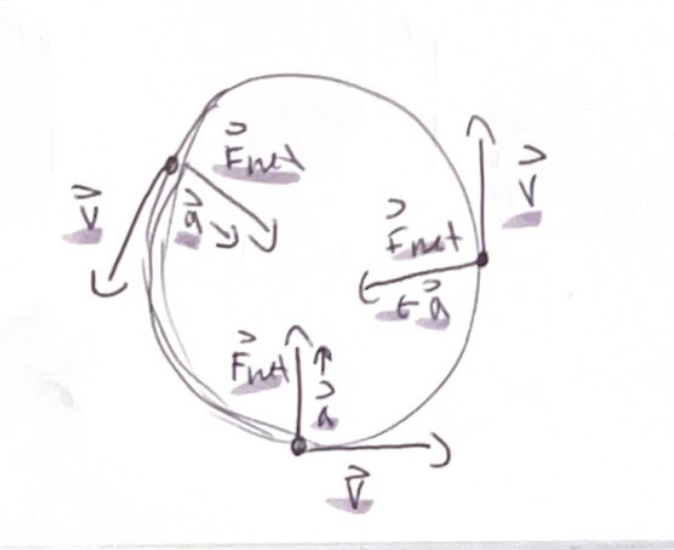
The net force required to keep the object motion in a circle is always directed towards the center of the circle
The net force causes a centripetal acceleration
A particle of mass m moving at a constant speed v around a circle or radius r must always have a net force of magnitude mv²/r, pointing towards the center of the circle
Net force causes the centripetal acceleration of circular motion
Without net force the particle would move off in a straight line tangent to the circle

Again not a new kind of force, the centripetal net force will be due to one of our familiar forces (tension, friction, normal force, ect)
Fnet = mv²/r tells us how the net force needs to act
how strong and in which direction to cause the particle to move with speed v in a circle of radius r
Need to consider a physical force or a combination of forces directed towards the center, causing acceleration when solving problems
Finding Maximum Speed
In physics, the relationship between Vmax and the coefficient of friction (μ) arises in situations involving motion on inclined surfaces or circular paths, where friction limits the maximum velocity.
Vmax, or the maximum velocity, is the highest speed an object can attain before slipping, sliding, or losing contact with a surface due to frictional forces.
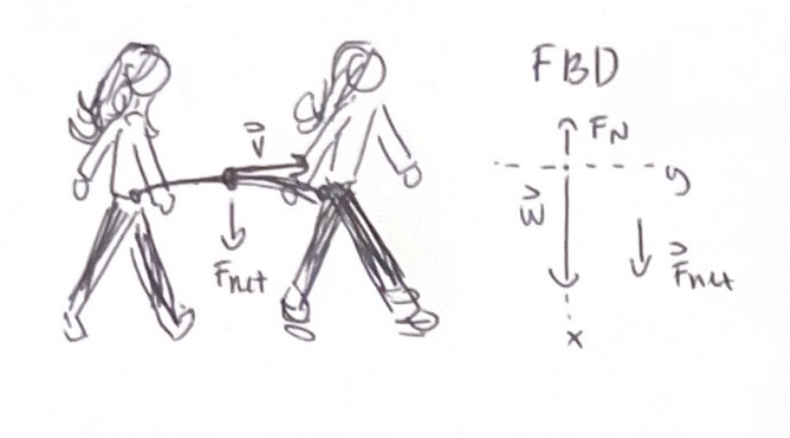
When walking, there is an upper limit to the speed that you walk, limit set by physics of circular motion
During each stride, her hip undergoes circular motion
Circular motion requires a force directed towards the center of the circle
The radius of the circular motion is the length of the leg from the foot to the hip
The path your body makes while taking a stride is the arc of the circle
Your body pivots over your front foot, and you bring your rear foot forwards to take the next stride
In a walking gait, your body is in circular motion as you pivot your forward foot
Since she is in circular motion acceleration is pointing downwards so that means that Fn has to be less than weight in order for there to be a net force
Your body tries to “lift off” as it pivots over your foot, decreasing in normal force exerted on you by the ground
Normal force becomes smaller as you walk faster, but Fn cannot be less than zero
This means that maximum possible walking speed vmax occurs when Fn is equal to zero

Apparent Forces in Circular Motion
In a carnival ride, people feel “stuck” to the inside wall
Riders feel that they are being pushed outward, into the wall, why is that?
Centrifugal Force ?
When you are in a car and you make a sharp turn, you feel like you're being thrown by some mysterious force
This is because your body is trying to continue moving in a straight line - obeying newton's first law
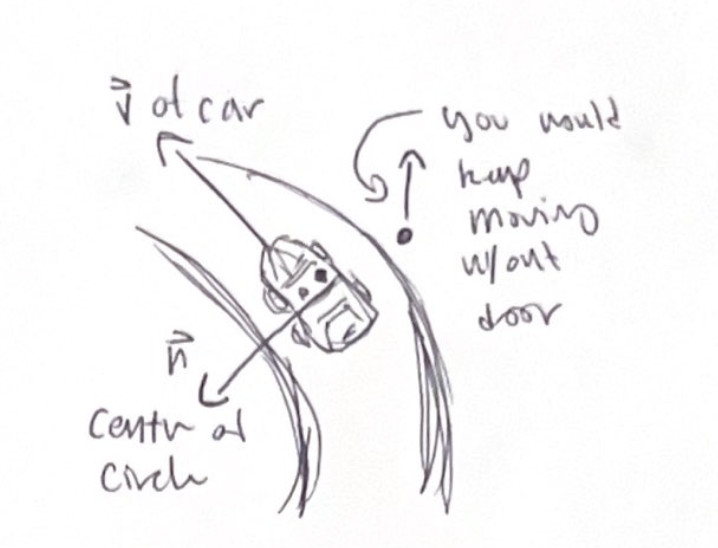
Without the door you’d keep moving straight ahead
The door provides the center-directed force that makes you move in a circle
Door starts to turn in towards you and in turn runs into you!You feel the force of the door pushing inward toward the center of the curve, causing you to turn the corner
Not “thrown” into the door, the door ran into you
This “force” that seems to push an object ot the center of a circle is called a centrifugal force
Not an actual force, what you feel is your body trying to move ahead in a straight line, trying to take you away from traveling in a circle
Only real forces are the forces that appear on a free-body diagram, the forces pushing inward towards the center
A centrifugal force will never appear on a free-body diagram and never be included in newtons laws
Going back to the carnival ride, the riders feel as if they’re being pushed outwards because of our natural tendencies to move in a straight line being resisted by the ride
Feelings aren’t forces ☹ only actual forces is the contact force of the ride pushing inwards
Apparent weight in circular motion
If you swing a bucket of water over your head, when you swing it quickly the water stays in, if you swing it too slowly the water falls out
your sensation of weight changes as you go over the crescents and through dips
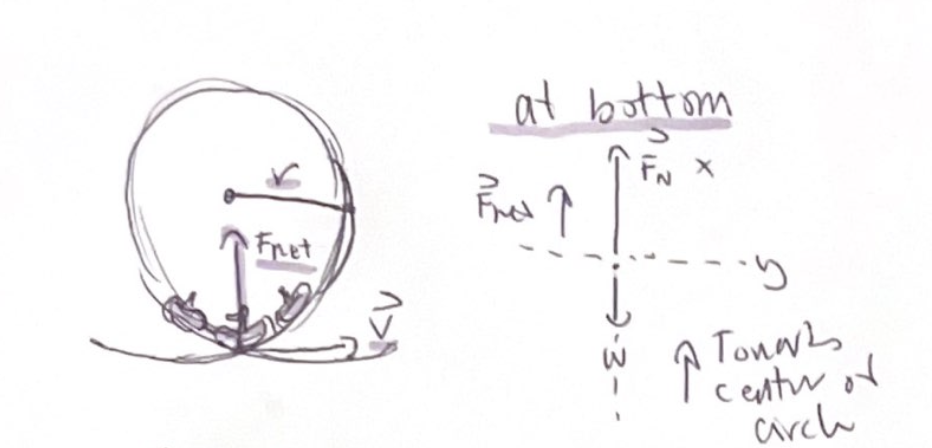
Reminder when drawing FBD, you should define x-axis as always points towards the center of the circle
Examining a rollercoaster at bottom, the only forces acting on her are weight and Fn, remember you don’t feel your weight, you feel your apparent weight, the magnitude of the contact force
Based on circular motion we can say:
She is moving in a circle, so there must be a fnet pointing towards the center of the circle, which is currently above her head, to provide centripetal acceleration
Fnet points upward so Fn is greater than w
Her apparent weight is equal to applied force, wapp = Fn
So her apparent weight is greater than her true weight (wapp > w), This feeling “heavier” at the bottom of the circle
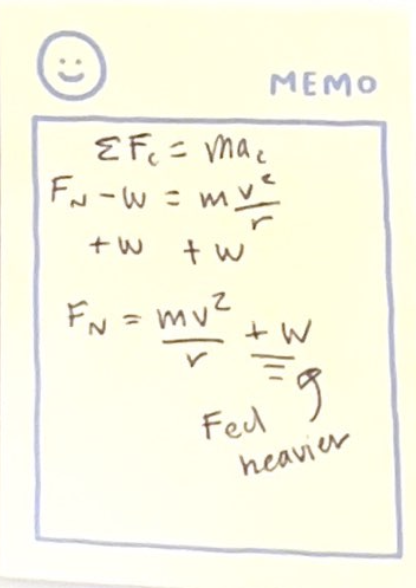
apparent weight at bottom is greater than her true weight
Now looking at the top of the roller coaster
\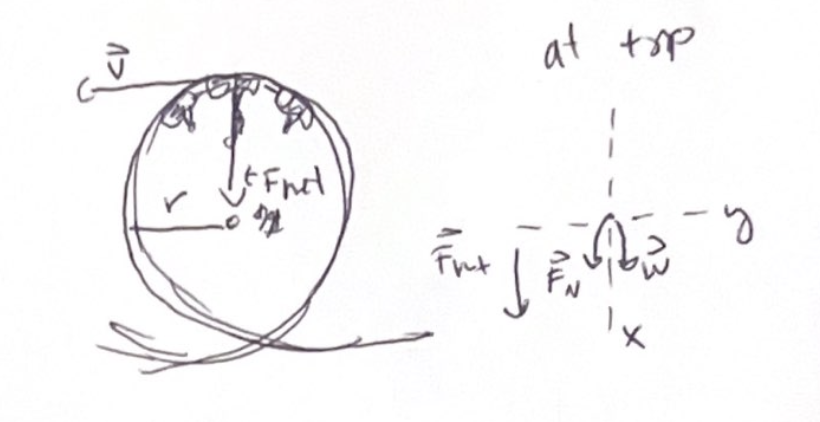
Before Fn pushed up towards the center of the circle at the bottom, now it pushes down when she is at the top and the seat is above her
Passenger is still moving in a circle so there must be a net force downwards towards the center of the circle, providing her centripetal acceleration

If velocity is large enough, her apparent weight can exceed her true weight
Lets look at the cart of the rollercoaster, what happens when the cart goes slower?
Looking at Fn = mv²/r - w, as velocity decreases, a point comes where mv²/r has the same value as weight (Fn = w - w), making Fn equal to zero
At this point the seat is not pushing the passenger at all !
This is why height restrictions on roller coasters are necessary, without proper height, it could lead to a situation where the normal force isn’t sufficient to keep the child in place, resulting in a situation where Fn = zero and putting the child at risk of falling ☹
On a rollercoaster, you are able to complete the circle because weight force provides sufficient centripetal acceleration
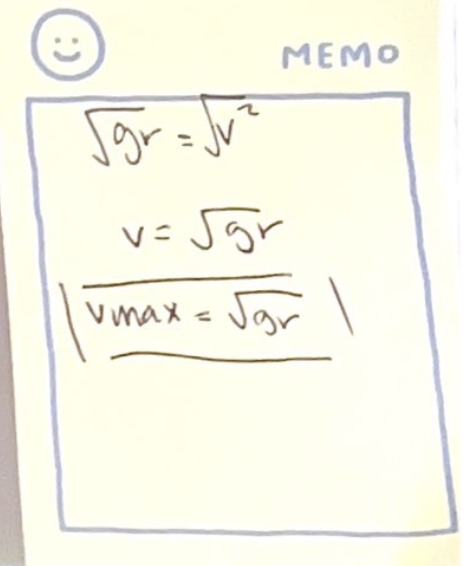
The speed for which Fn = 0 is called the critical speed or vc
For Fn to be zero we must have mv²/r equal to w, so critical speed is:
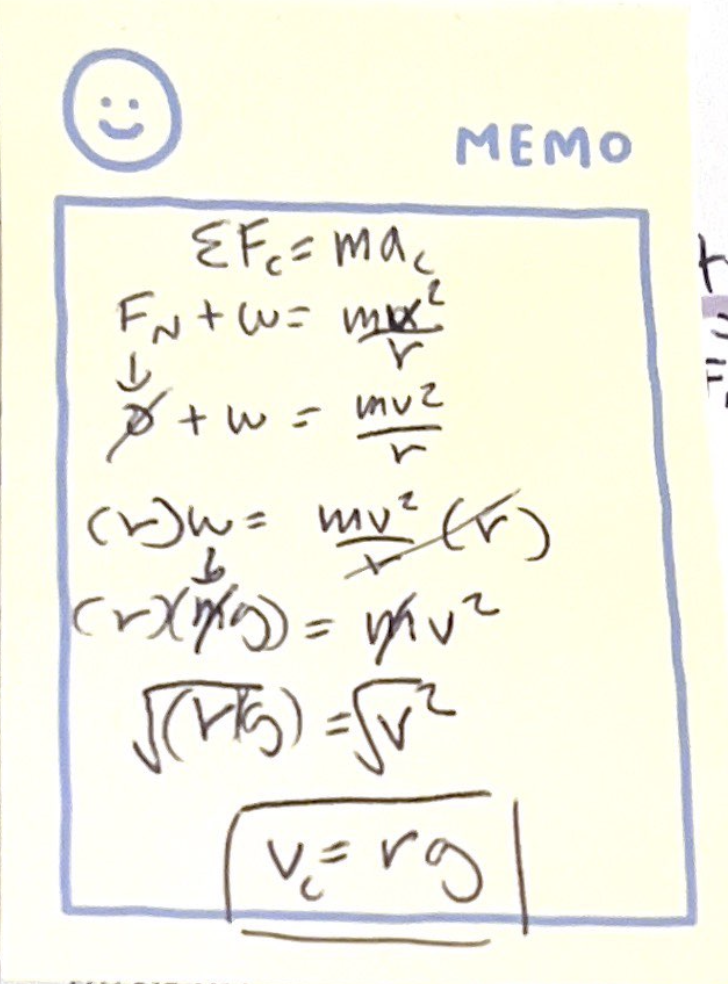
What would happen if the speed was slower than the critical speed?
v = √rg would give a negative value for Fn if velocity is smaller than critical speed
This is physically impossible since the seat can push against the passenger but it can't pull her, remember that Fn can only be a push, not a pull
This means that the slowest possible speed is the speed for which Fn = 0 at the top
Critical speed is the slowest speed at which the cart can complete the circle
If Fn becomes negative then the force goes up on a free body diagram
If velocity is smaller than critical speed, the passenger cannot turn the final loop, instead will fall from the cart as a projectile boom !
Reason as to why we wear straps on a rollercoaster
Water stays in a bucket swinging around your head for the same reason
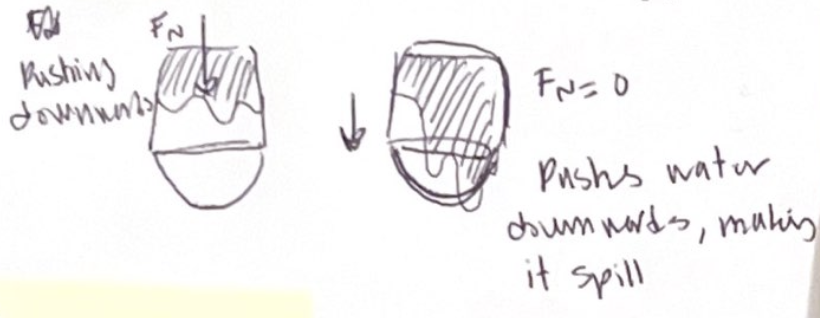
Bottom of bucket pushes against the water to provide the inward force that causes circular motion
If you swing bucket too slowly, the force of the bucket on the water drops to zero
Water leaves the bucket and falls onto your head !