1. Sensitivity Analysis
Page 1: Introduction to What-if Analysis
Topic: What-if Analysis (Sensitivity Analysis) for Linear Programming
Instructor: Rim Jaber
Course: ADM2302
Page 2: Understanding the Assumptions
Assumption: Model parameters are known with certainty.
Reality: Model parameters are estimates and can change.
Example: Referring to the RMC Problem for context.
Page 3: The RMC Example
Company Overview: RMC, Inc. produces chemical-based products using three raw materials for two products.
Material Usage per Product:
Fuel Additive:
Material 1: 2/5 tons per ton
Material 2: 0 tons
Material 3: 3/5 tons per ton
Solvent Base:
Material 1: 1/2 tons per ton
Material 2: 1/5 tons per ton
Material 3: 3/10 tons per ton
Available Material for Production:
Material 1: 20 tons
Material 2: 5 tons
Material 3: 21 tons
Profit Contribution:
Fuel Additive Profit: $40/ton
Solvent Base Profit: $30/ton
Goal: Determine tons of each product to maximize total profit.

Solution:


it will remain the same because between $40 and $50 there is a change of 10 which is allowable because it is within the allowable increase of 20 (0.4X1+0.5X2<=20)



The new optimal solution would now be (35,0) because the profit contribution of solvent based has dropped (Q2)

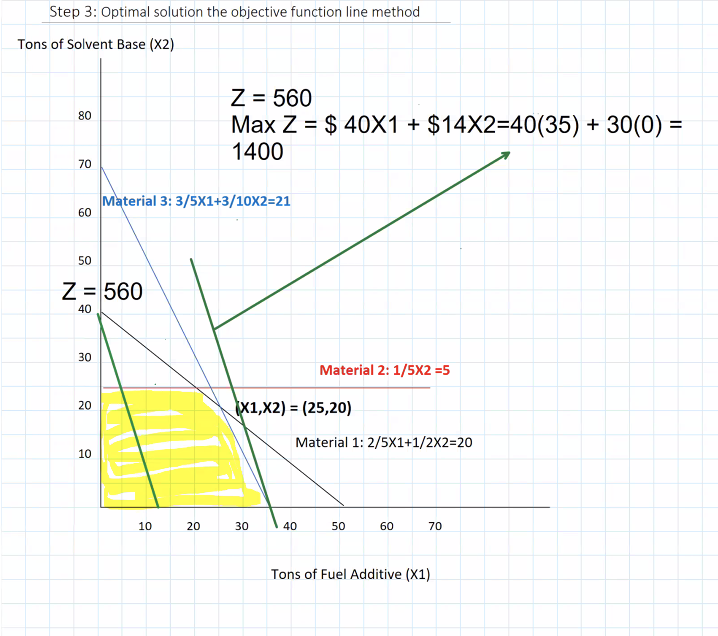




if we change binding constraints then the corner points would change




Page 4: Formulation of RMC Problem
Objective Function:
Maximize Z = $40 * x1 + $30 * x2
Constraints:
(2/5)x1 + (1/2)x2 ≤ 20 (Material 1)
(1/5)x2 ≤ 5 (Material 2)
(3/5)x1 + (3/10)x2 ≤ 21 (Material 3)
x1 ≥ 0, x2 ≥ 0
Variables:
x1: tons of fuel additive
x2: tons of solvent base
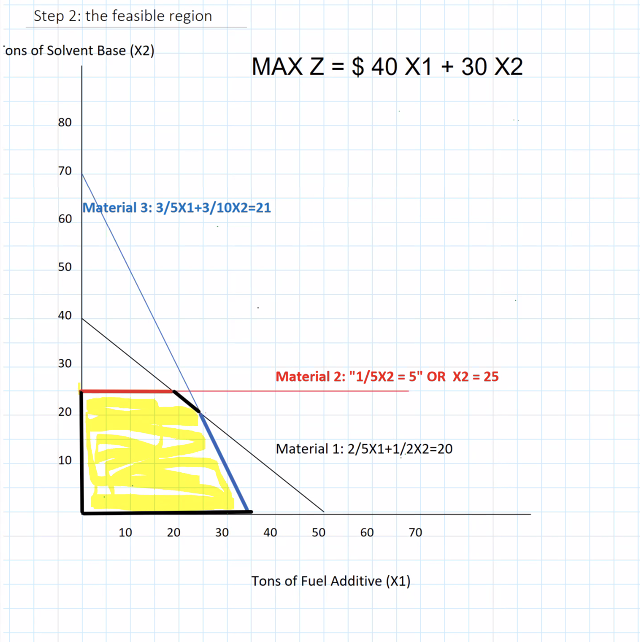
Page 5: The Feasible Region
Graph:
x1 on horizontal axis
x2 on vertical axis
Constraints represented as lines:
2/5x1 + 1/2x2 = 20
1/5x2 = 5
3/5x1 + 3/10x2 = 21
Page 6: Finding Optimal Solution
Corner Points Identified:
(25, 20), (18.75, 25), (0, 25), (0, 0), (35, 0)
Optimal Solution using Corner Point Method:
Calculation of Z for each point
Page 7: Optimal Solution Analysis
Calculated Values of Z:
Z(25, 20) = $750
Z(18.75, 25) = $1500
Z(0, 25) = $0
Z(35, 0) = $1400
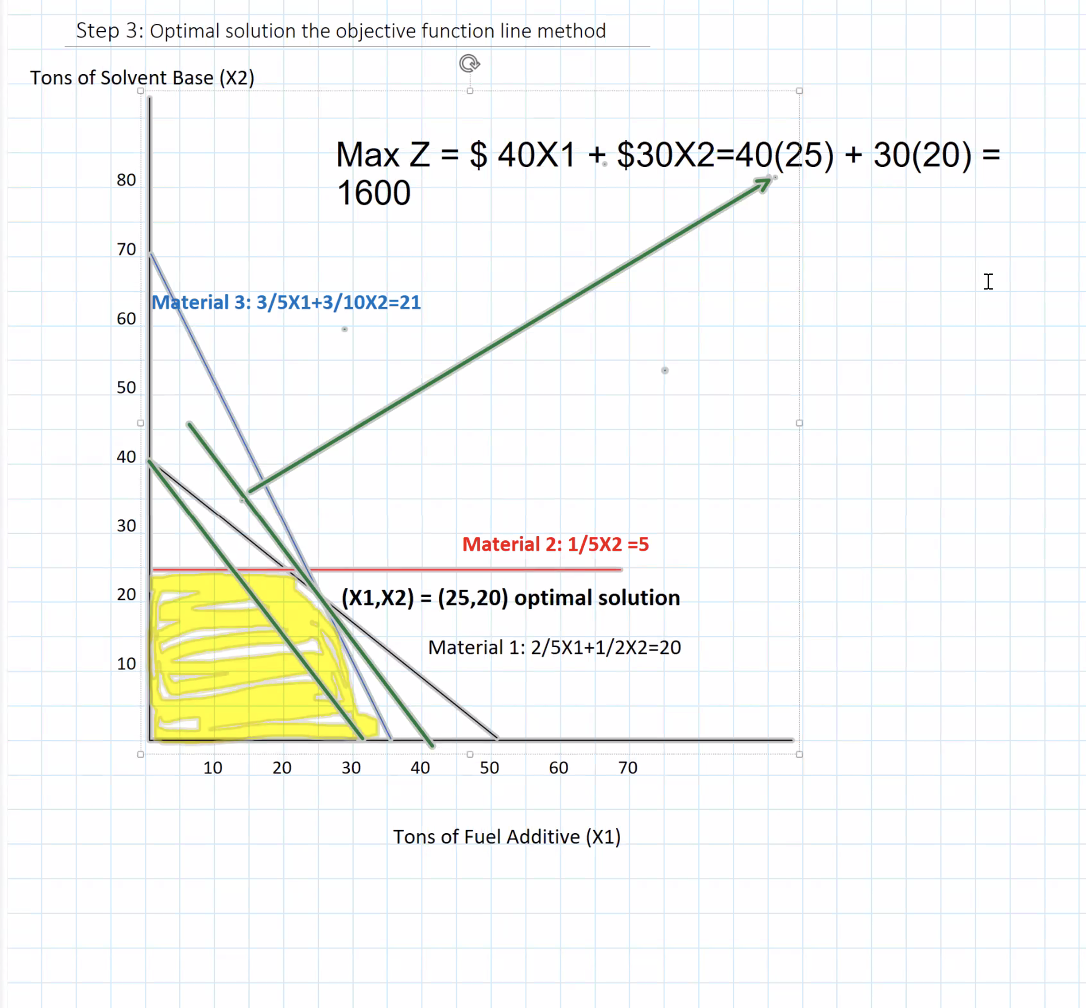
Z(25, 20) = $1600
Optimal Solution Found: at (25, 20)
Page 8: Objective Function Line Method
Maximum Isoprofit Line:
Represented as Z = $1600
Optimal Solution Point identified at (25, 20)
Page 9: Developing a Spreadsheet Model
Spreadsheet Reference: RMC_Problem.xlsx
Formula Examples:
fx =SUMPRODUCT(B5:C5,$B$3:$C$3)
Variables in Spreadsheet:
D5: Solution
D8 to D10: Material constraints analyzed
Page 10: Objective Cell Summary
Profit Totals:
Original: $0
Final Value: $1,600
Variable Cells:
x1 (Fuel Additive): 0 to 25
x2 (Solvent Base): 0 to 20
Binding Constraints Identified:
Material 1: Binding
Material 2: Not Binding
Material 3: Binding
Page 11: Sensitivity Report Overview
Variable Cells Summary:
Final Value, Reduced Cost, Objective Coefficient
Allowable increase/decrease for x1 (fuel additive) and x2 (solvent base)
Constraints Analysis: Shadow price evaluations
Page 12: What-if Analysis Explanation
Definition and Purpose: Sensitivity analysis questions the effect of parameter changes on optimal solutions
Page 13: Outline of Analysis Topics
Changes in Objective Functions Coefficients
Changes in Right-Hand Sides (RHS) Values
Shadow Prices
Range of Feasibility
Simultaneous Changes
Reduced Costs
Pricing out New Variables
Page 14: Changes in Objective Functions Coefficients
Understanding Coefficients (both are found from the objective function):
c1 for x1 (c1=40)
c2 for x2 (c2=30)
Goal of Sensitivity Analysis:
Determine range of c that keeps the current solution optimal.
Page 15: Graphical Analysis of Coefficient Changes
Implication: Objective function coefficients do not affect feasible region size (the only thing that happens when changing the coefficients is a change in the slope of the objective function)
Range of Optimality:
x1: 24 ≤ c1 ≤ 60
x2: 20 ≤ c2 ≤ 50
Page 16: Impact on Value of Z
Zero value decision variable: Non-use does not change Z
Non-zero value decision variable: Affects Z positively or negatively
Page 17: Unit Profit Estimates
Question and Answer: What if profit estimates are inaccurate? A wide range of values ensures likely optimal solution integrity
Page 18: Changes in RHS Values
Impact of Changes in Constraints: Affect feasible region and optimal solution value
RHS Values: e.g., Q1 = 20, Q2 = 5, Q3 = 21
Page 19: Optimal Solution Assessment
Optimal Points: Evaluating through graphical representation
Page 20: Shadow Price Definition and Calculation
Understanding Shadow Prices:
Increase profits per additional resource unit
How to Determine: Increase RHS in spreadsheet, solve anew
Page 21: Shadow Prices in Context
Definitions:
Marginal profit & max price willing for resources
Profit decreases by 1 unit reduction
Page 22: Purpose of RHS Value Analysis
Objective: Examine small changes in RHS and their impact
Page 23: Range of Feasibility with RHS
Value Ranges:
Q1: 14 ≤ Q1 ≤ 21.5
Q2: 4 ≤ Q2
Q3: 18.75 ≤ Q3 ≤ 30
Page 24: Changes Analysis of Binding vs Non-Binding Constraints
Impact: Changes in binding constraints change optimal solution; non-binding do not affect profit unless within range
Page 25: Simultaneous Changes in Coefficients
Purpose: Determine potential changes in optimal solution under multiple coefficient changes simultaneously
Page 26: 100 Percent Rule for Objective Function Coefficients
Application: Total allowable changes must not exceed 100% to maintain optimal solution
Page 27: Example of 100 Percent Rule
Illustration: c1 and c2 adjustments confirmed the stability of the current optimal solution
Page 28: Example of Exceeding 100 Percent Rule
Outcome: Re-evaluate optimal solution needs resolving due to rule breach
Page 29: 100 Percent Rule for RHS
Sum of changes: Assess RHS adjustments under feasibility ranges
Page 30: Class Discussion Summary
Topic Validity and Examples discussed
Page 31: Reduced Cost Interpretation
Concept: Explanation of reduced costs for unused activities; relevant for analysis and strategy
Page 32: Indicator of Multiple Optimal Solutions
Criteria: Identifying zero optimal values and implications for solution stability
Page 33: Evaluating New Variables Introduction
Sensitivity Report uses: Assessing the impact of variable changes on current production
Page 34: Proposing New Products for Production
Example Evaluation of Ultra Base with material consumption and profit contribution
Page 35: Opportunity Cost Analysis
Checking shadow price validity; guiding production decisions based on opportunity cost assessment
Page 36: Additional Discussions from Class
Summary of solutions discussed in-depth during sessions
Page 37: Summary of Sensitivity Reports (Objective Function Coefficients)
Final Values: Review usage and changes in objective coefficients
Allowable Changes: Define operational ranges for coefficients
Page 38: Summary of Sensitivity Reports (Right-Hand-Sides)
Final Values and Shadow Prices: Implications for resource adjustments and their operational impact.