What to include when solving problems

• Reference frame

• Picture

• List given variables

• List what you need to find

• Pure equations (no substitutions)

• Step by step solutions

• Units

• Show unit cancelations

New Variables

N = Newton, J = joule, W = watt

Chapter 4: Forces and Newton’s Laws of Motion

Newton’s Three Laws of Motion

• Newton’s 1st Law - An object in motion stays in motion or an object at rest stays at rest unless an external force is applied.

• Newton’s 2nd Law - The net force on an object is equal to the object's mass multiplied by its acceleration: F=ma (F=ma_{x} or F=ma_{y})

• Newton’s 3rd Law - For action action there is an equal and opposite reaction.

Forces

• Force (N) - a push or pull required to change the state of motion of an object

  • SI unit for force = Newton (N)

  • Newton = \dfrac{kg\cdot m}{s^{2}}

  • \dfrac{N}{kg}=\dfrac{m}{s^{2}}

• Net force - vector sum of all forces acting on an object.

  • If no net force acts on an object, the object’s velocity can not change and the object can not accelerate.

• Inertia - The natural tendency of an object to remain at rest or in motion at a constant speed along a straight line. Resistance to a change in velocity.

  • Inertial reference frame - non-accelerating frames of reference.

  • All accelerating reference reference frames are non-inertial.

Free Body Diagrams

• Free body diagrams - represents the object and the forces that act on it, object is usually represented by a dot.

Weight

• Weight: W=mg

• Always acts downwards towards center of body.

Newton’s Law of Universal Gravitation

• Every particle in the universe exerts an attractive force on every other particle.

• For two particles, which have masses m₁ and m₂ and are separated by a distance r, the force that the particles, and has a magnitude given by:

  • F=G\dfrac{m_{1}m_{2}}{r^{2}}

  • Universal gravitational constant: G = 6.67259× 10^-11 \dfrac{Nm^{2}}{kg^{2}}

• Inverse square law: The inverse square law states that a physical quantity decreases as the square of the distance ( r ) from a source increases.

• Mass of the earth: W=G\dfrac{M_{E}m}{r^{2}}

Normal Force

• Normal force - the component of a contact force that is perpendicular to the surface that an object contacts, magnitude of the normal force indicates how hard the two objects press against each other.

• If an object is resting on a surface, there are no vertical forces acting on them. The magnitudes of these two forces are equal.

Apparent Weight

• Apparent weight of an object is the reading of a scale.

  • F_{N}=mg+ma

Static and Kinetic Friction

• Friction is always the opposite direction of motion and is parallel to the surface.

• Static friction - frictional force resists force that is applied to an object, object remains at rest until the force of static friction is overcome.

• Maximum static friction - the force just before breakaway (right before object starts moving).

  • f_{s}^{MAX}=\mu_s \cdot F_{N}

• Kinetic friction - force that acted between moving surfaces.

  • f_{\text{k}} = \mu_k \cdot F_{N}

  • 0\leq \mu _{k} is the coefficient of kinetic friction.

Three Main Characteristics of Kinetic Frictional Force

1. It is independent of the apparent area of contact between the surfaces

2. It is independent of the speed of the sliding motion, if the speed is small.

3. The magnitude of the kinetic frictional force is proportional to the magnitude of the normal force.

Tension

• Cables and ropes transmit forces through tension.

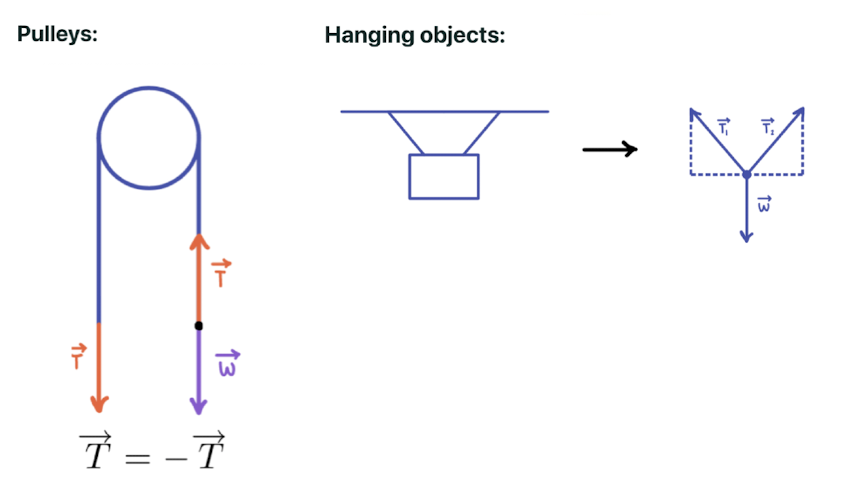
Equilibrium and Nonequilibrium

• Equilibrium - the lack of change in the velocity of an object (the object is not accelerating).

  • ZERO ACCELERATION (\sum F_{x}=0 or \sum F_{y}=0)

  • Velocity will not change.

• Accelerating object = NOT in equilibrium. (\sum F_{x}=ma_{x} or \sum F_{y}=ma_{y})

  • When \Sigma F\neq 0 , the net F will make the system accelerate, so its velocity WILL change. It will speed up, slow down, or stop.

• Newton’s laws apply to objects whether or not they are in equilibrium.

• The forces acting on an object in equilibrium must balance.

• An object can be moving and still be in equilibrium if there is no acceleration.

• Equilibrium

  • Parked car, objects moving at constant speed and not changing directions.

• Non-Equilibrium

  • A car starting from a stop and moving straight through an intersection.

    • Accelerating.

  • A car making a right turn at constant speed.

    • There is a change in direction.

Chapter 5: Uniform Circular Motion

• Uniform circular motion - the motion of an object traveling at a constant speed on a circular path (constant speed = uniform).

  • Equation for circular velocity: v_{c}=\dfrac{2\pi r}{T}

  • Speed (magnitude) is constant, direction is not constant, so velocity is not constant.

• Revolution - a singular circular orbit of one body around a point.

• Period - time it takes an object to travel once around a circle (to make one revolution).

  • Period (T)=\dfrac{1}{frequency}

  • Frequency is the number of revolutions.

• Circumference of a circle: 2\pi r (in meters)

Centripetal Acceleration

• In uniform circular motion, speed is constant, but direction of the velocity vector is not constant.

• Centripetal acceleration - directed towards the center of the circle; the same direction as the change is velocity

  • a_{c}=\dfrac{v^{2}}{r}

• Spinning an object in circular motion:

  • When the object is released, it will move along a straight path (Newton’s 1st law).

  • Once the object is released, there is no net force acting on it.

Centripetal Force

• Centripetal force - the net force required to produce centripetal acceleration to keep an object moving in a circular path (newton’s second law).

• Direction: ALWAYS towards the center of the circle, continually changes direction as the object moves.

• There are two ways to write this equation:

  • F_{c}=ma_{c} or F_{c}=\dfrac{mv^{2}}{r}

    • The second equation inserts the centripetal acceleration equation.

Satellites in Circular Motion

• There is only one speed and period that a satellite can have if the satellite is to remain in an orbit with a fixed radius. When something is in orbit, gravity is the centripetal force.

• The speed of a satellite: v=\sqrt{\dfrac{GM_{E}}{r}}

• The period of a satellite:T=\dfrac{2\pi r^{\dfrac{3}{2}}}{\sqrt{GM_{E}}}

• Universal gravitation constant: G = 6.67\times 10^{-11}\dfrac{Nm^{2}}{kg^{2}}

Apparent Weightlessness and Artificial Gravity

• Apparent Weightlessness - occurs when an object is falling freely under the influence of gravity, giving the sensation of weightlessness.

• Artificial Gravity - a concept of simulating gravity through centrifugal force or acceleration to create a gravitational effect in space or other environments.

Chapter 6: Work and Energy

• Work is a force applied over a distance (force x displacement)

  • W=Fs

  • W=F\cos \theta s

• The Joule: 1N\cdot m=1joule\left( J\right)

• When a force is PARALLEL to the displacement, the work by the force is POSITIVE.

• When a force is OPPOSITE to the displacement, the work done by the force is NEGATIVE.

• When the force is PERPENDICULAR to the displacement, the work done by the force is ZERO.

Work Energy Theorem

• Kinetic energy (KE) of an object with mass m and speed v. Energy in motion.

  • KE=\dfrac{1}{2}mv^{2}

  • KE will always be positive because mass can not be negative and v² is always positive.

• Work-energy theorem - the net work done by the forces on an object equals the change in its kinetic energy. When a net external force does work on an object, the kinetic energy of the object changes by the amount of work done on it:

  • W=KE_{f}-KE_{0}

Gravitational Potential Energy

• Potential energy (PE) - stored energy

  • PE=mgh

• Gravitational potential energy - the energy that an object of mass m has by virtue of its position relative to the surface of the earth.

  • W_{gravity}=mg\left(h_{0}-h_{f}\right)

• Potential and Kinetic energy

  • When your PE is at maximum, your KE is zero.

  • When your PE is zero, your KE is at maximum.

Conservative vs Nonconservative Forces

• The gravitational force is called a conservative force and occurs when:

  • The work it does on a moving object is independent of the path between the object’s initial and final positions.

  • It does no work on an object moving around a closed path, starting and finishing at the same point.

• The total mechanical energy of the system remains constant if only conservative forces are acting on it.

• When a path has the same starting and ending point, it is called a closed path.

  • For a closed path, the work done by gravity will equal zero joules.

  • W_gravity = 0 J for a closed path.

Working Together

• When conservative forces and nonconservative forces act simultaneously on an object, we can write work as:

  • W=W_{c}+W_{nc}

Conservative vs Nonconservative Table

• The gravitational force is called a conservative force and occurs when:

  • The work it does on a moving object is independent of the path between the object’s initial and final positions.

  • It does no work on an object moving around a closed path, starting and finishing at the same point.

• The total mechanical energy (kinetic energy + potential energy) of the system remains constant if only conservative forces are acting on it.

• Closed path - when a path has the same starting and ending point

  • Work done by gravity => W_gravity = 0 J for a closed path.

Working Together

• When conservative forces and nonconservative forces act simultaneously on an object, we can write work as: W=W_{c}+W_{nc}

Conservative vs Nonconservative Table

The Conservation of Mechanical Energy

• If the net work on an object by nonconservative forces is zero, then its energy does not change.

• Conservation of energy: E_{f}=E_{0} OR \dfrac{1}{2}mv_{f}^{2}+mgh_{f}=\dfrac{1}{2}mv_{0}^{2}+mgh_{0}

• Total mechanical energy: E=KE+PE

  • The total mechanical energy of an object remains constant as the object moves, provided that the net work done by external nonconservative forces is zero.

Nonconservative Forces and the Work-Energy Theorem

• Most moving objects experience nonconservative forces, such as friction, air resistance, and propulsive forces, and the work W_nc done by the net external nonconservative force is not zero. In these situations, the difference between the final and initial total mechanical energies is equal W_nc. Can be written in two ways:

  • W_{nc}=E_{f}-E_{0}

  • W_{nc}=\left( mgh_{f}+\dfrac{1}{2}mv_{f}^{2}\right) -\left( mgh_{0}+\dfrac{1}{2}mv_{0}^{2}\right)

Power

• Average power (\overline{P}) is the time rate at which work is done.

  • \overline{P}=\dfrac{W}{t}

    • W is also equal Fs, s/t is equal to \overline{v}, can be written as\overline{P}=F\overline{v}

  • SI Unit: watt (W) aka joule/s

• The work–energy theorem relates the work done by a net external force to the change in the energy of the object.

  • We can also define average power as the rate at which the energy is changing, or as the change in energy/time during which the change occurs.

• 1 horsepower = 550ft\cdot lbs/\sec = 745.7 watts

The Principle of Conservation of Energy

• Energy can neither be created nor destroyed, but can only be converted from one form to another.

Extra

Average speed - how fast something travels over a certain distance: distance/elapsed time

Average velocity - how fast an object’s position changes over time: \overrightarrow{\overline{v}}=\dfrac{\Delta \overrightarrow{x}}{\Delta t}

Average acceleration - rate at which an object’s velocity changes over a period of time: \overrightarrow{\overline{a}}=\dfrac{\Delta \overrightarrow{v}}{\Delta t}

Speed vs. Velocity vs. Acceleration

1. Speed: How fast you're going, like on a speedometer. It's just a number, no direction.

2. Velocity: Speed with direction. It's how fast you're going and in which direction.

3. Acceleration: Changes in velocity. Speeding up, slowing down, or changing direction.

Velocity and Acceleration

• Velocity, no acceleration = constant velocity

• Velocity with acceleration = speeds up as it moves

• When acceleration and velocity have opposite directions, the object slows down and decelerates.

Kinematic Equations

v=v_{0}+at

x=\dfrac{1}{2}\left( v+v_{0}\right) t

x=v_{0}t+\dfrac{1}{2}at^{2}

v^{2}=v_{0}^{2}+2ax