Rotational dynamics is a branch of physics that studies how and why objects rotate. It examines the forces, torques, and energy involved in rotational motion. By understanding concepts such as torque, angular acceleration, moment of inertia, and angular momentum, we can analyze the motion of objects ranging from spinning tops to orbiting celestial bodies. Below is a comprehensive breakdown of the core concepts, equations, and their significance.

1. Torque (τ)

• Formula:

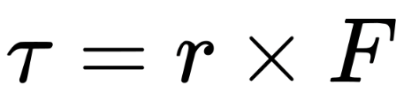
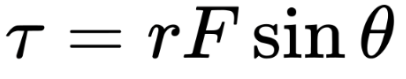
• Definition:
  Torque is the rotational counterpart of force. It measures how effectively a force causes an object to rotate about a pivot or axis.

Key Points:

• Right-Hand Rule: Determines the direction of torque (clockwise or counterclockwise).

• Dependencies:

  • Force (F): A larger force generates a larger torque.

  • Lever Arm (r): The perpendicular distance from the axis of rotation to the line of action of the force.

• Angle (θ): Torque is maximized when the force is perpendicular to the lever arm (θ=90∘).

2. Angular Acceleration (α)

• Formula:

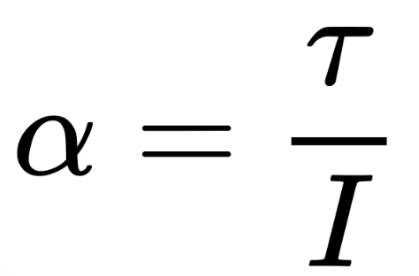
• Definition:
  Angular acceleration is the rate at which an object’s rotational speed changes. It describes how quickly an object speeds up or slows down in rotational motion.

Key Points:

• Proportional to Torque (τ): Applying more torque increases angular acceleration.

• Inversely Proportional to Moment of Inertia (I): Heavier or larger objects with more mass distributed away from the axis resist angular acceleration.

• Example: A lightweight wheel accelerates faster than a heavier one for the same applied torque.

3. Moment of Inertia (I)

• Formula:

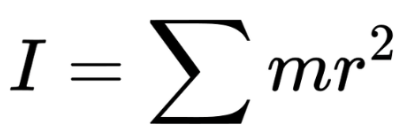
• Definition:
  The moment of inertia is a measure of an object’s resistance to changes in its rotational motion. It depends on both the mass of the object and how that mass is distributed relative to the axis of rotation.

Key Points:

• Objects with mass farther from the axis (e.g., hollow cylinders) have a higher III, making them harder to spin or stop spinning.

Examples of III for common shapes:

• Solid disk about central axis: 

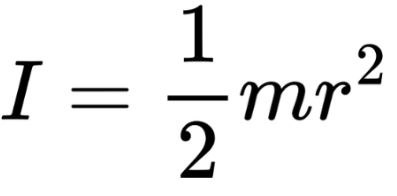
• Hollow Cylinder:

  

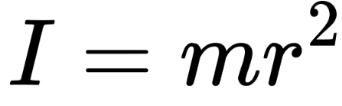
• Solid sphere about central axis: 

  

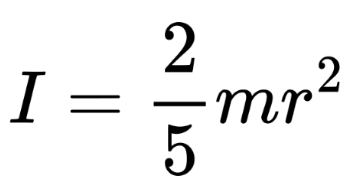
4. Angular Momentum (L)

• Formula:

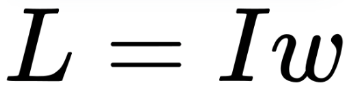
• Definition:
  Angular momentum is a conserved quantity that represents the amount of rotational motion an object has.

Key Points:

• Conservation of angular momentum states that if no external torque acts on a system, the total angular momentum remains constant: 

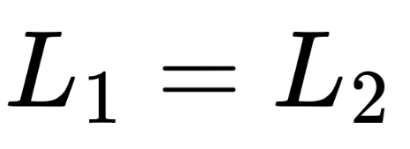
Applications:

• A figure skater spins faster by pulling in their arms (reducing III, increasing ω\omegaω).

• Rotational dynamics in astronomy, like spinning neutron stars (pulsars).

5. Rotational Kinetic Energy (KE)

• Formula:

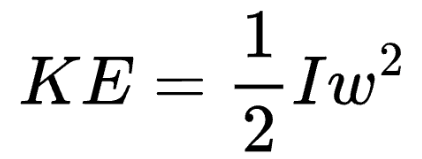
• Definition:
  Rotational kinetic energy is the energy an object possesses due to its rotation. It is similar to translational kinetic energy but involves III and angular velocity ω\omegaω.

Key Points:

• Objects in combined motion (rotational and translational) have both rotational and translational kinetic energy.

Example: A rolling cylinder’s total kinetic energy includes both forms: 

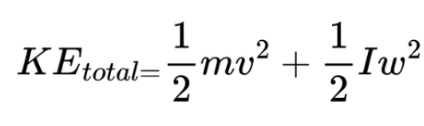
6. Work-Energy Theorem for Rotation

• Formula:

  

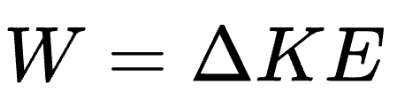
• Definition:

• The work done by torque on a rotating object results in a change in its rotational kinetic energy.

Key Points:

• Analogous to the linear work-energy theorem: 

  

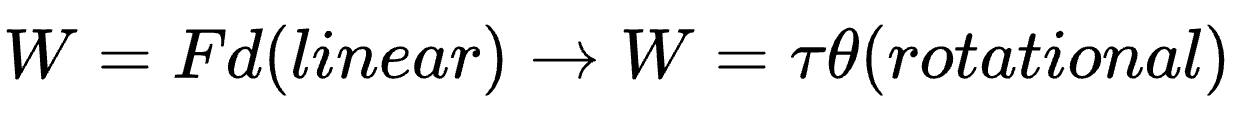
7. Power in Rotational Motion (P)

• Formula:

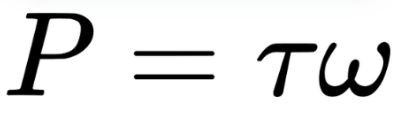
• Definition:
  Power in rotational systems measures the rate at which work is done or energy is transferred in a rotating object.

Key Points:

• Important in engines, turbines, and other systems where rotation drives power transfer.

8. Angular Velocity (ω)

• Formula:

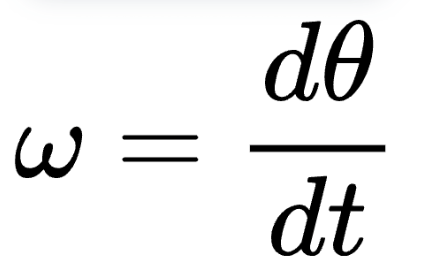
• Definition:
  Angular velocity describes how fast an object is rotating, measured in radians per second.

• Key Points:

  • Positive ω omega: Counterclockwise rotation.

  • Negative ω omega: Clockwise rotation.

9. Angular Displacement (θ)

• Formula:

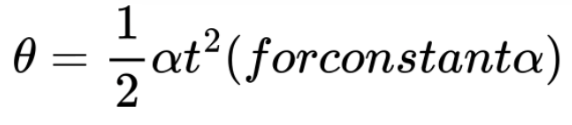
• Definition:
  Angular displacement is the angle an object rotates through over time.

Key Points:

• Useful in analyzing rotational motion under constant angular acceleration.

• Parallel to linear displacement formulas in kinematics.

Applications and Real-Life Examples

• Energy Conservation:

  • Wind turbines convert rotational energy into electrical energy.

  • Flywheels store rotational kinetic energy for later use.

• Sports and Movement:

  • A diver or gymnast tucks their body to spin faster (reducing III, increasing ω\omegaω).

• Astronomy:

  • Conservation of angular momentum explains why stars spin faster as they collapse.

• Engineering:

  • Gears and pulleys use torque and angular velocity to transfer mechanical energy efficiently.