PY 131 Chapter 35: Special Theory of Relativity

Special Relativity

• In the late 1800s, there was still some confusion about the nature of light.

• The general consensus at the time was that light was the traveling vibrations of a medium called the aether.

• Several experiments tried to detect Earth’s motion with respect to the aether.

• For example:

  • measure the speed of light in moving water and still water,
  • measure the speed of light at different times of the year when the Earth is at different points on its orbit
  • measure the speed of light traveling in different directions

• A common denominator of all these experiments was consideration of what is happening in different frames of reference.

• A reference frame is a set of coordinates and a clock.

  

• If something occurs, an ‘event’, then we can assign a set of spatial coordinates and a time to the event.

• The assignments will be different for each frame of reference.

• In the case of the aether experiments, it was thought that if light travels at c in the aether and the experiment is moving with respect to the aether, then the speed of light as measured by the experiment will not be c, it will be larger or smaller.

  • the situation is similar to sending a sound wave between two moving aeroplanes which are a fixed distance apart with one behind the other

• However, none of the experiments ever detected the motion of the Earth with respect to the aether.

• Furthermore, any modification of the aether to explain the null results led to predictions that were not compatible with other experiments.

• This (and other considerations) led Einstein to reject the existence of the aether.

The Postulates of Special Relativity

• Einstein based his new theory on two postulates:

The laws of nature are the same in all uniformly moving frames of reference

• (BTW Newton also said something similar.)

The speed of light in a vacuum is the same for all observers, regardless of the motion of the light source or observer.

• The consequences for our understanding of space and time are greatly affected by these postulates.
• Two events which are simultaneous in one frame of reference may not be simultaneous in another.
• The time measured between events in one frame of reference may be different from the time measured between the same events in another.
• The distance between two points in space measured in one frame of reference may be different from the distance measured between the same two points in another.
• The mass of an object measured in one frame of reference may be different from the mass measured in another.

Simultaneity

• Consider a train car with an observer inside and a light source at its center. At a chosen instant, the light is switched on.

• At either end of the car is a special clock that is turned on when the light reaches it.

  

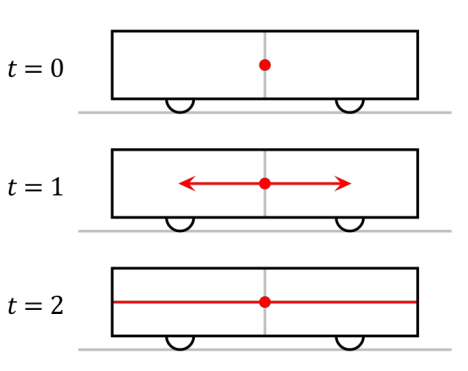
• According to the observer in this car, the light hits both clocks simultaneously and both show the exact same time.

• Now consider an observer watching the train car move past with some speed.

• This observer also sees the light switch on but this observer sees the light hit the clock at the back before it hits the one at the front.

  

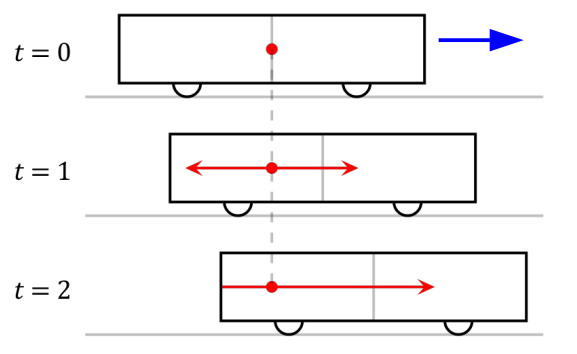
• In this reference frame the two clocks are not synchronized.

  • the clock at the rear will show more time has elapsed since it was hit than the one at the front.

• Now consider an observer in second train car which is traveling faster than the first, in the same direction.

• The first car appears to be traveling backwards to this observer

  

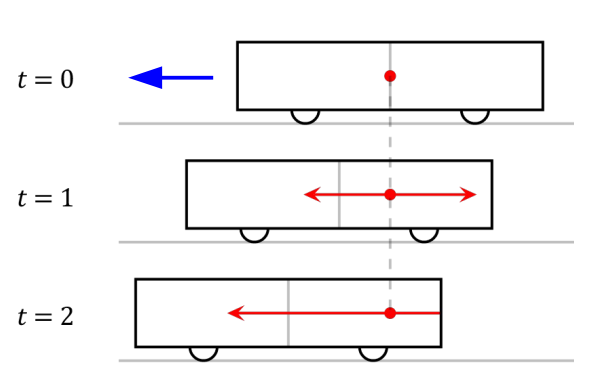
• According to this observer, the light in the first car hits the clock at the front before it hits the one at the back.

• According to this observer, the clock at the front of the first car shows more time has elapsed since it was hit that the one at the rear.

• Who is right? Do the clocks show the same time or different times, and if the times are different, which clock shows more time has elapsed since it was started?

  • They are all correct: what one observer sees in their frame of reference is not trivially related to what the others see.
  • The relationships are more complicated because everyone must observe the speed of light to be the same and independent of their own motion.

• Two events – the light starting the clocks – are not always simultaneous if they occur at different locations.

• The only way two events which are simultaneous in one frame of reference can be simultaneous in another is if they occur at the same place.

\
Consider two events A and B.

• If the two events do not occur at the same place then it is possible to find two frames of reference where in one reference frame A occurs before B while in the other reference frame B occurs before A.
• However, if A comes before B in one reference frame and A could be the cause of B (because light can travel from A to B in the time interval between the events), event B can never occur before A in another frame of reference.

Spacetime

• Due to such realizations, Einstein had to abandon the idea an object/event had independent positions in space and time.

• Instead, he treated them together in a single, unified 4- dimensional coordinate system – ==spacetime==.

• The path an object takes through spacetime is called its ==world line==.

  

Time Dilation

• Consider a clock that operates by counting the time it takes a light beam to bounce between two mirrors.

  

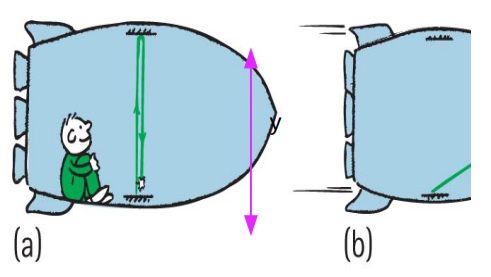
• The time it takes for the light beam to go from one mirror to the other and back again is t 0 which we will call the proper time.

• The proper time is

  • time= distance speed → t_0 = 2y / c

• To another observer in a different frame of reference, the light travels a longer path.

  

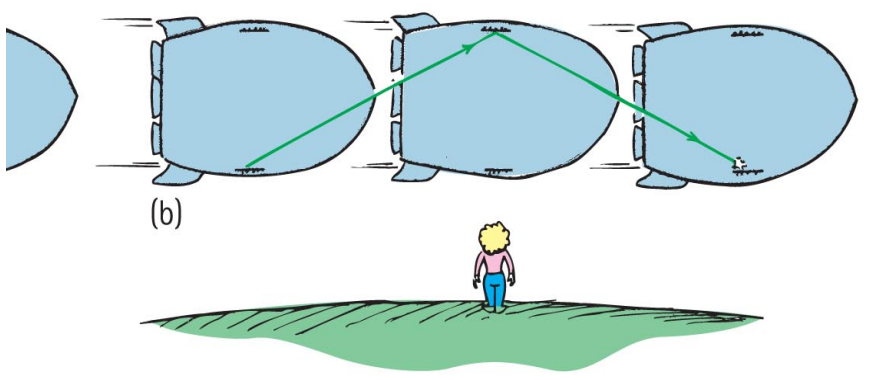
• Since the speed of light is unchanged, according to this observer the time it takes to bounce from one mirror to the other and back again must be longer.

• We call this time the relative time t.

• If the rocket is moving with speed v then the distance traveled by the light beam is found from Pythagoras

  • d=2√(y^2 +(vt/2)^2 )

• which gives for the relative time

• t= d / c = (2√(y^2 +(vt /2)^2)) / c

  

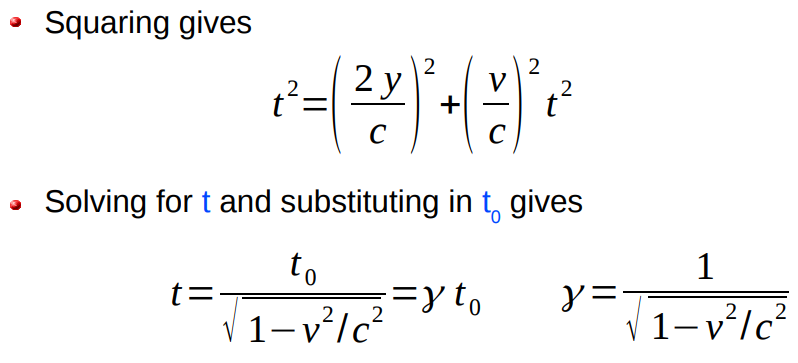
• Since γ is always bigger than one, the observer watching the clock move past measures a longer time between events.

• This effect is called time dilation.

  • Time dilation is seen in many different phenomena such as the decay of subatomic particle but also the GPS system.

• γ is called the Lorentz factor (Lorentz introduced it before Einstein)

The twin paradox

• Consider two identical twins Andy and Bob. One day Bob gets in a rocket and takes a trip at close to the speed of light and then returns home again.

• According to Andy who stayed behind, Bob ages more slowly due to time dilation but according to Bob, it is Andy who is moving and aging more slowly.

• When Bob returns, who is the younger twin?

• Let’s say the rocket has a mechanism which emits a flash of light every 6 minutes and the rocket flies at 0.6 c.

• Bob takes off in the rocket and the rocket starts emitting flashes which Andy observes using a telescope.

• Due to time dilation and the extra distance traveled between each flash, Andy sees a flash every 12 minutes.

  

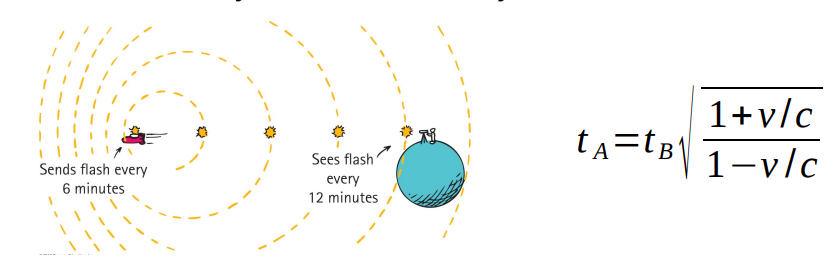
• According to Bob, when the tenth flash is emitted, 10 x 6 min = 1 hour has elapsed.

• When Andy receives the tenth flash 10 x 12 min = 2 hours has elapsed.

• After Bob’s rocket emits the tenth flash, he turns around.

• The rocket continues to emit flashes every 6 minutes but now Andy receives flashes every 3 minutes.

  • the time dilation is more than compensated by the shorter distance

  

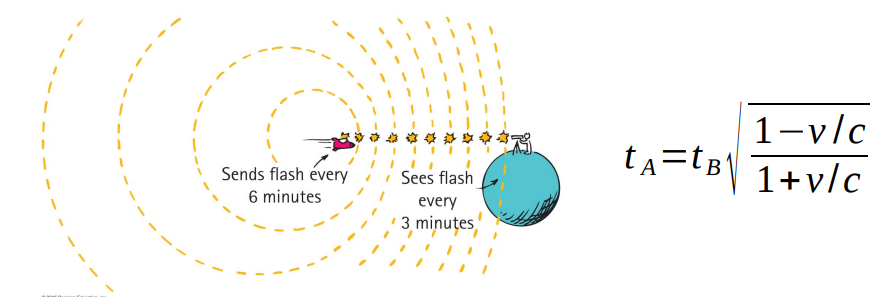
• Bob returns home just as the twentieth flash is emitted. The total journey time, according to Bob, is 20 x 6 min = 2 hours.

• According to Andy, Bob took 10 x 3 min to return giving a total journey time of 2 hours 30 min.

• Thus Andy is older than Bob by 30 minutes.

• The same conclusion is reached if it is Andy sending light flashes to Bob.

  

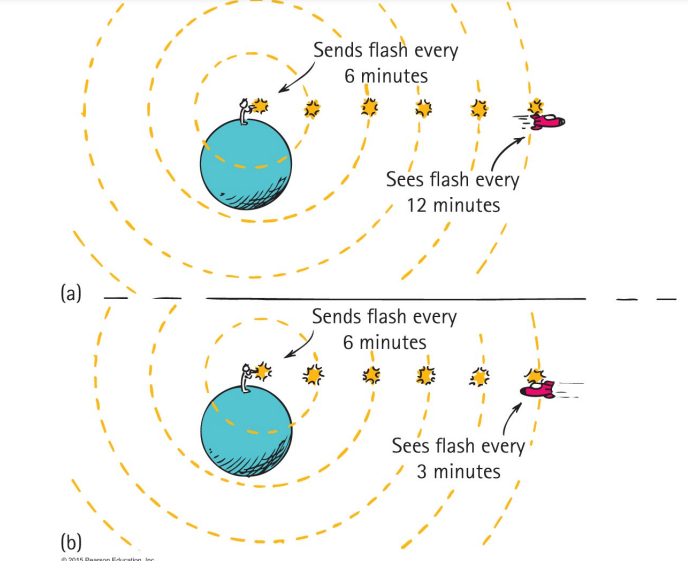
• Bob sees five flashes spaced by 12 minutes on his 1-hour outward journey, and 20 flashes separated by 3 minutes on his 1-hour inward journey.

• According to Bob, his journey time is still 2 hours.

• Andy sends 25 flashes separated by 6 minutes for a total of 2 hours 30 minutes.

• Andy is still older than Bob by 30 minutes.

Length Contraction

• An observer inside the rocket measures the length of the rocket by measuring the time it takes for a light beam to travel from the back of the rocket to the front, and then back again.

• After measuring this time, t 0 , the observer then determines the length my multiplying by the speed of light and ½.

• The length of the rocket is L0 , the proper length.

• The formula is

• distance=speed x time → 2 L0=c t0

• An observer outside the rocket who sees the rocket move past with speed v, measures different times t 1 and t 2 for the two parts of the light round trip because the rocket is moving.

• The distance traveled by the light is the length of the rocket L plus/minus the distance moved by the rocket

• c t1=L+vt1 c t2=L−vt2

  

• If we solve for the length L we find

  • L=L0√(1−v^2/c^2) =L0 / γ

• Since γ is always greater than 1, the observer watching the rocket fly past measures it to be shorter than the observer inside the rocket.

• This effect is called length contraction.

• Only the length in the direction of motion is changed, lengths in other directions do not change.

  

The train paradox

• Consider a train with a length of 500 meters when it is at rest, which is capable of traveling at 8/10 the speed of light

• The train travels over a track where there is tunnel 500 m long.

• Due to length contraction the train is shortened to 300 m so there is a period of time when the entire train is in the tunnel.

• During this period two guillotine gates at the ends of the tunnel are simultaneously lowered and raised again.

• The train is not damaged and continues down the track.

  

• But, according to a passenger on the train it is the tunnel which is shortened, not the train.

  • the length of the tunnel is 300 m, the train is still 500m.

• According to this passenger, there is no time when the entire train is inside the tunnel.

• When this passenger sees the two guillotine gates at the end of the tunnel lowered then raised again, what happens?

• The train survives.

• For the passenger in the train, the gates are not lowered simultaneously:

  • the front gate is lowered before the front of the train has passed through the tunnel,
  • the back gate is lowered after the rear of the train has entered the tunnel

EXAMPLE 1

A 70 foot long bus is driven at 0.99c. How long does the bus appear to be to someone watching it drive past?

• Using L=L0√ 1−v 2 /c 2 L=70 ft √ 1−0.992 L=9.8ft

Relative Velocity

• Back in chapter 3 we talked briefly about relative velocity

  

• In Special Relativity the velocity of an object in different reference frames is more complicated.

No math version

• Consider two objects A and B moving in a straight line in the same direction with speeds vA and vB .

• Object B sees object A with a speed vA

  

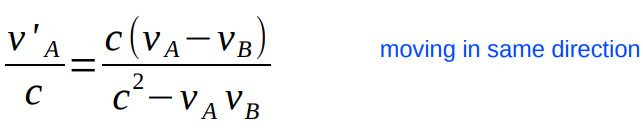
• If object B is moving in the opposite direction from object A then vB → -vB

  

Math version

• Consider two objects A and B moving in a straight line in the same direction with speeds vA and vB .

• At time zero the two objects pass each other.

• Object A emits a flash of light after a time t 0 in it’s reference frame which we observe to be t* due to time dilation.

• The flash reaches object B at a time t_F given by

  

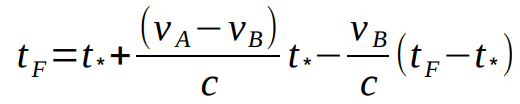
• The first term is the time we have to wait for the flash from A, the second is the distance between A and B at that time, and the third term is the correction to the second because B moves as the flash propagates towards it.

  

• Object B sees object A with a speed v’A

• According to B, the flash of light from A is emitted at time t’* and reaches it at a time t’F

  

• t * and t*’ are both time dilated relative to t0 , and tF is time dilated relative to t’_F

  

• Using these relations one finds

  

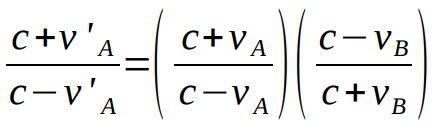
• This can be solved for v’A

  

• If object B is moving in the opposite direction from object A then vB → -vB

  

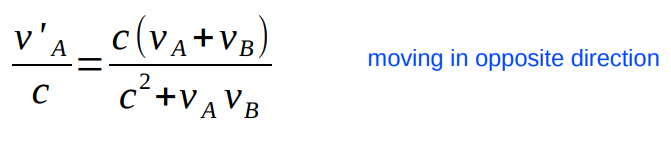
• For example: let A be moving at 0.5 c in one direction and let B be moving at 0.5 c in the opposite direction.

• In the frame of reference of object B, object A has a speed of

  

• according to B, A has a speed less than the speed of light.

• Consider another case: A is moving at the speed of light and B is moving in the same direction at 0.5 c.

• The speed of A in the frame of B is

  

• which means A still has a speed equal to the speed of light.

Mass Energy Equivalence

• While several concepts change in Special Relativity, there are also several which do not.

  • Newton’s First Law remains valid: if there are no external forces then an object does not accelerate.
  • Newton’s Third Law also remains valid: for every action there is an equal and opposite reaction.

• What has to change is any law or quantity that involves rates of change e.g. involves a velocity.

  • so this includes momentum and kinetic energy.

• BUT the new definitions have to approach the old ones as the velocity of an object becomes small.

• This requirement is called the correspondence principle.

• The momentum of an object with speed v is redefined to be

  • p=γ m_0 v

• m_0 is the object’s rest mass - the mass it has when it is at rest - and γ the Lorentz factor is

  • γ = 1 √(1−v^2 /c^2)

• When the speed v is small γ → 1 so the new definition of momentum matches the previous, Newtonian, one.

• But as the speed becomes large the relativistic momentum becomes very large.

• What this means is that it becomes very difficult to deflect a particle which is moving at close to the speed of light.

• The combination γm0 is called the object’s apparent mass written as m.

  • m=γ m_0

• Using this definition means the relativistic definition of momentum looks exactly like the Newtonian.

  • p=m v

• Einstein also had to redefine the energy of an object.

• His redefinition was that the energy E of an object with rest mass m0 , speed v and relativistic momentum p is

• E^2 = p^2 c^2 + m_0^2 c^4

  

• E=m c^2

• The energy of an object at rest, its rest mass energy, is

  • E0=m0 c^2
  • which is not zero.

• This Einsteinian definition of energy is not the kinetic energy.

• The kinetic energy is the energy a moving object has in addition to its rest mass energy.

  • K=E−m_0 c^2

• In the limit where the speed v is small this approaches

• K= 1/2 m_0 v^2

• E = m c^2 can be interpreted as being

• m= E / c^2

• that is, if we know the total energy of an object, this formula gives its effective mass (multiply by g to get its weight).

• ==Anything which changes the energy of something changes the mass.==

• For example: when a chemical reaction occurs, energy is released. The energy of the products is less than the energy of the reactants so the mass of the products is also less than the mass of the reactants.

  • the mass difference is very small because c2 is a very big number.

• When the atomic bomb exploded over Hiroshima, 66.9 TJ of energy was released.

• This corresponds to a mass of 1 g – a packet of sugar.

• The energy output of the Sun is 3.846 x 1026 W which is generated by reactions that combine hydrogen to make helium.

• This energy output corresponds to a mass of 4,270,000 tons every second.

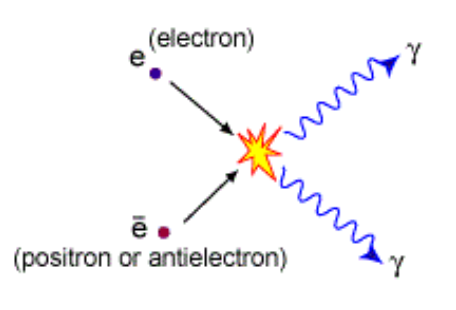
• Perhaps the most dramatic demonstration of the mass-energy relation is the case of electron-positron annihilation.

  • A positron is an antimatter particle: it has the same mass of an electron but a positive charge, not negative.

• Positrons are created in some decays of radioactive nuclei as well as in collisions between nuclei.

• When an electron encounters a positron the two particles are annihilated to light, all the initial mass is lost.

  

\

EXAMPLE 1

Which is heavier, a fully charged phone or one that needs to be recharged?

• Strictly speaking, ==the fully charged phone would weigh slightly more== than the one that needs to be recharged, according to Einstein's theory of mass-energy equivalence (E=mc²). However, the difference in weight would be so tiny that it would not be measurable with any available technology. In practical terms, the weight difference between a fully charged phone and one that needs to be recharged is negligible and can be considered equal.

EXAMPLE 2

A golf ball is weighed at the top of a skyscraper and then dropped off the edge. After it falls to the ground, it is weighed again. How does its mass compare with the mass measured at the top of the skyscraper?

• The mass of the golf ball remains the same, regardless of its velocity or position. However, its ==weight will appear to increase when measured at the top of the skyscraper== due to the effects of gravity. As it falls, the weight will decrease due to the decrease in distance from the center of the Earth and the decrease in gravitational force, but the mass will remain constant. This phenomenon is explained by the equivalence of mass and energy, as described by Einstein's theory of relativity.

EXAMPLE 3

A bus weighs 10,000 kg when it is at rest. When it is traveling at 50 m/s, what is its mass? When it is traveling at 0.99c, what is its mass?

• Using m=γ m0 m= m0 √ 1−v 2 /c 2 m= 10, 000 kg √ 1−(50ms −1 /3 x108 ms −1 ) 2 =10 , 000.0000000001 kg m= 10 , 000 kg √ 1−(0.99) 2 =
• ==17,864 kg==

\