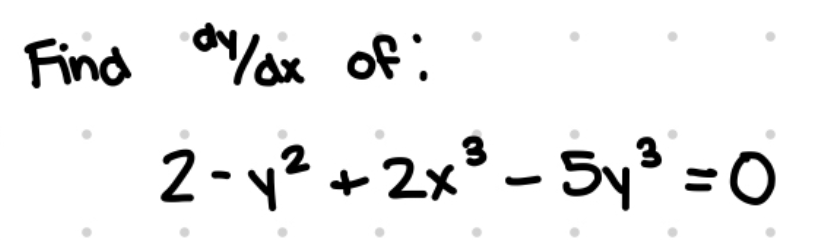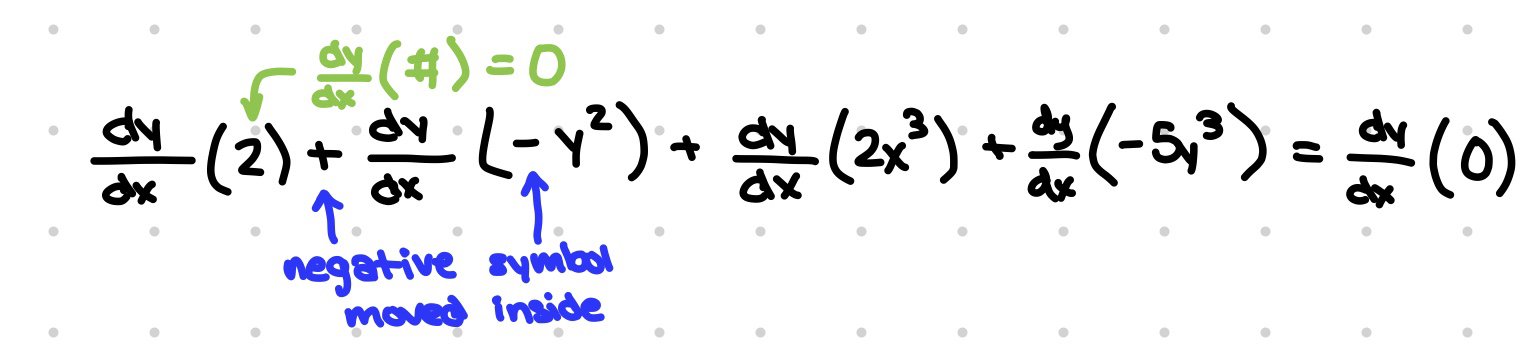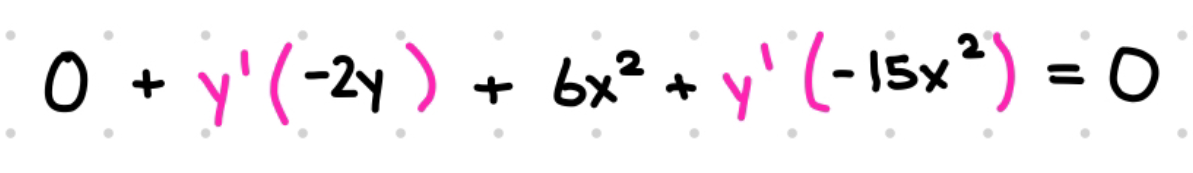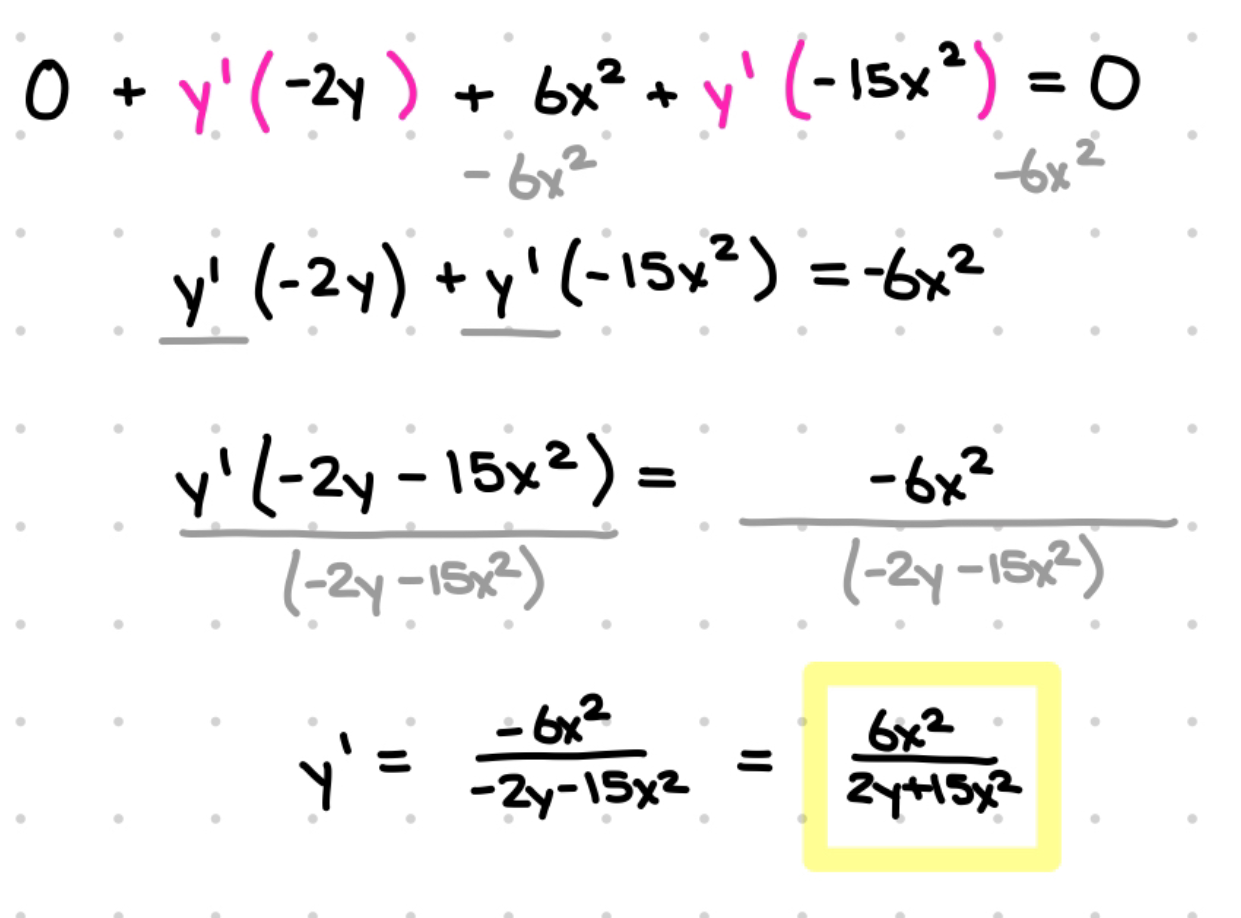Implicit Derivatives (with problem walkthrough)

☝️ What to Know Already

• What dy/dx and y’ mean

• Derivatives with dy/dx, a function of x is defined as y (such as y = x^2)

• Power rule, chain rule, derivative functions with operators (+ - * /)

🤔 Explicit vs Implicit

Explicit derivatives are clear in that they present themselves as a function of one variable, usually y or f(x).

• An example of an explicit function is y = 2x, as we can clearly see the function is y.

Implicit derivatives aren’t as clear as they place the variable y or f(x) inside of the problem.

• An example of an implicit derivative problem would be dy/dx(2x + 3y = 25)

💡The Rule

To solve for an implicit derivative of dy/dx, differentiate all terms. To do so,

1. Differentiate terms with a coefficient of x as normal.

• If a problem had “x^2” as a term, you would differentiate it as usual: 2x

2. Multiply terms with a coefficient of y by y’ after applying regular derivative rules to them.

• If a problem had “y^2” as a term, you would differentiate it as if y was x, then multiply it by y’: 2y(y’)

Our final answer should be equal to y’.

✍️ Tackling a Problem

Let’s look at a problem with implicit derivative rules. You can find a summary at the bottom.

When we have the variable y, but y is also the function (dy/dx), we have to use implicit derivative rules.

Terms like 2x^3 can be quickly cleaned up with the power rule, but we have to multiply terms such as -y^2 by y’.

Once we do this, we aim to isolate y’ in order to find the derivative. Remember that “dy/dx of y” and “y’” mean the same thing.

That gives us our final answer.

Here’s our full work: