
Amount of Substance (3.1.2)
Relative Atomic Mass and Relative Molecular Mass
Specification Points:
Relative atomic mass and relative molecular mass in terms of 12C.
The term relative formula mass will be used for ionic compounds.
Students should be able to:
define relative atomic mass (Ar)
define relative molecular mass (Mr)
Relative atomic mass is the ratio of the mass of an element to 1/12 th of the mass of a carbon atom.
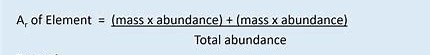
The relative molecular mass (Mr) is the average mass of a molecule relative to one twelfth of the mass of an atom of carbon-12.
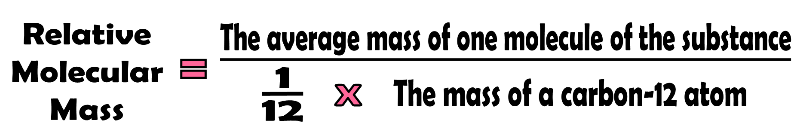
The Mole and the Avogadro Constant
Specification Points:
The Avogadro constant as the number of particles in a mole.
The mole as applied to electrons, atoms, molecules, ions, formulas and equations.
The concentration of a substance in solution, measured in mol dm–3.
Students should be able to carry out calculations:
using the Avogadro constant
using mass of substance, Mr, and amount in moles
using concentration, volume and amount of substance in a solution.
Students will not be expected to recall the value of the Avogadro constant.
Avogadro’s Constant:
6.02 × 10^23
Equations:
Number of particles = Number of moles × Avogadro’s constant
Example: How many atoms are in 0.450 moles of pure iron?
Number of atoms = 0.450 × (6.02 × 10^23) = 2.71 × 10^23
Number of moles = mass of substance /Mr
Example: How many moles of aluminium oxide are present in 5.10 g of Al2O3?
Mr of Al2O3 = (2 × 27.0) + (3 × 16.0) = 102
Number of moles of Al2O3 = 102 /5.10 = 0.0500 moles
Moles and concentration
The concentration of a solution is how many moles are dissolved per 1 dm3 of solution. The units are mol dm–3.
Here’s the formula to find the number of moles.
Number of moles = Concentration × Volume (in cm3)/1000
or
Number of moles = Concentration × Volume (in dm3)
Ideal Gas Equation
Specification Points:
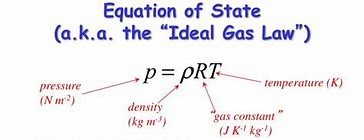
The ideal gas equation pV = nRT with the variables in SI units.
Students should be able to:
use the equation in calculations.
Students will not be expected to recall the value of the gas constant, R
if you’re given the values in different units from the ones used in the ideal gas equation, you’ll need to convert them to the right units first.
You might be given pressure in kPa (kilopascals). To convert from kPa to Pa you multiply by 1000 (e.g. 2 kPa = 2000 Pa).
You might be given temperature in °C. To convert from °C to K you add 273 (e.g. 25 °C = 298 K).
You might be given volume in cm3 or dm3 . To convert from cm3 to m3 you multiply by 10–6. To convert from dm3 to m3 you multiply by 10–3 . (1 m3 = 1 × 106 cm3 = 1 × 103 dm3 )
Empirical and Molecular Formula
Amount of Substance (3.1.2)
Relative Atomic Mass and Relative Molecular Mass
Specification Points:
Relative atomic mass and relative molecular mass in terms of 12C.
The term relative formula mass will be used for ionic compounds.
Students should be able to:
define relative atomic mass (Ar)
define relative molecular mass (Mr)
Relative atomic mass is the ratio of the mass of an element to 1/12 th of the mass of a carbon atom.
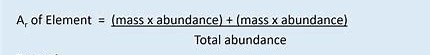
The relative molecular mass (Mr) is the average mass of a molecule relative to one twelfth of the mass of an atom of carbon-12.
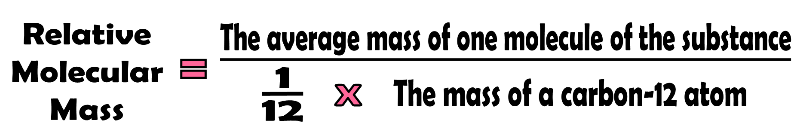
The Mole and the Avogadro Constant
Specification Points:
The Avogadro constant as the number of particles in a mole.
The mole as applied to electrons, atoms, molecules, ions, formulas and equations.
The concentration of a substance in solution, measured in mol dm–3.
Students should be able to carry out calculations:
using the Avogadro constant
using mass of substance, Mr, and amount in moles
using concentration, volume and amount of substance in a solution.
Students will not be expected to recall the value of the Avogadro constant.
Avogadro’s Constant:
6.02 × 10^23
Equations:
Number of particles = Number of moles × Avogadro’s constant
Example: How many atoms are in 0.450 moles of pure iron?
Number of atoms = 0.450 × (6.02 × 10^23) = 2.71 × 10^23
Number of moles = mass of substance /Mr
Example: How many moles of aluminium oxide are present in 5.10 g of Al2O3?
Mr of Al2O3 = (2 × 27.0) + (3 × 16.0) = 102
Number of moles of Al2O3 = 102 /5.10 = 0.0500 moles
Moles and concentration
The concentration of a solution is how many moles are dissolved per 1 dm3 of solution. The units are mol dm–3.
Here’s the formula to find the number of moles.
Number of moles = Concentration × Volume (in cm3)/1000
or
Number of moles = Concentration × Volume (in dm3)
Ideal Gas Equation
Specification Points:
The ideal gas equation pV = nRT with the variables in SI units.
Students should be able to:
use the equation in calculations.
Students will not be expected to recall the value of the gas constant, R

if you’re given the values in different units from the ones used in the ideal gas equation, you’ll need to convert them to the right units first.
You might be given pressure in kPa (kilopascals). To convert from kPa to Pa you multiply by 1000 (e.g. 2 kPa = 2000 Pa).
You might be given temperature in °C. To convert from °C to K you add 273 (e.g. 25 °C = 298 K).
You might be given volume in cm3 or dm3 . To convert from cm3 to m3 you multiply by 10–6. To convert from dm3 to m3 you multiply by 10–3 . (1 m3 = 1 × 106 cm3 = 1 × 103 dm3 )
 Knowt
Knowt