AP Bio Unit 4 Genetics

Chapter 10 Meiosis

Vocab Terms:

• Synapsis- the pairing of homologous chromosomes during prophase I

• Synaptonemal complex- zipper-like structure composed of proteins connects a homologous chromosomes together tightly along their lengths during part of prophase I

• Karyotype- display of a COMPLETE SET OF chromosome pairs of a cell arranged by size/shape

• Recombinant chromosome- created when crossing over combines DNA from parents into a a single chromosome

• Gene- Segments of DNA that encode heritable characteristics (traits) passed on from parent to offspring

• Allele- the different forms of a gene

• Locus- the LOCATION of a gene on a chromosome

• Tetrads- Homologous chromosome pairs

• Chromosome- Thread-like structures that contain genes and carry a molecule of DNA

  • Homologous chromosomes- A pair of chromosomes SIMILAR in size and shape

• Chromatid- A single half of a chromosome (chromosome comes in set of 2 sister chromatids)

• Chromatin- the complex of DNA and proteins that serve as the BUILDING MATERIAL for chromosomes when wound up into coils

• Genome- An entire (haploid) set of chromosomes found in a cell

• *Sporophyte- the diploid, multicellular stage of the plant that produces haploid spores by meiosis (like gametes produced in animals plants produce spores)

• Haploid (n) one set of chromosomes (23) NO HOMOLOGOUS PAIRS

  

Meiosis Steps

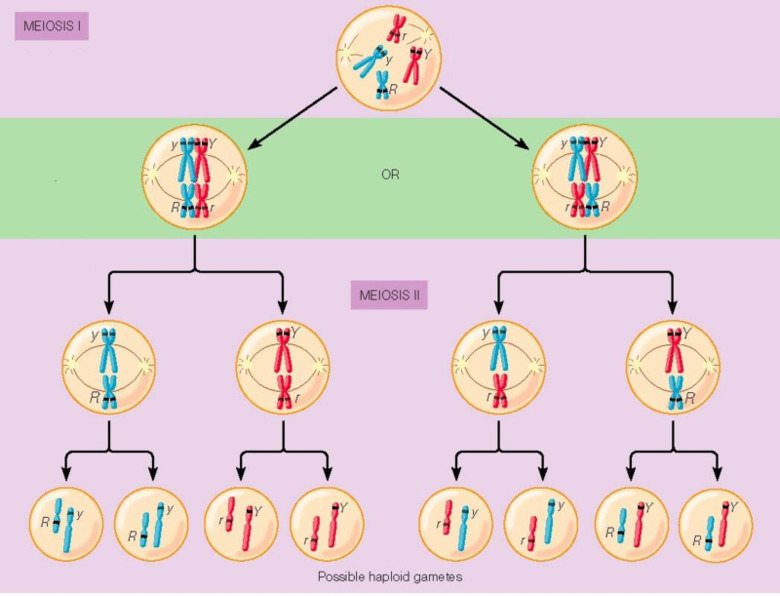
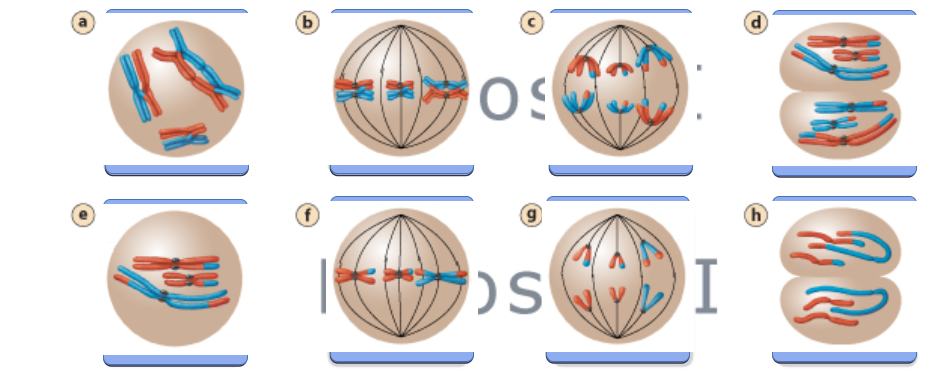
Meiosis I

This stage separates homologous chromosomes, reducing the chromosome number from diploid (2n) to haploid (n).

1. Prophase I

   • Chromosomes condense and become visible.

   • Homologous chromosomes pair up in a process called synapsis, forming tetrads (Homologous chromosome pairs)

   • Crossing over occurs at chiasmata, increasing genetic diversity.

   • The nuclear envelope breaks down, and spindle fibers begin to form.

2. Metaphase I

   • Homologous chromosome pairs (tetrads) align along the metaphase plate and are attached to the spindle apparatus.

   • Independent Assortment- random orientation of homologous pairs on the equator

   • Calculating possible configurations: Based on n of pairs of homologous chromosomes 2^n ex. n = 3 then there would be 8 possible configurations

     • NOT 2^6 because in Metaphase I separate based on homologous chromosome pairs

   • Spindle fibers attach to centromeres of homologous chromosomes.

3. Anaphase I

   • Homologous chromosomes are pulled apart to opposite poles of the cell.

   • Sister chromatids remain attached at their centromeres.

     • Different from mitosis where sister chromatids separate

4. Telophase I and Cytokinesis

   • Chromosomes reach the poles, and the nuclear membrane may reform.

   • The cell divides into two each contains HALF the original number of chromosomes Ex. 4 → 2 or 2 pairs → 1 pair

   • Cell divides into TWO haploid daughter cells—NO HOMOLOGOUS PAIRS because separated in prior steps

Meiosis II (Equational Division)

This stage separates sister chromatids, similar to mitosis.

1. Prophase II

   • Similar to prophase of mitosis except no DNA replication prior

   • Chromosomes condense again if they had decondensed.

   • The nuclear envelope dissolves, and spindle fibers reform.

2. Metaphase II

   • Chromosomes align at the metaphase plate, similar to mitosis.

   • Spindle fibers attach to centromeres (center) on each chromatid

3. Anaphase II

   • Sister chromatids are finally pulled apart to opposite poles.

4. Telophase II and Cytokinesis

   • Nuclear membranes reform around each set of chromosomes.

   • The cytoplasm divides, resulting in FOUR haploid daughter cells, each genetically unique containing chromatids.

Mechanisms contributing to genetic variation:

• Errors (mutations) in DNA replication

• Separation of sister chromatids in meiosis II

• Fertilization- random fusion of male & female gametes

• Independent assortment- homologous chromosomes randomly lined up during Metaphase I to be separated into gametes later

  

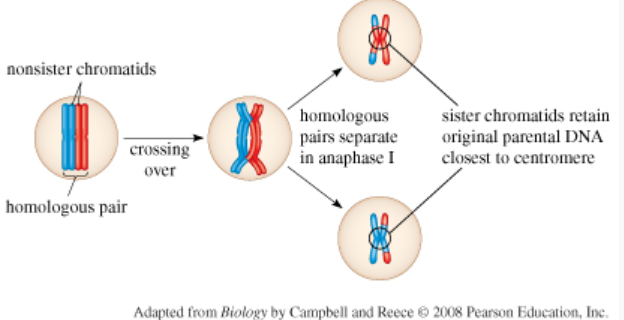
• Crossing over producing new chromosome combinations

  • Occurs in Prophase 1 at the chiasmata main purpose is the produce genetic variation

  • Also important for synapsis to occur correctly—matching of homologous chromosome pairs to ensure each cell receives one complete set of chromosomes

  • Typically occurs at the ends of chromosomes—retain DNA near centromere

  • Homologous chromosomes must align precisely so that non-sister chromatids can exchange corresponding segments of DNA

  • As a result of crossing over, sister chromatids are no longer identical

  

Concept 10.1

• Asexual reproduction occurs when a sole parent passes copies of all genes to offspring without gamete fusion → creating a clone (genetically identical individuals)

Concept 10.2 Fertilization and Meiosis alternate in sexual life cycles

• Normal human somatic cells (body cells, non-sex cells) are diploid (2 sets of chromosomes) with n = 46 chromosomes, one set inherited from each parent

• Diploids have 22 homologous pairs (44 chromosomes) autosomes and one pair of sex chromosomes that help determine the sex of the person (XX vs XY)

• Reproductive organs produce haploid gametes through meiosis—each gamete is haploid with one set of n = 23 chromosomes

• During fertilization gametes (egg and sperm) combine to form a diploid zygote with 2 sets of chromosomes n = 46 that develops into an organism via mitosis

Chapter 11 Mendelian Genetics

Vocab Terminology

• Character: A heritable feature that varies among individuals (i.e. color)

  • Quantitative character- heritable feature that continuously varies over a range of values (can be quantified) (i.e. height, weight, blood pressure)

• Each variant for a character (i.e. white flowers vs purple flowers)

• *Epistasis- interaction between alleles of DIFFERENT genes where phenotypic expression of one gene alters that of another gene—one gene masks the expression of another (ex. aacc same as AAcc if c is epistatic to A)

• *Pleiotropy- ability of a SINGLE gene to have multiple effects

• Hybridization- crossing of two TRUE-BREEDING varieties

• Generations: P generation—parents; F1 generation—first filial generations cross from parents; F2 generation—second filial generation crossing F1 generations

• Polygenic inheritance: Phenotype controlled by multiple genes rather than one

  • Multifactoral: phenotypic character influenced by multiple genes/environmental factors

• Mendel’s Model

• 1) Alleles/alternative versions of genes account for variations in inherited characters

  • Results from slight variations in nucleotide sequence along chromosomes

• 2) For each character, an organism inherits TWO versions of a gene, one from each

• 3) If two alleles in an organism differ (heterozygous), then one is a dominant allele that determines the organism’s appearance and the other recessive allele has no noticeable effect

• 4) Law of segregation—the two alleles segregate (separate from each other) during gamete formation and end up in different gametes; Used for monohybrid cross

  • Egg/sperm gets only one of the two alleles present in somatic cells of the organism (i.e. with heterozygous 50% of gametes receive dominant and 50% receive recessive allele)

  • In the case of the heterozygous green-pod plant (Gg), one gamete will receive the dominant allele (G), and the other gamete will receive the recessive allele (g)

  • 

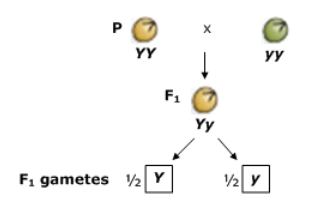
• Heterozygote—has two different alleles for a gene (heterozygous); homozygote—same alleles for a gene (homozygous)

• Phenotype- the appearance/observable traits (purple or white)

• Genotype- the genetic makeup (PP, Pp, pp)

Testcross

• Used to determine the genotype of an unknown dominant trait (whether it is homozygous or heterozygous) by crossing with a recessive

  • If homozygous all offspring will show the dominant trait because dominant allele is always present; if heterozygous, half of the offspring will show the recessive trait

    

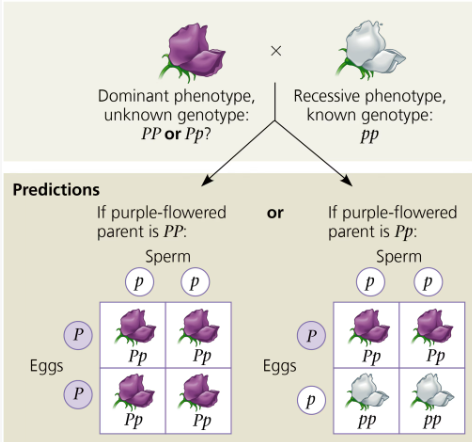
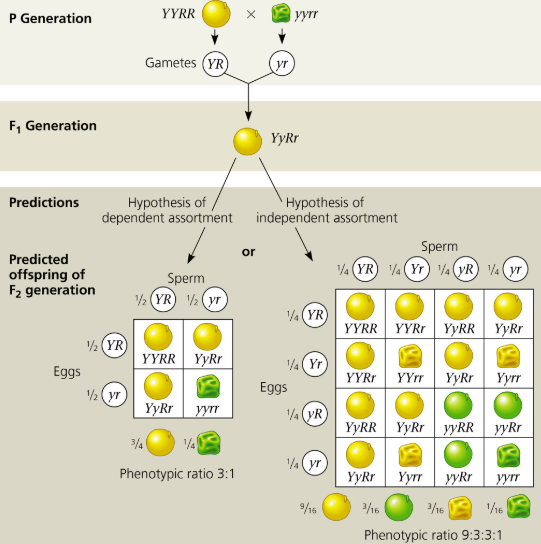
Law of Independent Assortment

• Law of Independent Assortment—two or more genes assort independently—each pair of alleles segregates independently during gamete formation; Used for dihybrid cross

• 

• Law of Segregation based on a SINGLE character with all F1 generations being monohybrids—heterozygous for one particular being followed in the cross (Monohybrid cross)

• Dihybrids- individual heterozygous for TWO characters being followed in the cross (Dihybrid cross)

  • 

Statistics of Inheritance—laws of probability govern mendelian inheritance

Multiplication Rule-

• Probability that 2+ INDEPENDENT events will occur together in a specific combination → multiply probabilities of each event

  • Ex. Crossing AABbCc x AaBbCc probability of AaBbcc

  • Probability of each TRAIT (denoted by the different letters A, B, C ) → ½ (A) x ½ (B) x ¼ (C) = 1/16

    • AA x Aa = 50% chance of Aa or AA; Bb x Bb = 50% chance of Bb and 25% chance of BB or bb; Cc x Cc = 50% chance of Cc and 25% chance of cc or CC

  • Ex. Crossing Rr x Rr to get RR or rr

    • ½ probability for carrying dominant allele (R) or recessive (r ) probability that you will get TWO recessive alleles present is ½ x ½ = ¼

  • Using Multiplication rule for Dihybrid Cross

    1. Use monohybrid cross to find probability of each INDIVIDUAL trait

    2. For each of the 4 possible combinations, multiply together the ratios of the respective individual traits

  • 

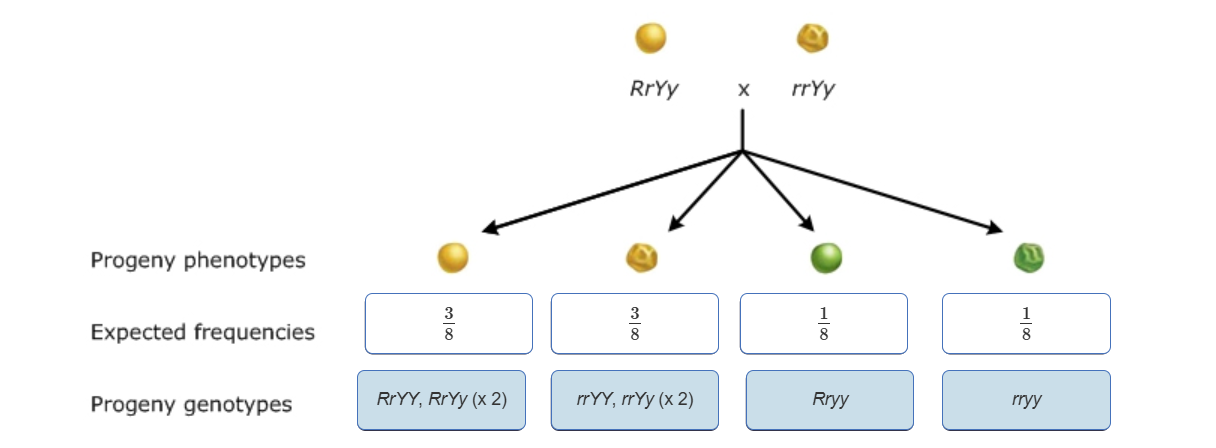
Addition Rule-

• Probability that 2+ MUTUALLY EXCLUSIVE events will occur → add together individual probabilities

  • Ex. Throwing a die landing on a 4 OR 5 → 1/6 + 1/6 = 1/3

  • Ex. Crossing Rr x Rr to get Rr

    • ½ probability of rR and ½ probability of Rr → ¼ + ¼ = ½

More Complex Genetics

• Incomplete Dominance- When hybrids (heterozygous) have an appearance BETWEEN that of 2 parents (i.e. red x white = pink) (i.e. C^R and C^W)

  • Complete Dominance- heterozygote & homozygote for dominant allele are indistinguishable

• Codominance- phenotype of BOTH alleles is expressed (i.e. red hair x white hair = roan horses)

  • Indicated not by capital/lowercase but by exponent (i.e. L^M vs L^N)

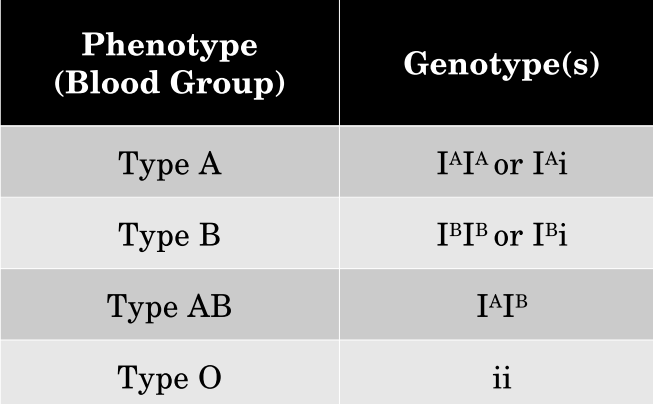
• Multiple Alleles- Gene has 2+ alleles for the trait

  • Ex. Human ABO blood groups

    • I^A, I^B, i: I^A & I^B are Codominant creating type AB blood; i is recessive creating type O blood

      

Chi-Squared (X²) test

• Used to determine if there is a significant difference between the expected and observed data

• Null Hypothesis- NO statistically significant different between expected and observed data

• Formula:

  X² = the sum of (O - E)²/E; Observed frequencies, Expected frequencies

• Steps:

  1. Determine the null hypothesis

  2. Use formula to calculate the X² value

     • n = number of categories, e = expected frequency/value, o= observed frequency/value

     • Calculate expected frequency/count—multiple total by expected percentage to get numbers

     • Plug into formula (observed value - expected value)²/expected value

     • Add all together for X² value

     • Find df with number of categories - 1

  3. Find critical value using table (Use p = 0.05 (default) or p = 0.01)

     • P-value probability- how often our results could happen due to change

     • Degrees of freedom (df) = n - 1

  4. If X² < critical value…FAIL to reject the null hypothesis

     • Differences in data due to change

     If X² > critical value…reject the null hypothesis

     • Differences in data NOT due to chance

Example

• Total M&M’s—100; 6 types of M&M’s each color has 20; Claimed percentage - 14% yellow

• Expected frequencies- Total * (Percent/100)

• Calculation:

  (O-E)²/E = (20 - 14)²/14 = 2.57…. add all M&M’s together to get SUM(X²) = 21.01

  df = n - 1 = 6 - 1 = 5

  p = 0.05

  critical value = 11.07 (look on table using p value and degrees of freedom)

  RESULT: 21.01 > 11.07 we REJECT the null hypothesis because X² > critical value

General Rules

• Crossing 2 heterozygous Xx & Xx:

  • Phenotype: 3:1 ratio— ¾ dominant phenotype and ¼ recessive phenotype

  • Genotype: 50% chance of heterozygous (Xx) 25% chance of homozygous dominant, 25% chance of homozygous recessive (XX or xx)

• Crossing homozygous and heterozygous:

  • Phenotype: 1:1 ratio. ½ chance of heterozygous (Xx) ½ of homozygous same as homozygous parent alleles (either dominant or recessive)

• Heterozygous Dihybrid cross PpRr x PpRr

  • Phenotype: 9:3:3:1; 9 Dominant trait for both (Pp/PP + Rr/RR) 3 Dominant/recessive trait (Pp/PP + rr) 3 Dominant/recessive trait (pp + Rr/rr) + 1 recessive for both (pprr) 16 total

• Heterozygous x Homozygous Dihybrid cross PpRr x pprr:

  • Phenotype: 1:1:1:1 ratio 4/16 4/16 Dominant trait for both (Pp/PP + Rr/RR) 4/16 Dominant/recessive trait (Pp/PP + rr) 4/16 Dominant/recessive trait (pp + Rr/rr) + 4/16 recessive for both (pprr) 16 total

Parent genotypes from progeny

• Assuming (R) is smooth (r ) is wrinkled; (Y) is yellow (y) is green

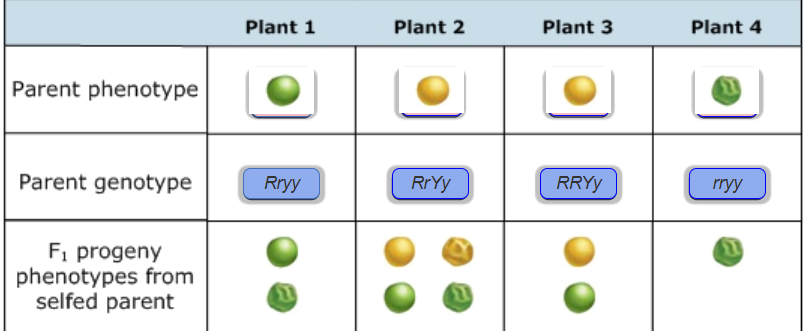
Punnett Square Predictions

• Given the parent combination is Yy x Yy and yellow (Y) is dominant

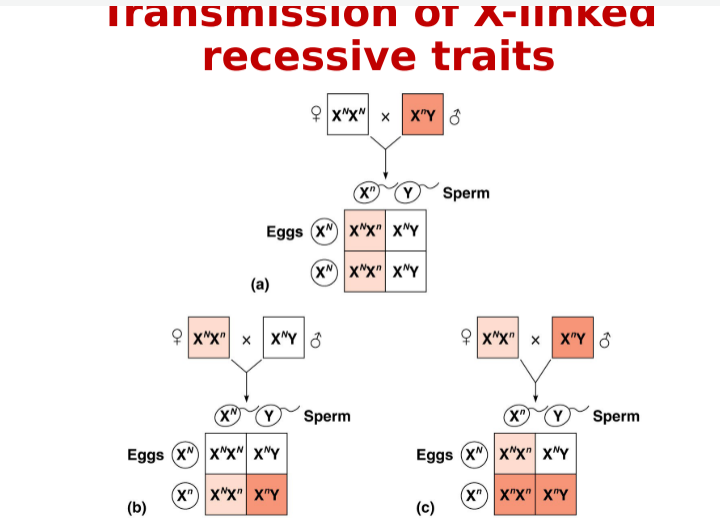
Sex-Linked Chromosomes

• Sex chromosomes carry sex-linked genes (MAJORITY ON THE X CHROMOSOME) males who inherit a recessive sex-linked

• Sex-linked gene: Located on X or Y chromosome

• Barr body- Inactive X chromosome; regulate gene dosage in FEMALES during embryonic development (when there is XX)

  

Linkage Maps

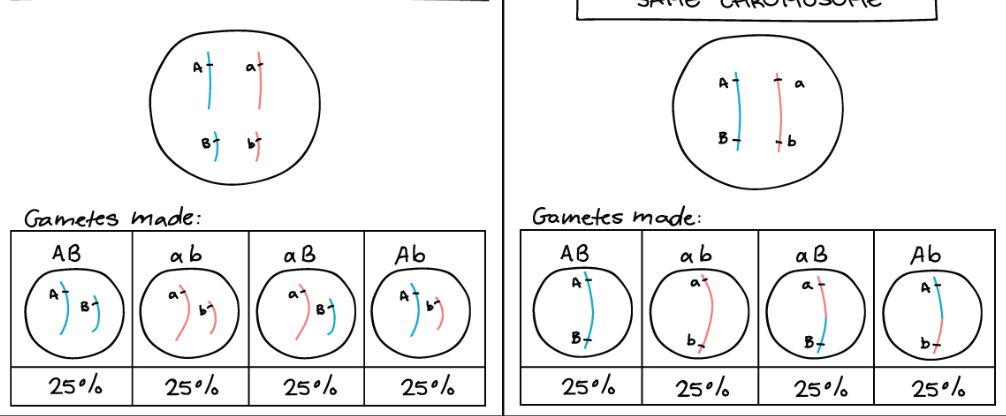
• Genes on different chromosomes/far apart assort independently and are UNLINKED

• Genes closer together are LINKED- alleles together on one chromosome inherited as a unit often

• Recombination frequency- used to check if two genes are linked

• 1 map unit = 1% recombination frequency

• 50% recombination = FAR APART on the same chromosome/2 different chromosomes

• Usually genes assort independently (allele received for one doesnt affect another) in a double heterozygous (AaBb) results in formation of 4 types of gametes with equal ¼ frequency (Combine the A alleles with the B alleles)

  • This is caused by the random orientation of homologous chromosome pairs during meiosis—independent assortment

    • 

• Genes CLOSE TOGETHER (linked) DO NOT ASSORT INDEPENDENTLY they tend to stick together during meiosis

  • Most likely to contain parental configurations (alleles already together on the chromosome prior to meiosis) rarely contain recombinant configuration (results from crossing over)

  • DO NOT follow Mendel’s Law of Independent Assortment

    • 

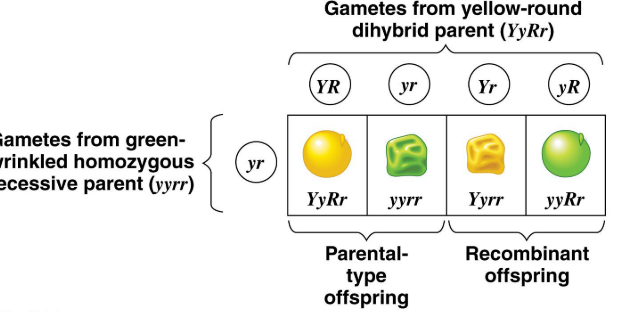
Gene Recombination

• Production of offspring with combinations of traits different from either parent; Similar to parent → Parental; Different from parents → Recombinant

  • 

• Finding recombinant frequency = # of Recombinants/total # offspring x 100%

• MAX recombinant frequency percentage is 50%

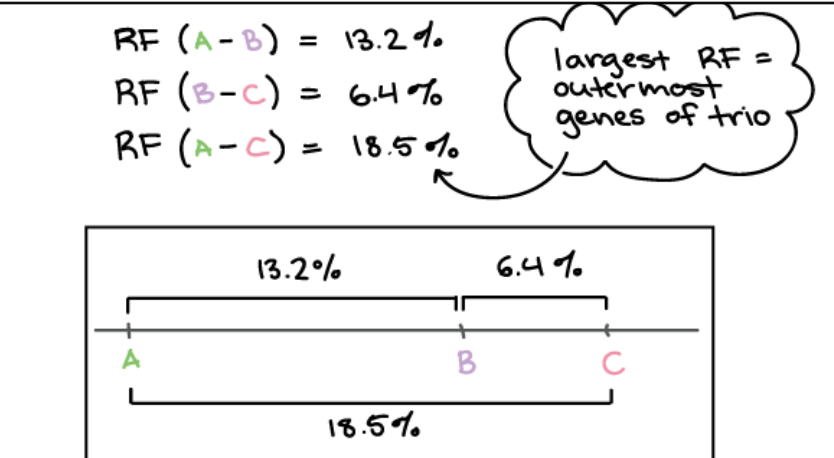
• Using recombinant frequency to find order of genes

• Ex A, B, C genes divide into three possible pairs (AC, AB, BC) to figure out which ones lie furthest apart → pair of genes with the largest recombination frequency must flank the third gene

  •