G11-Gen-Math-L-01-Q1-Functions-and-Their-Graphs

Functions and Their Graphs

Relations

Definition

• A relation is a connection or association between two or more entities.

• In mathematics, it refers to a set of ordered pairs.

Properties of Relations

• Domain: The set of all first elements (inputs) in the ordered pairs.

• Range: The set of all second elements (outputs) in the ordered pairs.

• Cardinality: The number of elements in a relation.

Conclusion

Relations are fundamental concepts that appear in various fields, including mathematics, social sciences, and computer science. Understanding their types and properties is crucial for analyzing connections and interactions in different contexts.

Definition of a Function

• A function is a relation that assigns exactly one output (y) for each input (x).

• Notation: ( f: X \rightarrow Y ) where ( X ) is the domain and ( Y ) is the codomain.

Components of a Function

1. Domain: Set of all possible input values (x).

2. Range: Set of all possible output values (y).

3. Rule: The specific operation that relates inputs to outputs.

Types of Functions - Grade 11 General Mathematics

1. Definition of Functions

• A relation where each input has exactly one output.

• Notation: f(x) represents a function with input x.

2. Types of Functions

A. Relation Graph

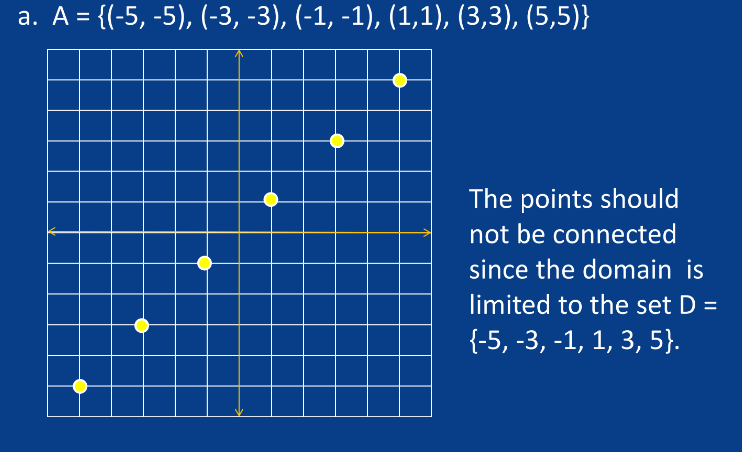
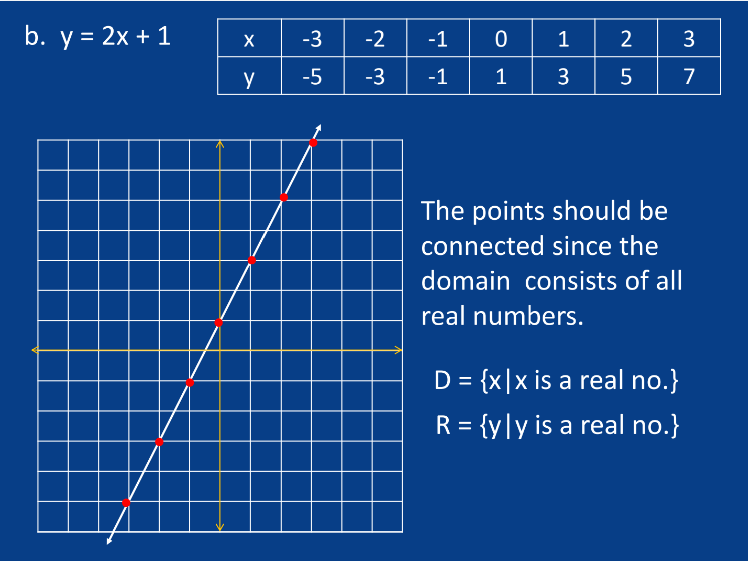
B. Linear Functions

• Form: f(x) = mx + b

  • m = slope

  • b = y-intercept

• Characteristics:

  • Graph is a straight line.

  • Constant rate of change.

    

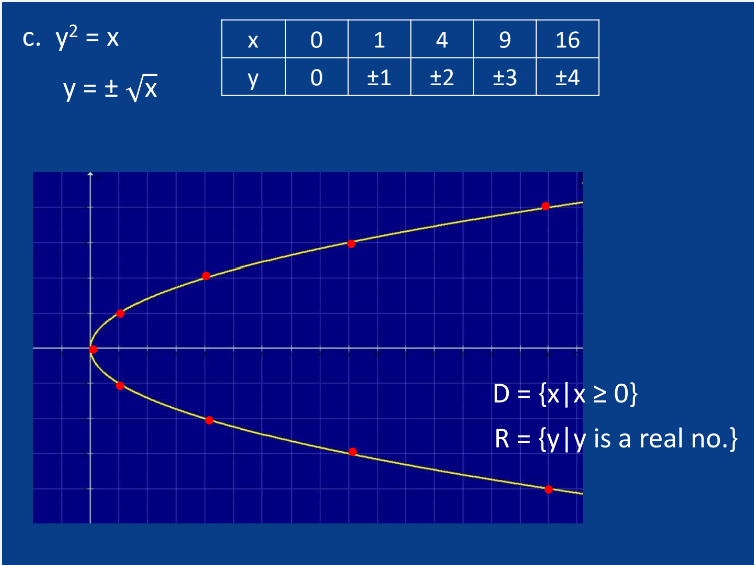
C. Parabola

• y2 = x

• Characteristics:

  • Graph is a parabola.

  • Opens upward (a > 0) or downward (a < 0).

  • Vertex and axis of symmetry.

    

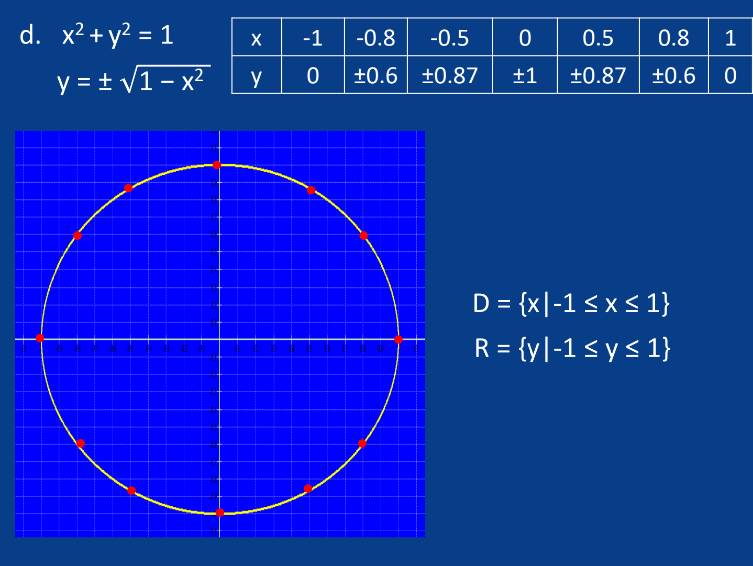
D. Circular (?) Functions

• Form: 2 + y2 = 1

• Characteristics:

  • Forms a whole circle

    

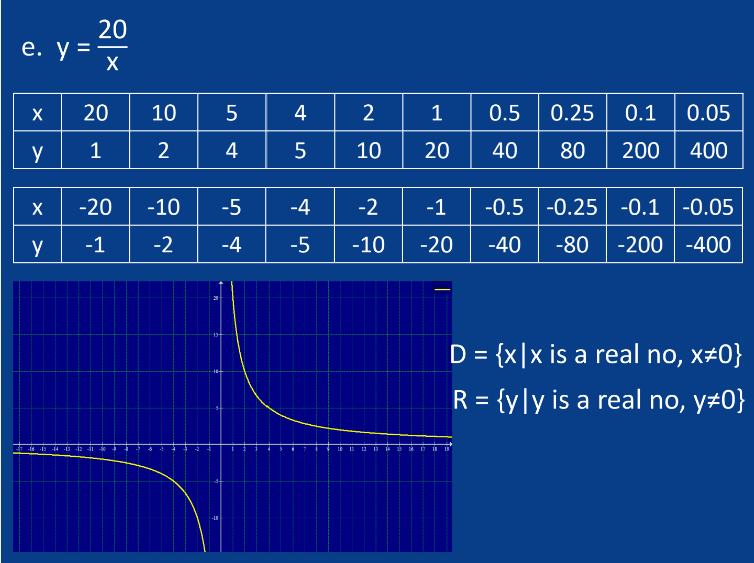
E. Rational Functions

• Form: f(x) = P(x)/Q(x) where P and Q are polynomials.

• Characteristics:

  • Can have vertical and horizontal asymptotes.

  • Undefined at points where Q(x) = 0

    .

    

E. Exponential Functions

• Form: f(x) = a*b^x

  • a > 0, b > 0, b ≠ 1

• Characteristics:

  • Rapid growth or decay.

  • Graph passes through (0, a).

• Characteristics:

  • Inverse of exponential functions.

  • Graph increases slowly.

Graphing Functions

• Axes: Use Cartesian coordinates (x-axis and y-axis).

• Plotting Points: Calculate values of ( f(x) ) for selected ( x ) values.

• **Connecting

The Vertical Line Test

A graph of a relation is a function if any vertical line drawn passing through the graph intersects it at exactly one point.

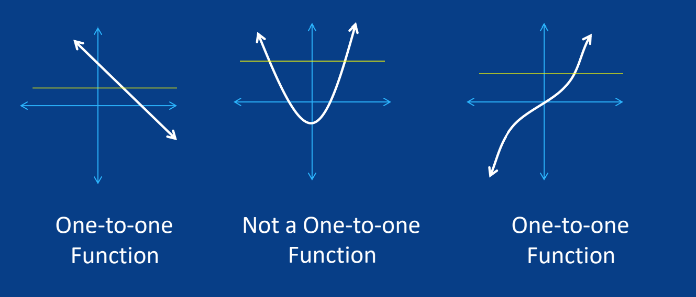
One-to-one Function

A one-to-one function is a function if any horizontal line drawn passing through the graph intersects it at exactly one point.

Outline for Piecewise Function

I. Introduction to Piecewise Functions

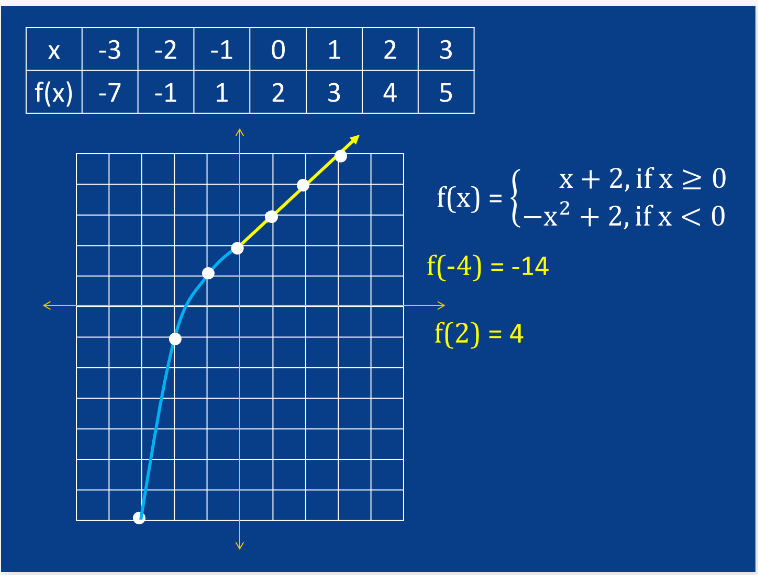
• Definition: A function defined by multiple sub-functions, each applying to a specific interval of the domain.

• Importance: Useful for modeling real-world situations where behavior changes at certain points.

II. Components of a Piecewise Function

• Sub-functions: Different expressions that define the function in various intervals.

• Intervals: The specific ranges of the independent variable (usually x) for which each sub-function applies.

• Conditions: Criteria that determine which sub-function to use based on the input value.

IV. Graphing Piecewise Functions

• Steps to graph:

  1. Identify the intervals and corresponding expressions.

  2. Graph each sub-function within its defined interval.

  3. Use open or closed dots to indicate whether endpoints are included.

• Example: Visual representation of the function defined above.

V. Evaluating Piecewise Functions

• Process:

  1. Determine which interval the input value falls into.

  2. Apply the corresponding expression to find the output.

• Example: Evaluate f(1) and f(-3) for the above function.

VI. Applications of Piecewise Functions

• Real-world examples:

  • Tax brackets (different rates for different income ranges)

  • Shipping costs (varying rates based on weight)

  • Physics (different equations for different phases of motion)

VII. Conclusion

• Summary of key points: Definition, components, notation, graphing, evaluation, and applications.

• Importance of understanding piecewise functions in mathematics and real-life scenarios.

Outline: The Inverse of a Function

I. Introduction to Inverse Functions

• Definition of an inverse function

• Notation: If ( f(x) ) is a function, its inverse is denoted as ( f^{-1}(x) )

• Importance of inverse functions in mathematics

II. Conditions for Inverses

• A function must be one-to-one (bijective) to have an inverse

  • Definition of one-to-one functions

  • Horizontal line test for one-to-one functions

III. Finding the Inverse of a Function

• Steps to find the inverse:

  1. Replace ( f(x) ) with ( y )

  2. Swap ( x ) and ( y )

  3. Solve for ( y )

  4. Replace ( y ) with ( f^{-1}(x) )

Example:

• Given ( f(x) = 3x - 2 )

  • Step 1: wrote y = f(x)

  • Step 2: solve the equation for x: x= y+2/3

  • Step 3: interexchange x and y: y= x+2/3

  • Step 4: therefore, the inverse function is: f-1(x) = x+2/3

IV. Graphing Inverse Functions

• Relationship between a function and its inverse on a graph

  • Reflection over the line ( y = x )

• Example of graphing a function and its inverse

V. Properties of Inverse Functions

• ( f(f^{-1}(x)) = x ) for all ( x ) in the domain of ( f^{-1} )

• ( f^{-1}(f(x)) = x ) for all ( x ) in the domain of ( f )

• Inverses of common functions:

  • Linear functions

  • Quadratic functions (restricted domain)

  • Exponential and logarithmic functions

VI. Applications of Inverse Functions

• Solving equations

• Real-world applications (e.g., physics, economics)

• Importance in calculus (e.g., integration and differentiation)

• Summary of key points

• Importance of understanding inverse functions in mathematics