Unit 9

Formulas

• Work done in moving a charge in an electric field - W=\Delta V volts

• Electric potential - V=\frac{U}{q} volts

• Change in electric potential - \Delta V=\frac{\Delta U}{q} volts

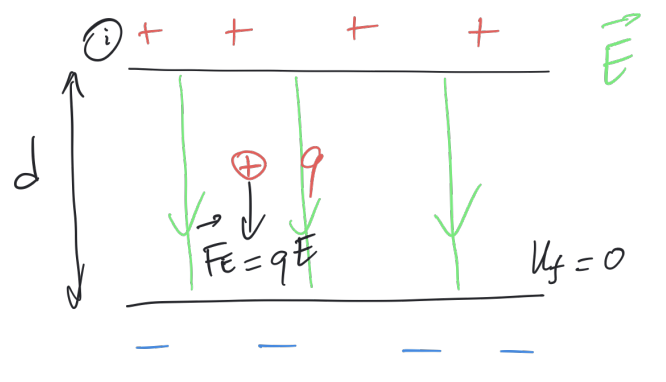
• Electric potential energy: U = qEd joules

• Electric force on a charge in a field: F_E = qE Newtons

• Electric potential for any field: U = qV joules

• Electric potential for a uniform electric field: U=qEd joules

• Conservation of energy - Ki+Ui=Kf+Uf

• Kinetic energy - \frac{mv^2}{2}

Units

• Volts (V) - 1 Joule per Coulomb (1 V = 1 J/C)

General Notes

• When you have a conservative force in an electric field, it always points in the direction of decreasing potential energy

• As a particle moves in the direction of the electric field, the electric potential energy for the particle decreases

• Electric potential energy depends on both the charge and the electric potential experienced by that charge

• Potential difference is crucial in analyzing work done in electric systems, as it directly relates to changes in potential energy

• A positively charged particle will accelerate in the direction of the electric field and to a low potential

• A negatively charged particle will accelerate in the opposite direction of the electric field and to a high potential

• Electric Potential - the potential for potential energy within an electric field

• Relationship between F_e and E if q > 0 - parallel

• Relationship between F_e and E if q < 0 - antiparallel