AP Statistics Notes: Unit 5
Random Variables:
Discrete Random Variable: X takes a fixed set of possible values with gaps between them.
Continuous Random Variable: X takes all values in an interval of numbers. The probability distribution of X is described by a density curve. The probability of any event is the area under the density curve and above the values of X that make up the event.
Checking if a distribution is legitimate: all probabilities are more than 0 and less than 1 + all probabilities added up are equal to 1
Calculating Discrete Random Variables:
Check by Graphing Calculator: one-variable stats (List: L1, Frequency: L2)
Mean Formula:
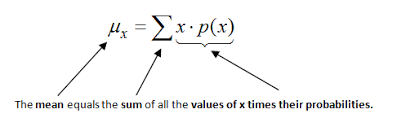
Standard Deviation Formula:

⭐️Variance is before taking the square root of the mean
Transforming and Combining Random Variables:
Finding Probability (Using normal distribution): normalcdf (target range: min and max)
Transforming a Distributions Shape, Center, and Spread:
Addition and Subtraction ONLY changes: measures of center and location (mean, median quartiles, and percentages)
Multiplication and Divison ONLY changes: measures of center, size/scale, and range (example: standard deviation)
Changing Random Variables:
T=Combonation
D=Difference
MeanT Formula: M1+M2=MT
Standard DeviationT Formula: √sx²+sx²
MeanD Formula: M1-M2=MD
Standard DeviationD Formula: √sx²+sx² (yes, it’s just the same thing)
The Distribution of Random Variables:
Binomial distribution summarizes the number of trials, or observations, when each trial has the same probability of attaining one particular value.
Check for a binomial distribution by using: BINS (Binary, Independent, Number, Success)
Binomial Distribution Mean Formula: number x probability = mean (np)
Binomial Distribution Standard Deviation Formula: mean(1-probability)=Sx √(np(1-p))
The 10% rule (checking normal approximation for a binomial distribution): n≤N ✅
Geometric Distribution Mean Formula: 1/probability (1/p)
Geometric Distrubtion Standard Deviation Formula: σ = √((1 - p) / p²)
Probability Guidebook:
normalcdf: probability between two x-values
binomialcdf, and geometcdf: equal to or less than x-value (subtract answer from 1 if looking for equal to or greater than)
normalpdf, binomialpdf, and geometpdf: equal to x-value