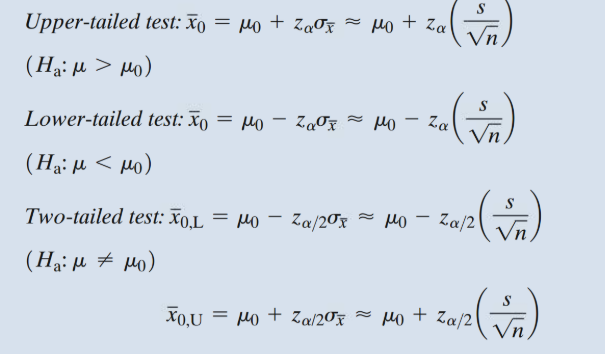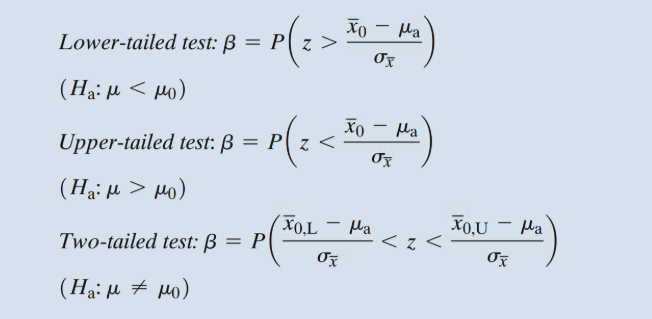Exam 3 - Chapters

Chapter 6

6.1 - Identifying and Estimating the Target Parameter

What is the goal of chapter?
- estimate the value of an unknown population parameter, such as a population mean or a proportion from a binomial population
True or false?
- different techniques are used for estimating a mean or proportion, depending on whether a sample contains a large or small number of measurements
What is the target parameter?
- the population parameter of interest - unknown mean or proportion
- denoted by theta - \theta
Determining the Target Parameter
With quantitative data, you are likely to be estimating the mean or variance of the data
With qualitative data, specifically with two outcomes, the binomial proportion of successes is likely to be the parameter of interest.
What is the point estimator?
- formula definition: a rule or formula that tells us how to use the sample data to calculate a single number that can be used as an estimate of the target parameter
- a single number calculated from the sample that estimates a target population parameter
  - ex: using the sample mean, x̄, to estimate the population mean \mu, thus x̄ is the point estimator
What can be used to attach a measure of reliability to an estimate?
- obtaining an interval estimator - a range of numbers that contain the target parameter with a high degree of confidence
- formula definition: an interval estimator - a formula that tells us how to use the sample data to calculate an interval that estimates the target parameter
What is another term for interval estimator?
- a confidence interval

6.2 - Confidence Interval for a Population Mean: Normal (z) Statistics

According to the CLT, the sampling distribution of the sample mean is approximately normal for large samples
- x̄\pm1.96\sigma_{x̄}=x̄\pm1.96\left(\frac{\sigma}{\sqrt{n}}\right)
If n\ge30, CLT and the normal (z) statistics can be used to determine the form of the sampling distribution of x̄
We are not certain that a true mean exists in an interval, but we can be confident if it is in the interval x̄\pm1.96\sigma_{x̄}=x̄\pm1.96\left(\frac{\sigma}{\sqrt{n}}\right)
- 95% sure that the interval contains \mu
- confidence coefficient: .95
- confidence level: 95%
What is the confidence coefficient?
- the probability that a randomly selected confidence interval encloses the population parameter
What is the confidence level?
- confidence coefficient as a percentage
If our confidence level is 95%, then in the long run, 95% of our confidence intervals will contain \mu and 5% will not
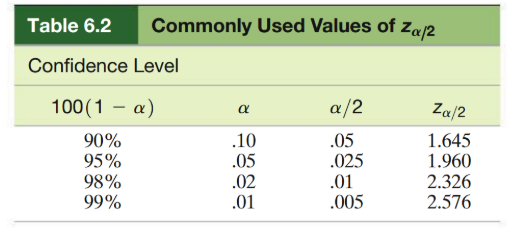
If you choose a confidence coefficient instead of .95,like .99, the confidence coefficient .99 - .01, the .01 is alpha and split between the tail ends. \frac{\alpha}{2}
(1-\alpha) = x̄\pm\left(\frac{\left(Z_{\alpha}\right)}{2}\right)\sigma_{x̄}
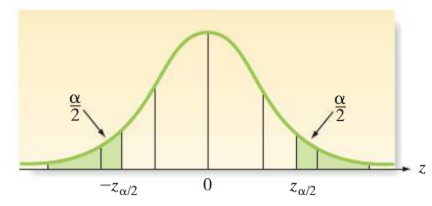
The value \alpha=P\left(Z>Z_{\alpha}\right)
- Z_{\alpha} is the value of the standard normal random variable - z such that the area \alpha will lie to its right
Commonly Used Values
Confidence Intervals are preferred to point estimators, as they have more reliability

6.3 - Confidence Interval for a Population Mean: Student’s t-statistic

What are the two issues with usage of a small sample in making an inference about \mu ?
- The shape of the sampling distribution is no longer assumed normal by CLT
  - solution: as long as the sampled population is normal, the sampling distribution is as well
- The population standard deviation \sigma is almost always unknown.
  - so, instead of using z-score, we use the t-statistic
  - t=\frac{x̄-\mu}{\frac{s}{\sqrt{n}}}
The actual amount of variability in the sampling distribution of t depends on the sample size n, so to express this we say t-statistic has (n-1) degrees of freedom (df).
- the smaller the number of degrees of freedom associated with the t-statistic, the more variable will be its sampling distribution
The t-value increases as the df decreases

What are the conditions required for a valid small-sample confidence interval for \mu?
- A random sample is selected from the target population
- The population has a relative frequency distribution that is approximately normal

6.4 - Large-Sample Confidence Interval for a Population Proportion

What are the properties of the sampling distribution of \^{p} ?
- The mean of the sampling distribution is p
- The standard deviation of \^{p} is \sqrt{\frac{pq}{n}}
  - \sigma_{\^{p}} = \sqrt{\frac{pq}{n}}
  - q = 1-p
- For large sample, the sampling distribution of \^{p} is approximately normal, as long as n\^{p}\ge15 and n\^{q}\ge15
Formula for Large-Sample CI for \^{p}?
- \^{p}\pm Z_{\frac{\alpha}{2}}\sqrt{}\frac{pq}{n}
What conditions are required for a valid large-sample CI for p?
- a random sample is selected from the target population
- the sample size n is large
  - np > 15
  - nq > 15
What is the Wilson CI for a population proportion?
- p̃\pm z_{\frac{\alpha}{2}}\sqrt{\frac{p\left(̃1-p̃\right)}{n+4}}
  - use with extremely large sample size

6.5 - Determining the Sample Size

Estimating a Population Mean
- To estimate a population mean, z_{\frac{\alpha}{2}}\left(\frac{\sigma}{\sqrt{n}}\right)=SE
  then, n = \left\lbrack\frac{\left(z_{\frac{\alpha}{2}}\right)\sigma}{SE}\right\rbrack^2
- Find standard deviation by using s or R/4
Estimating a Population Proportion
- To find the sampling error,
  - z_{\frac{\alpha}{2}}\sqrt{\frac{pq}{n}}=SE
  - then, n = \frac{\left(z_{\frac{\alpha}{2}}\right)^2\left)\left(pq\right)\right.}{\left(SE\right)^2}

6.6 - Simple Random Sampling

Finite Population Correction for Simple Random Sampling
- What is the simple random sampling with finite population of size N?
  - Estimation of the Population Mean
  - Estimated standard error:
    - \sigma_{(x̄)}=\frac{s}{\sqrt{n}}\sqrt{\left(\frac{N-n}{N}\right)}
      - approximate 95% CI x̄\pm2\sigma_{x̄}
  - Estimation of Population Proportion
  - Estimated standard error:
    - \sigma_{p̂}=\sqrt{\left(\frac{p̂\left(1-p̂\right)}{n}\right)}\sqrt{\frac{N-n}{N}}
      - approximate 95% CI p̂\pm2\sigma_{p̂}

6.7 - Confidence Interval for a Population Variance

What is the 100(1-\alpha) Confidence Interval for \sigma^2
- \frac{\left(n-1\right)s^2}{X^2\frac{\alpha}{2}}\le\sigma^2\le\frac{\left(n-1\right)s^2}{x^2\left(1-\frac{\alpha}{2}\right)}
What are the conditions required for a valid CI for \sigma^2?
- a random sample is selected from the target population
- the population of interest has a relative frequency distribution that is approximately normal

Chapter 7

7.1 - The Elements of a Test of Hypothesis

What is a statistical hypothesis?
- a statement about the numerical value of a population parameter
What are the two hypotheses?
- null hypothesis: represents the status quo to the party performing the sampling experiment
- alternative/research hypothesis: which will be accepted only if the data provide convincing evidence of its truth
H_0=,\ge,\le
H_{a}\ne,<,>
The null hypothesis has to be proven false
The alternative hypothesis has to be proven to be true
If the population size is not large enough to use CLT, we have to compute a test statistic to find the hypothesis
- Z=\frac{x̄-\mu}{\sigma_{x̄}}
Test statistic: a sample statistic to decide between the null and alternative hypotheses: decides if rejecting the null hypothesis occurs
What is a Type 1 Error?
- the researcher rejects the null hypothesis in favor of the alternative hypothesis when null hypothesis is actually true. Probability of this occurring is denoted by \alpha
What is the rejection region?
- the set of possible values of the test statistic for which the researcher will reject the null hypothesis in favor of the alternative hypothesis
What is a Type 2 Error?
- the researcher failing to reject (accepts) the null hypothesis when it should be rejected
- denoted by \beta
Conclusions and Consequences for a test of Hypothesis
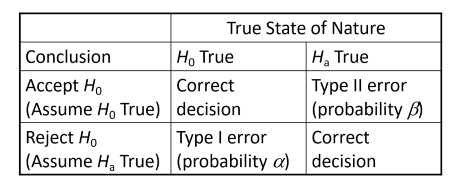
Be careful not to accept H_0, as the measure of reliability = \beta=P\left(TypeII\right) is almost always unknown, so we say fail to reject H_0 instead

7.2 - Formulating Hypotheses and Setting up the Rejection Range

Forms of alternative hypothesis
- One tailed, upper tailed
  - H_{\alpha}:\mu>2,400$
- One tailed, lower tailed
  - H_{\alpha}:\mu<2,400
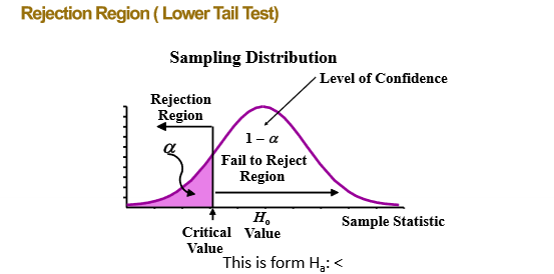
- Two-tailed
  - H_{\alpha}:\mu\ne2,400
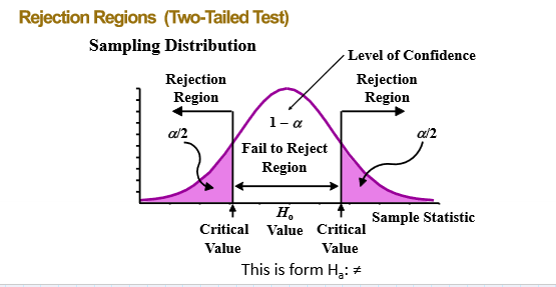
From now on, null hypothesis will always be set to an equal sign
Key Words for upper-tailed:
- greater than, larger, above
Key Words for lower-tailed:
- less than, smaller, below
Key Words for two-tailed:
- not equal to, differs from

7.3 - Observed Significant Levels: p-Values

What is the p-value?
- probability of observing a value of the test statistic that is at least as contradictory to the null hypothesis and supports the alternative hypothesis
If a p-value is upper tailed, take .5 - t-statistic
If a p-value is lower tailed, just use t-statistic
If a p-value is two-tailed, take t-statistic/2

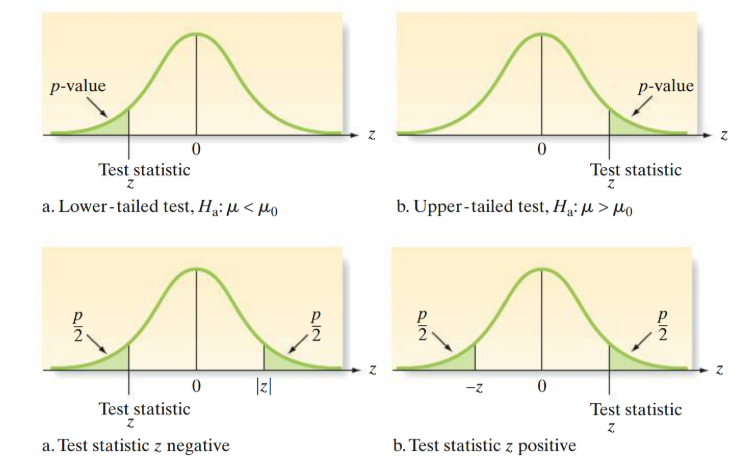
If a p-value is less than alpha, we generally reject the null hypothesis
If a p-value is greater than alpha, we generally fail to reject the null hypothesis

7.4 - Test of Hypothesis About a Population Mean: Normal (z) statistic

The test statistic we use depends on the sample size
- If large, n > 30
- If small, n < 30
- Or if value of population standard deviation is unknown
Large Sample Size
- CLT guarantees that the sampling distribution will be normal, so z-statistic is used.
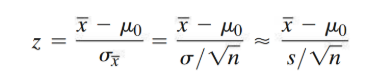
- Conditions Required for a Valid Large-Sample Hypothesis Test

1. A random sample is selected from the target population

2. The sample size n is large (n>30), guaranteeing it will be normal

What are the possible conclusions for a test of hypothesis?
- If the calculated test statistics falls in the rejection region, alpha > p-value, reject Ho and conclude Ha is true.
- If the test statistic does not fall in the rejection region, conclude that the sampling experiment does not provide sufficient evidence to reject Ho at the level of significance

7.5 - Test of Hypothesis About a Population Mean: T-statistic

When a sample is small, we use t-statistic:
- Formula:
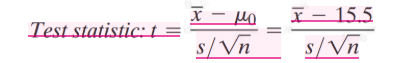
What are the conditions required for a valid small-sample hypothesis test?
- A random sample is selected from the target population
- The population from which the sample is selected has a distribution that is normal
Small-sample inferences typically require more assumptions and provide less information about the population parameter than large-sample inferences.

7.6 - Large-Sample Test of Hypothesis About a Population Parameter

Inferences about population proportions (or percentages) are often made in the context of the probability, p, of “success” for a binomial distribution
What are the conditions required for a valid large-sample hypothesis test for p?
- A random sample is selected from a binomial population
- The sample size n is large enough so that both np > 15 and nq > 15
Sample Samples
- Tests for a population proportion based on the z-statistic may not be valid - especially when conducting one-tailed tests, which is why we use the exact binomial tests for them

7.7 - Test of Hypothesis About a Population Variance

What are the conditions required for a valid hypothesis test for variance?
- A random sample is selected from the target population
- The population from which the sample is selected has a distribution that is approximately normal

7.8 - Calculating Type II Error Probabilities

Steps for Calculating Beta for a Large-Sample Test
- Calculate values of xbar:
- Convert the Xbaro to z-value:
Sketch the alternative distribution and share the area in the nonrejection region and use the z-statistics and Table II to find the B (shaded area)
The power of a test is the probability that the test will correctly lead to the rejection of the null hypothesis.
- Power is equal to (1-B)

Summary of Chapter 7:

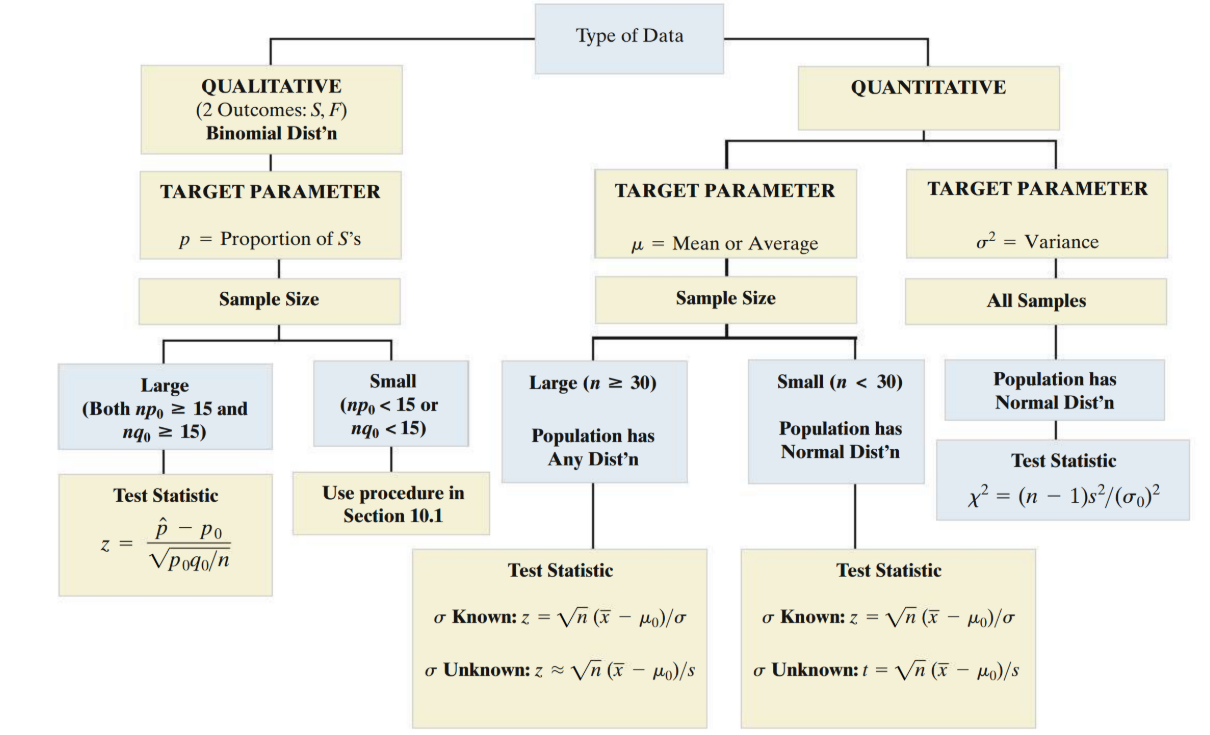
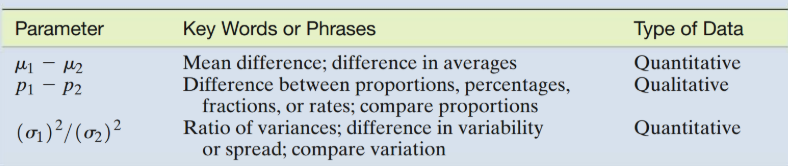
Key words for identifying the target parameter
- μ - mean, average
- p - proportion, fraction, percentage, rate, probability
- σ² - variance, variability, spread
Elements of a Hypothesis Test
- Null Hypothesis (H0): A statement that there is no effect or no difference, used as a starting point for statistical testing.
- Alternative Hypothesis (H1 or Ha): The statement that indicates the presence of an effect or a difference, which researchers aim to support.
- Significance Level (α): The threshold for rejecting the null hypothesis, commonly set at 0.05 or 0.01.
- Test Statistic: A standardized value calculated from sample data during a hypothesis test.
- p-value
- conclusion
Probabilities in Hypothesis Testing
- a = P(Type I Error) = P(reject Ho when Ho is true)
- B = P(Type II Error) = P(accept Ho when Ho is false)
- 1 - B = Power of a Test = P(reject Ho when Ho is false)
Forms of Alternative Hypothesis
- Lower-tailed: Ha: μ < μo
- Upper-tailed: Ha: μ > μo
- Two-tailed: Ha: μ \ne $$ μo
Using p-Values to Make Conclusions
- 1. Choose significance level (a)
- 2. Obtain p-value of the test
- 3. If a > p-value, reject Ho
Guide to selecting a one-sample hypothesis:

Chapter 8

8.1 - Identifying the Target Parameter

Determining the Target Parameter:

8.2 - Comparing Two Population Means: Independent Sampling

In the large-sample case, we use the z-statistic, while in the small-sample case we use the t-statistic
Properties to Know:
Large, Independent Sample Information:

8.3 - Compaing Two Population Means: Paired Difference

Utilizes test statistic for “one sample”

Paired difference experiments are generally more accurate than independent sample experiments
A paired difference experiment is never obtained by pairing the sample observations after the measurements have been acquired