Chapter 11: The Chi-Square Distribution

Introductory

• Three major applications of the chi-square distribution:
    * The goodness-of-fit test, which determines if data fit a particular distribution, such as in the lottery example
    * The test of independence, which determines if events are independent, such as in the movie example
    * The test of a single variance, which tests variability, such as in the coffee example

11.1 Facts About the Chi-Square Distribution

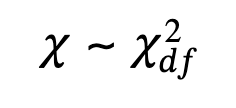
• Degrees of freedom: which depends on how chi-square is being used.
• The population standard deviation is 𝜎=√2(df).
• Population mean: μ = df
• Random variable: X^2
• Squared standard normal variables: χ2 = (Z1)^2 + (Z2)^2 + … + (Zk)^2
    * The curve is nonsymmetrical and skewed to the right.
    * There is a different chi-square curve for each df.
    * The test statistic for any test is always greater than or equal to zero.
    * When df > 90, the chi-square curve approximates the normal distribution.
    * The mean, μ, is located just to the right of the peak

11.2 Goodness-of-Fit Test

• The null and alternative hypotheses for GOF: may be written in sentences or may be stated as equations or inequalities.

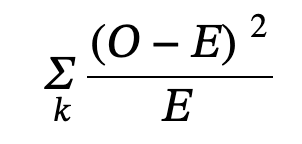
• where
    * O = observed values (data)
    * E = expected values (from theory)
    * k = the number of different data cells or categories
• Null hypothesis: The observed values of the data values and expected values are values you would expect to get.
• Degrees of freedom GOF: Number of categories - 1
• The goodness of fit is usually right-tailed
• Large test statistic: Observed values and corresponding expected values are not close to each other.
• Expected value rule: Needs to be above 5 to be able to use the test

11.3 Test of Independence

• Tests of independence use a contingency table of observed data values

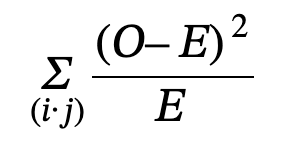
• where
    * O = observed values
    * E = expected values
    * i = the number of rows in the table
    * j = the number of columns in the table
• Test of independence: Determines whether two factors are independent or not
• The null hypothesis for independence: states that the factors are independent
• The alternative hypothesis for independence: states that they are not independent (dependent).
• Independence degrees of freedom: (number of columns -1)(number of rows - 1)
• Expected value formula: (row total)(column total) / total number surveyed

11.4 Test for Homogeneity

• Test for Homogeneity: used to draw a conclusion about whether two populations have the same distribution
• Ho: The distributions of the two populations are the same.
• Ha: The distributions of the two populations are not the same.
• The test statistic for Homogeneity: Use a χ2 test statistic. It is computed in the same way as the test for independence.

11.5 Comparison of the Chi-Square Test

• Goodness-of-Fit: decides whether a population with an unknown distribution "fits" a known distribution.
    * Ho for GOF: The population fits the given distribution
    * Ha for GOF: The population does not fit the given distribution.
• Independence: decides whether two variables are independent or dependent. There will be two qualitative variables and a contingency table will be constructed.
    * Ho for Independence: The two variables (factors) are independent.
    * Ha for Independence: The two variables (factors) are dependent.
• Homogeneity: decides if two populations with unknown distributions have the same distribution as each other. There will be a single qualitative survey variable given to two different populations.
    * Ho of Homogeneity: The two populations follow the same distribution.
    * Ha of Homogeneity*:* The two populations have different distributions.

11.6 Test of a Single Variance

• Test of a single variance: assumes that the underlying distribution is normal
• Hypotheses: stated in terms of the population variance

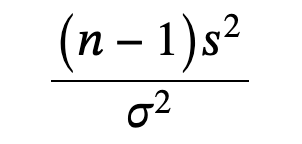
• where
    * n = the total number of data
    * s2 = sample variance
    * σ2 = population variance
• A test of a single variance may be right-tailed, left-tailed, or two-tailed

Examples