PRE-CAL | Parabolas

Definition

• It is the set of all points that are equidistant from a fixed point called the foci and a fixed line called the directrix.

• A parabola devours its focus.

Properties

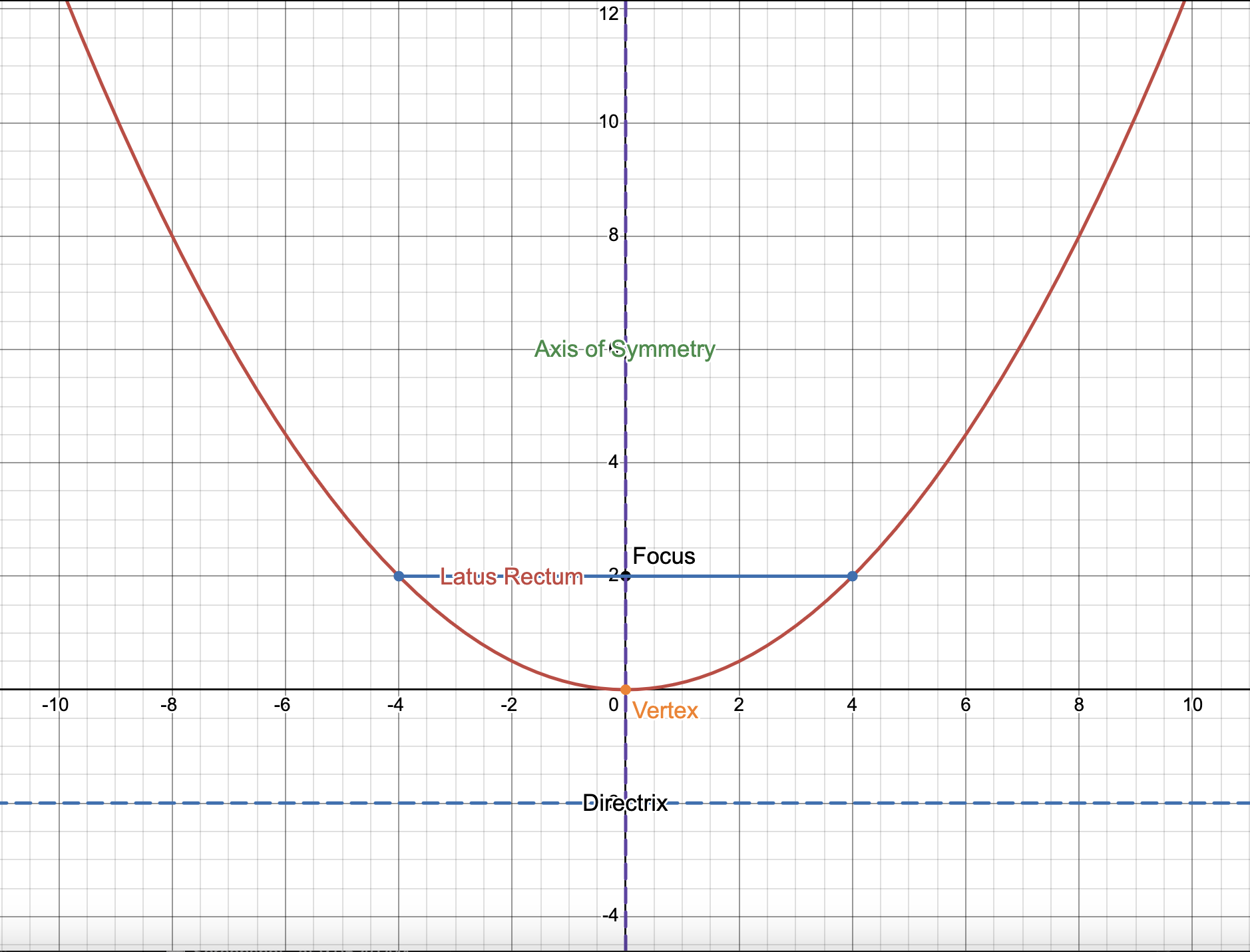
• Focus: the fixed point described in the definition above.

• Directrix: the fixed line that is the point of symmetry of the ellipse.

• Axis of Symmetry: the line that divides the parabola into two equal parts.

• Vertex: The point in the parabola where the direction changes.

• Latus Rectum: the point that passes through the focus and is perpendicular to the axis of symmetry.

• Focal Width: the distance between the vertex and the focus & the distance between the vertex and the directrix

Formula

Variables

• Let p be the focal width.

• Let (h,k) the coordinates of the vertex.

Standard Equation for Parabolas Opening UPWARDS

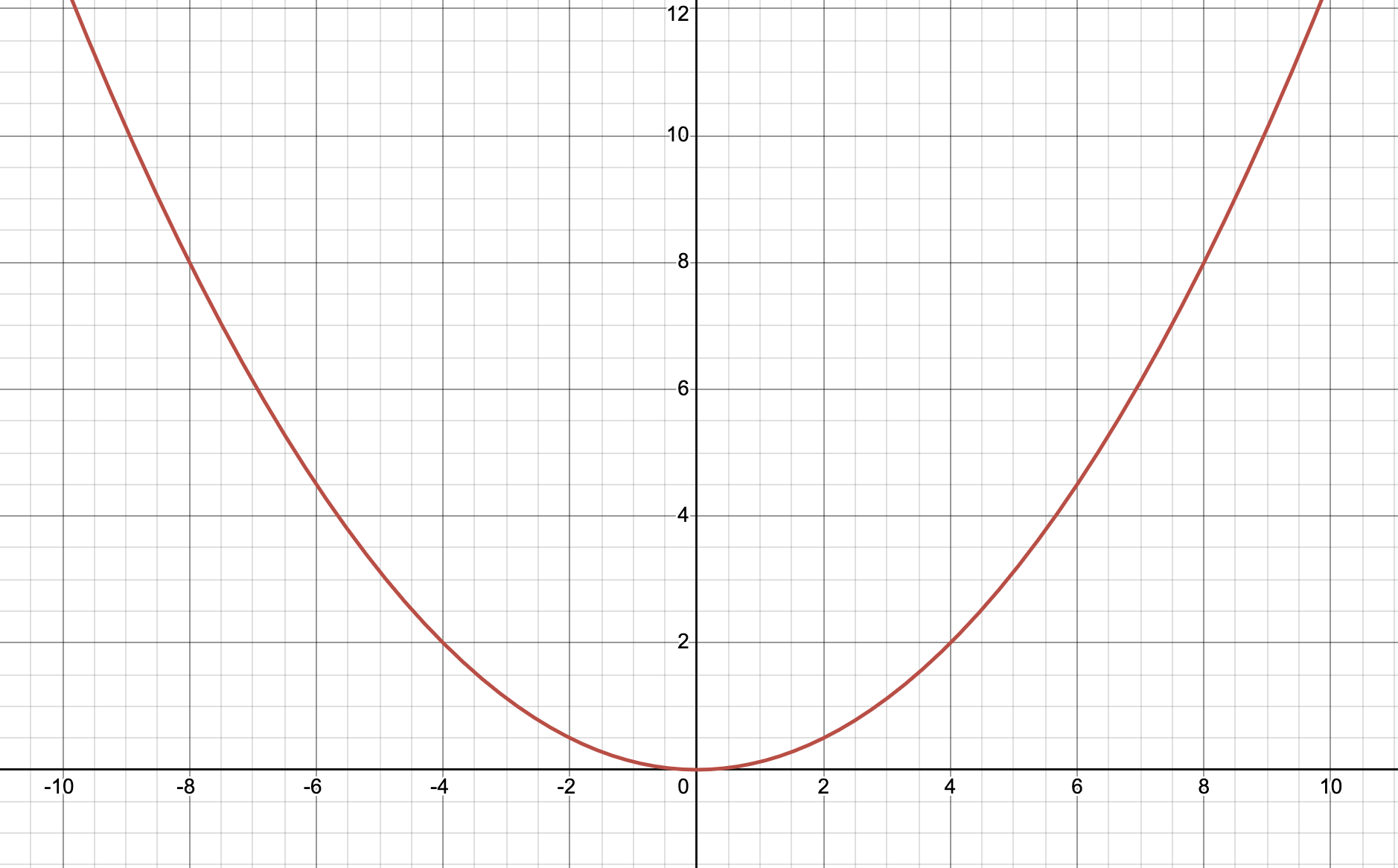
• (x-h)²=4p(y-k)

Standard Equation for Parabolas Opening DOWNWARDS

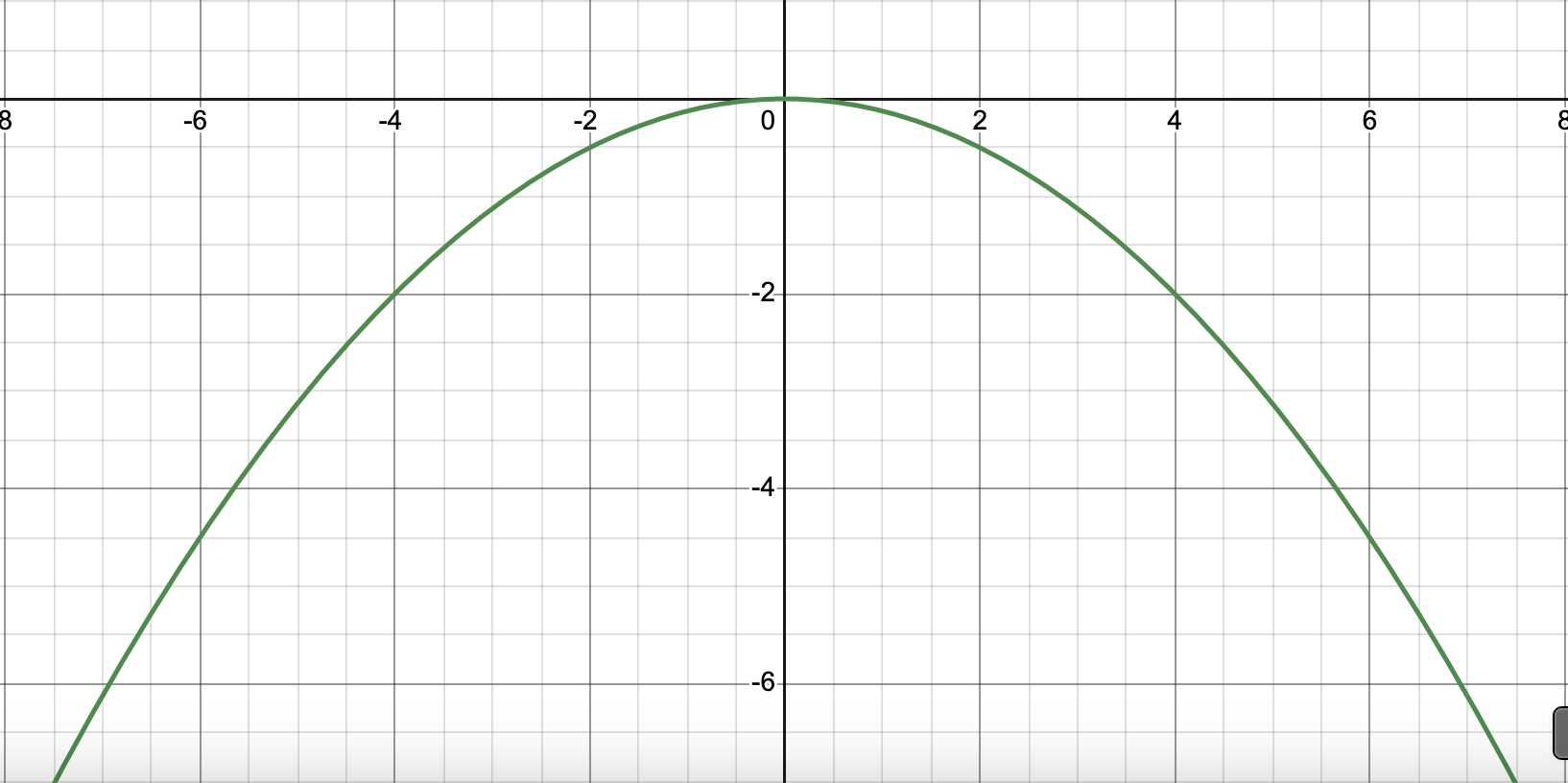
• (x-h)²=-4p(y-k)

Standard Equation for Parabolas Opening TO THE RIGHT

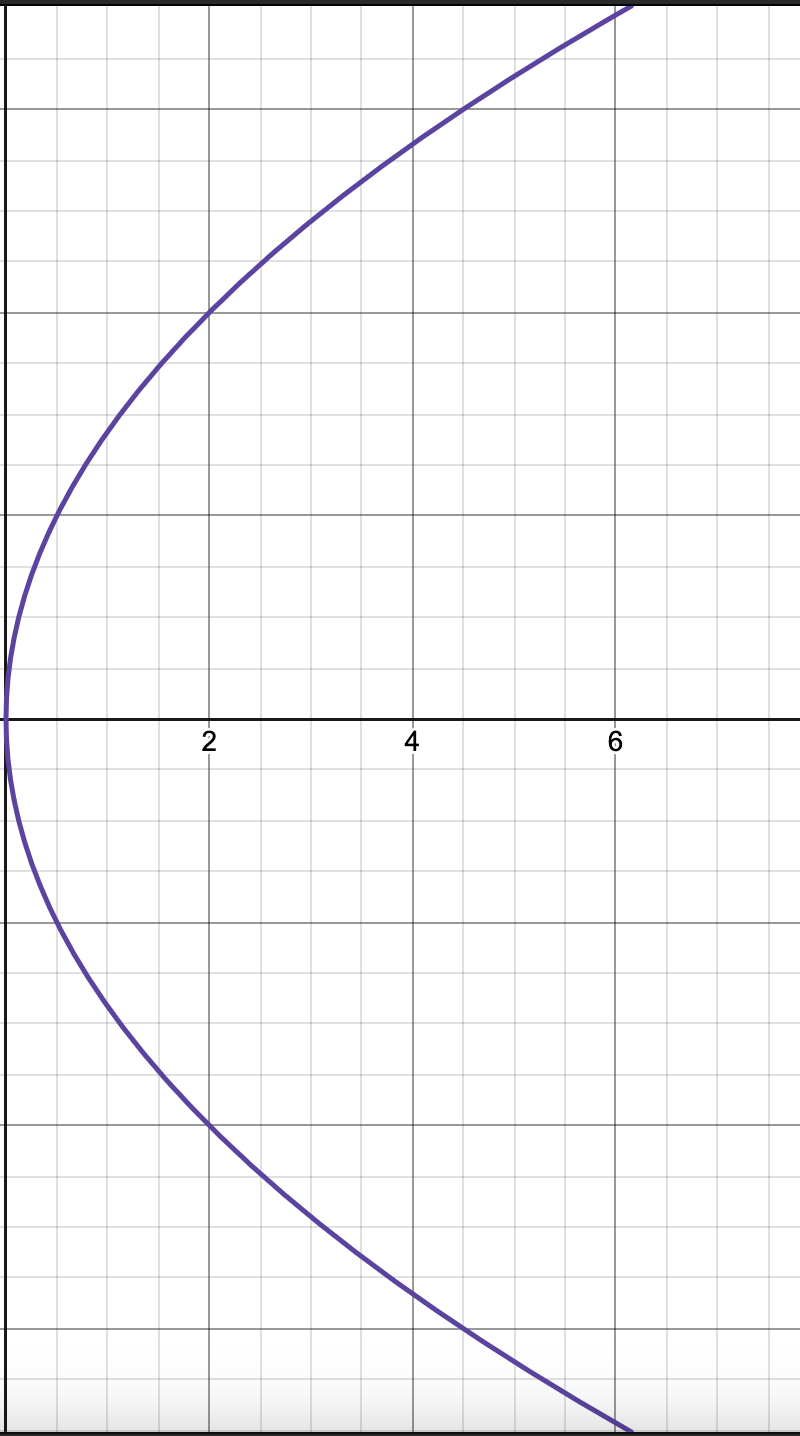
• (y-k)²=4p(x-h)

Standard Equation for Parabolas Opening TO THE RIGHT

• (y-k)²=-4p(x-h)

Graphing a Parabola

1. Identify the vertex of the parabola and graph it based on the constants in the equation.

2. Check how the parabola opens, or its concavity, based on the equation.

3. Solve for p based on the equation.

4. Graph the focus by moving p units from the vertex in the direction the parabola opens.

   • If it opens upwards, graph the focus p units above the vertex.

   • If it opens downwards, graph the focus p units below the vertex.

   • If it opens to the right, graph the focus p units to the right of the vertex.

   • If it opens to the left, graph the focus p units to the left of the vertex.

5. Graph the directrix by moving p units from the vertex in the direction opposite the one the parabola opens.

   • If it opens upwards, graph the horizontal directrix p units below the vertex.

   • If it opens downwards, graph the horizontal directrix p units above the vertex.

   • If it opens to the right, graph the vertical directrix p units to the left of the vertex.

   • If it opens to the left, graph the vertical directrix p units to the right of the vertex.

6. Graph the endpoints of the latus rectum.

   • If it opens upwards or downwards, graph the endpoints 2p units to the left and to the right of the focus.

   • If it opens to the left or to the right, graph the endpoints 2p units below and above the focus.

7. Connect the vertex and the endpoints of the latus rectum in one continuous curved line, ensuring it opens in the right direction and devours the focus.