3.1: Chain Rule

-Composite function- a function inside a function

ex.) 3(x²+2x)²

Chain rule in two steps:

1)Take the derivative of the outside, ignoring the inside

2)Multiply the derivative by what is inside

ex. if differentiating 3(x²+2x)², with the rules of the chain rule, you would get 6(x³+2x)(3x²+2x)

3.2: Implicit Differentiation

x: differentiate like normal

y:differentiate like x

-but after this, we multiply by y’ and use chain room to get it’s derivative.

example problem-3x²-differentiated using the power rule, we get 6x. And if we come acorss 3y² you get 6y. But now you need to multiply gy by 6y’, which will get you the answer 6yy’.

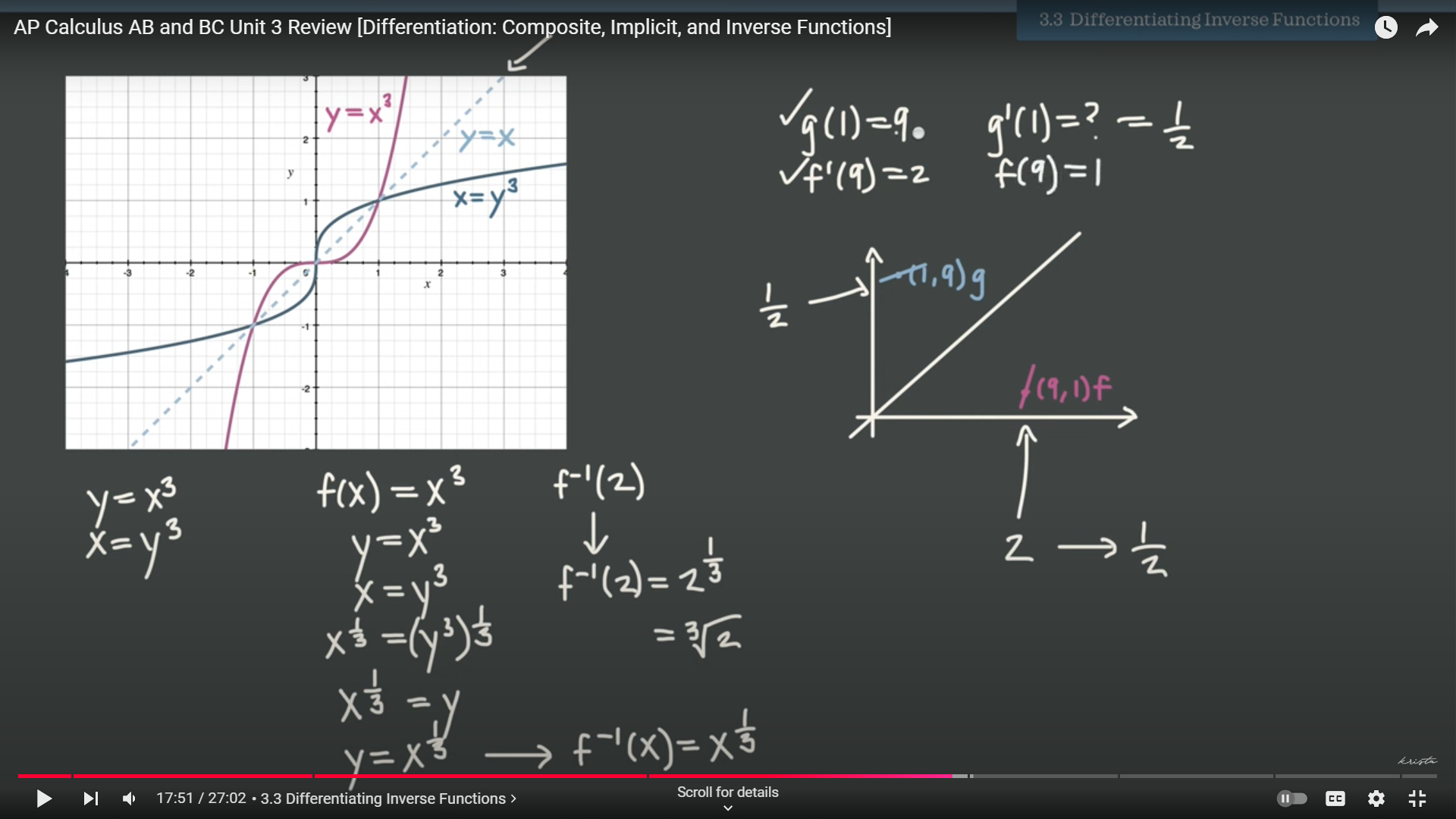
3.3: Differentiating inverse functions