General Chemistry Semester 2 Final Review

highkey the flashcards 4 this are only vocab based so beware

Chapter 9 stoichiometry

SECTION 1

• Composition stoichiometry- deals with the mass relationships of elements n compounds

• Reaction stoichiometry- involves the mass relationships between reactants and products n a chemical reaction

  • Based on chemical equations and the law of conservation of mass

  • All reaction stoichiometry calculations start with a balanced chemical equation. This equation gives the relative numbers of moles of reactants and products

• Problem Type 1: Given and Unknown quantities are amounts in moles

• Problem Type 2: Given is an amount in moles and Unknown is a mass that is often expressed in grams

• Problem Type 3: Given is a mass in grams and unknown is an amount in moles

• Problem Type 4: Given is a mass in grams and unknown is a mass in grams

• Mole ratio- is a conversion factor that relates the amounts in moles of any two substances involved in a chemical reaction

• The molar mass is the conversion factor that relates the mass of a substance to the amount of moles of that substance

• To solve reaction stoichiometry problems, you will need to determine molar masses using the periodic table

SECTION 2

• Balanced equations give amounts of reactants and products under ideal conditions

• Mole-to-gram calculations require two conversion factors 

Amount of given substance (mol) → amount of unknown substance (mol) —> mass of unknown substance (g)

• Multiple the known quantity, by the appropriate conversion factors

• Gram-to-mole conversions require the molar mass of the given substance and the mole ratio

Mass of given substance (g) —> amount of given substance (mol) —-> amount of unknown substance (mol)

• Mass-to-mass calculations use the mole rato and the molar masses of the given and unknown substances

Mass of given substance (g) —> amount of given substance (mol) —> amount of unknown substance (mol) —> mass of unknown substance (g)

SECTION 3

• One reactant limits the product of a reaction

• Limiting reactant- the reactant that limits the amount of the other reactant that can combine and the amount of product that can form in a chemical reaction. 

• Excess reactant- the substance that s not used up completely in a reaction

• Comparing the actual and theoretical yields helps chemists determine the reaction’s efficiency

• Theoretical yield- the maximum amount of product that can be produce from a given amount of reactant

• Actual yield- measured amount of a product obtained from a reaction 

• Percentage yield- the rato of the actual yield to the theoretical yield, multiplied by 100

Percentage yield = actual yield theoretical yield x 100

Chapter 10 states of matter

SECTION 1: THE KINETIC MOLECULAR THEORY OF MATTER

• Scientists developed kinetic molecular theory of matter to understand the behavior or atoms and molecules that make up matter

• Kinetic Molecular Theory (KMT) : Particles of matter are always in motion

• Explains properties of solids, liquids, and gases in terms of energy of particles and forces that act between them

KMT explains the constant motion of gas particles

• Help understand behavior and physical properties of gases

Ideal gas: model provided by the theory; a hypothetical gas that perfectly fits all the assumptions of the KMT

Assumptions of the KMT:

1. Gases consist of large # of tiny particles that are far apart relative to their size

• For the same number of particles, the ones of gases will occupy a volume that is 1000x greater than the volume in liquid or solid state

• This is because molecules of gases are further apart

• Volume occupied by a gas is empty space —> This is why gases have a lower density than liquids and solids

• Makes gases to be easily compressed

2. Collisions between gas particles and between particles and container walls are elastic collisions 

• Elastic Collision: No net loss of total KE

• KE is transferred between two particles during collisions  and will remain the same as long as the temperature is constant

• Collisions happen when gas particles travel in a straight line and collide each other or container walls

3. Gas particles are in continuous, rapid, random motion, therefore they possess KE

• Gas particles move in all directions

• KE of particles overcomes the attractive forces between them, except near the temperature at which gas condenses and becomes a liquid 

4. No forces of attraction between gas particles 

• Similar to billiard balls, when gas molecules collide, they will bounce apart instead of sticking together 

5. Temperature of a gas depends on the average KE of the gas particle 

• KE of particle is given by the equation: KE = ½ mv²

• m = mass of particle, v = speed of particle 

• All particles of a specific gas have the same mass, their KE depend only on their speeds

• If temperature increases, the average speeds and KE of gas particles increase and vice versa

• Gases at same temperature have same average KE

• At the same temperature, particles of lighter gas, such as hydrogen, will have higher speeds than heavier gas, such as oxygen

The KMT explains the physical properties of gases

• Applies only to ideal gases

• Do not actually exist but gases behave nearly ideally if pressure is not very high and temperature is not very low

Physical properties of gases:

1. Expansion

• No definite shape or volume

• Completely fill any container they are enclosed and take its shape

• Gas can expand to fill anything that has a  larger volume 

• These facts can be explained by the KMT: gas particles move rapidly in all directions (assumption 3), with no attraction between them (assumption 4)

2. Fluidity 

• Gas particles glide easily past one another because of no attractive forces (assumption 4)

• The ability to flow makes both has gas and liquid to be considered as fluids 

3. Low Density 

• The density of a substance in gaseous state at atm is 1/1000 the density of it in liquid of solid state

• This is because the particles are so much farther apart in the gaseous state (assumption 1) 

4. Compressibility 

• During compression, gas particles are brought closer together (initially very far apart)

• Volume will decrease

• When containers are full of under pressured gas, they can contain more than 100x as many particles of gas as the same size unpressurized containers could contain 

5. Diffusion and Effusion 

• Even without even stirred, gases can spread out and mix with one another 

• Ex: If the stopper of a container of ammonia is removed, ammonia gas will mix up and spread out with the air in the room 

• Random and continuous motion of gas molecules (assumption 3) will carry them throughout space 

• This is called diffusion: Spontaneous mixing of particles of two substances by their random motion (spread out)

• Gases diffuse readily into each other and mix together due to the rapid motion and empty space between molecules 

• Ex: If two different gases are in two separate flasks, they will keep moving in their own flasks as long as the stopcock is closed

• But once you open the stopcock, molecules from both gases will diffuse continuously back and forth through the stopcock opening 

• Effusion: Gas particles pass through a tiny opening 

•  Rate of effusion is directly proportional to the velocity  —> Molecules of low mass effuse faster than molecules of high mass

Real gases do not behave according to the KMT

• Particles of real gases occupy space and exert attractive forces on each other 

• Real gas: A gas that doesn’t behave completely according to the assumptions of KMT

• When does a gas not behave like an ideal gas? When pressures are high and temperatures are low, gas particles will be closer together and their KE will be insufficient to overcome the attractive forces 

• Ex: In a car engine cylinder, gas molecules will expand to fill the cylinder, but when you exert pressure on them, they will move closer and reduce the volume

• KMT is more true for gases whose particles have little attraction (weak intermolecular force)

• Noble gases show ideal gas behavior over a wide range of temperatures and pressures, therefore particles of these gases are monatomic and nonpolar 

• No real gas perfectly matches the behavior of an ideal gas

• But under specific conditions like low pressure and high temperature, the behavior of these gases will be very close to that of an ideal gas

• The more polar the gas molecules are (such as NH₃), the greater the attractive forces and the more different the gas will be from ideal gas behavior 

• Nonpolar gases won’t deviate as much from ideal behavior 

• Nonpolar monatomic gas will deviate less from ideal gas behavior compared to a nonpolar diatomic gas (weaker intermolecular forces due to simpler structure and smaller size) —> the simpler/smaller the molecules are, the more similar they behave to an ideal gas

SECTION 2: LIQUIDS

The Intermolecular forces of liquids determine their properties

• A liquid can be described as a form of matter that has a definite volume and takes the shape of its container

• Properties of liquids can be understood by applying the kinetic-molecular theory. 

• Particles in a liquid are in constant motion

  • Particles in a liquid are closer together than the particles in a gas are

    • Particles in a liquid are more effective than those between particles in a gas

    • Example of these forces are dipole-dipole, london dispersion, and hydrogen bonding

• Liquids are more ordered than gases because of stronger intermolecular forces and the lower mobility of the liquid particles 

  • Particles are not bound together in fixed positions but move about constantly

• Fluid- a substance that can flow and therefore take the shape of its container 

Relatively High Density

• Most substances are only slight less dense in a liquid state than in a solid state

  • Water is one of the few substances that becomes less dense when it solidifies

• At the same temperature and pressure, different liquids can differ greatly in density

Relative Incompressibility

• When a liquid is compressed, usually its volume will decrease

  • In contrast a gas under pressure would have only about 1/1000 of its volume at normal atmospheric pressure. 

• Liquids are much less compressible than gases because liquid particles are more closely packed together.  Like gases, liquids can transmit pressure equally in all directions

Ability to Diffuse

• Gases diffuse and mix with other gas particles

• Liquids also diffuse and mix with other liquids

  • Any liquid gradually diffuses throughout any other liquid in which it can dissolve

• The constant, random motion of particles causes diffusion in liquids, as it does in gases

• Diffusion is much slower in liquids than in gases because liquid particles are closer together. 

  • The attractive forces between the particles of a liquid slow their movement

    • As the temperature of a liquid is increased, the diffusion occurs more rapidly

    • Reason is average kinetic energy, and therefore the average speed of the particles, is increased

Surface Tension

• Surface Tension- a property common to all liquids, a force that tends to pull adjacent parts of a liquid’s surface together, thereby decreasing surface area to the smallest possible size

  • Results from the attractive forces between particles of a liquid

  • The higher the force of attraction, the higher the surface tension (VARIES DIRECTLY)

• Water has a higher surface tension than most liquids

  • Due to the large part of the hydrogen bonds water molecules can form with each other

  • Molecules at the surface of the water are a special case

  • They form hydrogen bonds with other water molecules beneath them and beside them, but not with the molecules in the air above them

    • Surface water molecules get drawn together and toward the body of the liquid, creating a high surface tension

  • Surface tension causes liquid droplets to take on a spherical shape because a sphere has the smallest possible surface area for a given volume

• Capillary Action- the attraction of the surface of a liquid to the surface of a solid, is a properly closely related to surface tension

• A liquid will rise quite high in a very narrow tube and will wet the tube if a strong attraction exists between the liquid molecules and the molecules that make up the surface of the tube

  • Attraction tends to pull the liquid molecules upward along the surface and against the pull of gravity 

  • Process continues until the attractive forces between the liquid molecules and the surface of the tube are balanced by the weight of the liquid

• The same process is responsible for the concave liquid surface, called a meniscus, that forms in a test tube or graduated cylinder

Evaporation and Boiling

Vaporization- the process by which a liquid or solid changes to a gas

Evaporation- the process by which particles escape from the surface of a non boiling liquid and enter the gas state

• Evaporation occurs because the particles of a liquid have different kinetic energies

• Particles with higher-than-average energies move faster

• Some surface particles with higher-than-average energies can overcome the intermolecular forces that bind them  to the liquid

• Evaporation is a crucial process in nature

• Boiling is the change of a liquid to bubbles of vapor that appear throughout the liquid

  • Boiling differs from evaporation

Formation of Solids

• When a liquid is cooled, the average energy of its particles decreases 

  • If the energy is low enough, attractive forces pull the particles into an even more orderly arrangement

    • Substance then becomes a solid

• The physical change of a liquid to a solid by remove of energy as heat is called freezing or solidification

SECTION 3: SOLIDS

The particles in a solid hold relatively fixed positions 

• Particles of a solid are more closely packed 

• Intermolecular forces are more effective 

• Interparticle attractive (dipole-dipole-, London dispersion, H-bonding) exert stronger effects in solids

• Attractive forces hold particles in relatively fixed positions, with only vibrational movement around fixed points 

• Since motions of particles are restricted, solids are more ordered than liquids and gases

• Ordered level Gas < Liquid < Solid (?)

2 types of solids: 

1. Crystalline solids

• Most solids consist of crystals 

• Crystal: A substance in which particles are arranged in an orderly, geometric, repeating pattern 

2. Amorphous solid

• Noncrystalline solids (such as glass and plastics)

• Particles are arranged randomly 

Definite Shape and Volume

• Can maintain definite shape without a container

• Crystalline solids are geometrically regular (even their fragments have geometric shapes that reflect internal structure)

• Amorphous solids have definite shape but not geometric 

• Ex: Glass can be molded into any shape and if it’s shattered, the fragments can have different irregular shapes

• Volume only changes slightly with a change in temperature or pressure

• Definite volume because their particles are closely packed

• Little empty space that particles can be compressed

• Crystalline solids do not flow since their particles are held relatively in fixed positions 

Definite Melting Point

Melting: Physical change of solid to liquid by addition of energy as heat

Melting point: Temperature at which a solid becomes a liquid

• At this temperature, KE of particles within a solid will overcome the attractive forces holding them together 

• Particles can break out of their positions in crystalline solids, which have definite melting points

• Amorphous solids don’t have definite melting point and therefore have the ability to overflow a range of temperatures

• Amorphous solids are sometimes referred to as supercooled liquids, substances that retain liquid properties even at temperatures that they appear as solids 

• This is because particles in amorphous solids are arranged randomly, similar to particles in a liquid

• However, unlike particles in a true liquid, particles in amorphous solids are not constantly changing their positions

High Density and Incompressibility 

• Substances are most dense in solid state

• Solids are denser than liquids and gases

• This is because the particles in a solid are more closely packed

• What is the least dense solid? Solid hydrogen 

• It’s density is about 1/320 of the densest element, Os (Osmium)

• Less compressible than liquids 

• Solids such as wood and cork, seem compressible but they are not

• This is because they have pores that are filled with air. When these pores are exerted by intense pressure, they will compress but not the solid matter itself

Low Rate of Diffusion 

• Diffusion does occur in solids but not as fast as in liquids 

Crystal particles are arranged in a 3-dimensional lattice

• Crystal Structure: the total 3-dimensional arrangement of particles of a crystal

• Unit Cell:The smallest portion of a crystal lattice that still shows the 3D pattern of the entire lattice

• Crystal Lattice: A coordinate system that represents the arrangement of particles in a crystal

• Contain many unit cells packed together

7 types of symmetry

1. Cubic

2. Tetragonal

3. Hexagonal

4. Trigonal

5. Orthorhombic

6. Monoclinic

7. Triclinic

Enables scientists to use shape to classify crystals

Binding Forces in Crystals

 4 types of crystals

1. Ionic

• Structure: positive & negative ions in a regular pattern (ions can be monatomic & polyatomic)

• Typically form when metals from Group 1 & 2 combine with nonmetals/nonmetallic polyatomic ions in Group 16 & 17

• Qualities: Hard, brittle, high melting points, good insulators, non conductors 

• Why? Strong binding forces between positive and negative ions

2. Covalent Network

• Structure: atoms are covalently bonded to their closest neighbors

• Qualities: Hard, Brittle, high melting points, nonconductors or semiconductors

• Covalent bonding extends throughout networks that include many atoms

• Examples: diamond - Cx, quartz - (SiO2)x, and silicon carbide - (SiC)x

• Typically are oxides of transition metals 

• Examples above are basically giant molecules

**Subscript x shows that the component in the parenthesis extends forever and ever

3. Metallic

• Structure: metal cations surrounded by a sea of delocalized valence electrons

• Qualities: high electrical conductivity

• Electrons are from metal atoms belonging to the whole crystal

4. Covalent Molecular

• Structure : Covalently bonded molecules held by intermolecular forces

• Qualities: Low melting point, easily vaporized, soft, and good insulators

• Nonpolar covalent: weak london dispersion forces between bonds (H2, CH4, C6H6)

• Polar covalent: stronger dispersion forces like dipole-dipole or even H-bonding (H20 & NH3)

forces holding molecules together are weaker than covalent chemical bonds between atoms

The particles in amorphous solids are not arranged in a regular pattern

• Amorphous Solid: “Without shape” atoms are not arranged in a regular pattern

• Examples: glass & plastic

• Glass: made by cooling certain molten materials that prevents crystallization

• Plastic: molded at high temperatures and pressures (used in structural materials)

• Electronic devices: solar cells, copiers, laser printers, flat panels for computer monitors & screens

Emily

SECTION 4: CHANGES OF STATE

Substances in equilibrium change back and forth between states at equal speeds

• Why do some liquid chemical substances (like rubbing alcohol) have an easily detected scent? Molecules at the liquid’s surface have enough energy to evaporate, overcoming the attraction of neighboring molecules

• Phase: Any part of a system that has uniform composition and properties

• Condensation:process by which gas turns into a liquid

• Equilibrium: dynamic condition in which two opposing changes happen at equal rates in a closed system

• If the temperature of a CLOSED liquid stays constant, so will the rate of evaporation

• Example: 

1. In a closed bottle of rubbing alcohol, high energy molecules from the liquid begin to evaporate

2. As evaporation continues as a constant rate, vapor molecules hit the cap of the bottle and begin to condense back into liquid

3. Once the rate of condensation and evaporation are equivalent, equilibrium has been reached

Equilibrium Vapor Pressure of a Liquid

• Equilibrium Vapor Pressure: Pressure exerted by a vapor in equilibrium with its corresponding liquid at a given temperature

• Kinetic Molecular Theory:Temperature increase → increase avg KE of liquid’s molecules → increase # of molecules able to evaporate → increase in molecules in vapor phase → increased equilibrium vapor pressure

• Any substance w=at a given temperature has a specific equilibrium vapor pressure

• Strong attractive forces of liquid = smaller percent of molecules able to evaporate regardless of temperature

• Low percent of evaporation = low equilibrium vapor pressure

• Volatile Liquids: Liquids that are quick to evaporate and have weak forces between particles (ether)

A liquid boils when it has absorbed enough energy to evaporate

• Boiling: conversion of liquid to vapor with the liquid & at the surface

• Boiling Point: temperature at which the equilibrium vapor pressure of the liquid equals the atmospheric pressure

• All energy absorbed is used to evaporate the liquid

• If the temp of the liquid increases, the equilibrium vapor pressure does 2

• Pressure doesn’t change = temperature is constant

• Pressure above the heated liquid increases = temp rises until vapor pressure equals the new pressure & liquid comes to boil once more 

• Vacuum Evaporator: causes boiling at temps that are lower than usual

• Condensed & evaporated milk

• Boils w/o scorching milk or sugars

• Pressure Cooker: cooks food quickly due to its sealed top. The seal builds pressure over the surface of the boiling water inside, increasing the pressure & therefore the temp. 

• Normal boiling point - at 1 atm, 100 degrees celsius

• Energy must be added continuously to keep the liquid boiling

• Added energy doesn’t change liquid’s temperature

• Needed to continue vaporization & is stored in vapor as PE

Molar Enthalpy of Vaporization: amount of heat needed to vaporize 1 mole of liquid at the liquid’s boiling point at constant pressure

• Measures attraction between particles of the liquid

• Stronger liquid molecule’s attraction → increase energy needed → high molar enthalpy of vaporization (MEV)

• Water’s H-bonding causes high MEV & makes it a cooling agent

• Water vapor escaping takes a lot of heat energy away with them

Freezing

• Freezing: physical change of a liquid to a solid

• Liquid→ Solid + heat energy

• Freezing Point: temp at which th solid and liquid are in equilibrium at 1 atm/760 torr/101.3 kPa pressure

• KE: particles of the liquid and solid have the same KE

• PE: energy lost during freezing now stored in liquid

• Decrease in energy → Solid state is more ordered than the liquid state → increase in particle order

• Pure Crystalline Solids

• Melting point and freezing point are the same

• Nomatter atm or outside temperature = ice & liquid water will maintain a temperature of 0 degrees celsius 

• Only after the ice has all melted, the addition of energy will increase the temperature 

• Adding Energy → shifts equilibrium to the right → increases proportion of liquid to ice

A Solid’s Molar Enthalpy of Fusion: amount of energy required to melt 1 mole of solid at the solid’s melting point

• Energy is absorbed → pulls particles apart → solid’s PE increases → decrease in particle order

• Twins with MEV: attraction between solid particles dictates magnitude of the molar enthalpy of fusion

Sublimation and Deposition

• Sublimation: Change of a solid directly to a gas

• Ex: Dry Ice (solid CO2) and Iodine sublime at ordinary temperatures

• Deposition: Gas directly into a solid

• Ex: Formation of frost on a cold surface

Certain conditions warrant water existing in all 3 phases at the same time

• Phase Diagram: Graph of pressure vs temperature that shows the conditions under which the phases of substances exist. Also reveals how the states of a system change with changing temperatures or pressures.

SECTION 5: WATER

The properties of water in all phases are determined by its structure.

• Chemical composition: 2 Hydrogens, 1 Oxygen, connected by polar covalent bonds in both ice and liquid states

• The number of hydrogen bonds between molecules decreases with rising temperature due to increased kinetic energy

• Liquid water: each molecule typically links with 4 to 8 other water molecules, stabilizing its liquid form 

• Nonpolar molecules do not form hydrogen bonds and primarily exist as gases at room temperature

• Ice features a hexagonal molecular arrangement, leading to a lower density compared to liquid water due to the empty spaces between the molecules (this structure is a result of hydrogen bonding)

• Ice melts -> water molecules gain energy, causing them to move closer together, This results in an increase in the density of water compared to ice

• Water molecules are most tightly compacted at approximately 3.98°C (highest density)

• As the temperature rises above this point, the kinetic energy energy of the molecule increases, causing them to move apart and result in a decrease in density 

• Water freezes at 0°C, boils at 100°C (1 atm pressure)

The molar enthalpy of water determines many of its physical characteristics.

• The molar enthalpy of fusion (energy required to melt ice) is 6.009 kJ/mol, while the molar enthalpy of vaporization (energy required to convert water to vapor) is 40.79 kJ/mol 

• Both are relatively high due to the strong hydrogen bonding that must be overcome during these phase changes

• Ice’s ability to float on liquid water is due to its lower density or else it would sink to the bottom of lakes and be less likely to melt

• Both the boiling point and the molar enthalpy of vaporization of water are high compared to those of nonpolar substances of comparable molecular mass

• The values are high because of the strong hydrogen bonding that must be overcome for boiling to occur

• This high molar enthalpy of vaporization makes water useful for household steam heating systems (steams store a great deal of energy as heat) and in living organisms, it helps them resist dehydration

Gases and pressure

Collisions of air molecules generate pressure

• If you pump air into an automobile tire, the pressure in the tire will increase

  • Pressure increase is caused by the increase in the number of collisions of molecules of air with the inside walls of the tire

  • The collisions cause an outward push, or force, against the inside walls.

• Gas molecules exert pressure on any surface with which they collide. 

  • The pressure exerted by a gas depends on volume, temperature, and the number of molecules present

• Pressure (P) is defined as the force per unit area on a surface

Pressure = ForceArea 

Pressure depends on Force and Area

• SI unit for force is the newton, (N)

• The newton is the force that will increase the speed of a one-kilogram mass by one meter per second each second that the force is applied. 

• At Earth’s surface, gravity has an acceleration of 9.8 m/s² 

• Example: A mass of 51 kg exerts a force of 500 N (51 kg x 9.8m/s²) on Earth’s surface. No matter how the dancer stands, she exerts the same force -500 N- against the floor. But the pressure exerted against the floor depends on the area of contact.

Atmospheric Pressure

• The atmosphere, the shell of air surrounding Earth– exerts pressure. 

• The pressure of the atmosphere can be thought of as caused by the weight of the gases that compose the atmosphere.

• Atmospheric pressure is the sum of the individual pressures of the various gases (nitrogen, oxygen, other gases) in the atmosphere

The Barometer

• A barometer is a device used to measure atmospheric pressure

  • First introduced by Evangelista Torricelli

    • Wondered why water pumps could raise water to a maximum height of only about 34 feet

    • Though the height must depend somehow on the weight of water compared with the weight of air. 

    • Reasoned that liquid mercy, about 14 times as dense as water, could be raised only 1/14 as high as water

How a Barometer Works

• The space above the mercury in the tube of a barometer is nearly a vacuum

• The mercury in the tube pushes downward because of gravitational force

• Column of mercury is stopped from falling beyond a certain point because the atmosphere exerts a pressure on the surface of the mercury outside the tube. 

• This pressure is transmitted through the fluid mercury and is exerted upward on the column of mercury

• The exact height of the mercury in the tube depends on the atmospheric pressure, or force per unit area. 

• Pressure is measured in terms of the mercury column’s height in the barometer tube 

• The atmospheric pressure at any given place depends on the elevation and the weather conditions

• If the atmospheric pressure is greater than the average at sea level, the height of the mercury column in a barometer will be greater than 760 mm. (vise versa)

Using a Manometer

• All gases exert pressure

  • Device called a manometer can be used to measure the pressure of an enclosed gas sample

• EX: consider a can filled with air. The atmosphere exerts a pressure on the can. The air inside the can pushes outward and balances the atmosphere’s inward-pushing force. If a vacuum pump removes the air from the can, the outward force is removed, and the atmospheric pressure crushes the can. 

Units of Pressure

• A number of different units are used to measure pressure. 

  • Atmospheric pressure is often measured by a mercury barometer, pressure can be expressed in terms of the height of a mercury column

• Thus the common unit of pressure is millimeters of mercury, symbolized mm Hg. 

• 1 mm Hg is also called 1 torr to honor Torricelli for his invention of the barometer

• The average atmospheric pressure at sea level at O degrees Celsius is 760 mm Hg. 

• One atmosphere of pressure (atm) is defined as being exactly equivalent to 760 mm Hg. 

• In SI, pressure is expressed in derived units called pascals. 

• One Pascal (Pa) is defined as the pressure exerted by a force of one newton (1N) acting on an area of one square meter

  • 1 atm is equal to 1.01325 x 10⁵ Pa, or 101.325kPa

Standard Temperature and Pressure

• To compare gas volumes, one must know the temperature and pressure at which they are measured

• For purposes of comparison, scientists have agreed on standard conditions of 1 atm pressure and 0 degrees celsius

  • These conditions are called standard temperature and pressure, STP

Pascal (Pa) 1 Pa = 1 Nm²

Millimeters of mercury (mm Hg) 

Torr (torr) 1 torr = 1 mm Hg

Atmosphere (atm) 1 atm = 760 mmHg; 760 torr, 1.01325 x 10⁵ Pa, 101.325kPa

Pounds per square inch (psi) 1 psi = 6.89286 x 10³ Pa; 1 atm = 14.700 psi

SINCE THESE ARE EXACT DEFINITIONS OF MEASUREMENT THEY HAVE AN INFINITE NUMBER OF SIG FIGS

EX: P of atmosphere = 0.830 atm

760 mmHg = 1 atm (definition); 101.325 kPa= 1 atm (definition)

1 atm x 760 mm Hg1 atm= mm Hg

1 atm x 101.325 kPa1 atm= kPa

P= 0.830 atm x 760 mm Hg1 atm= 631 mm Hg 

P= 0.830 atm x 101.325 kPa1 atm= 84.1 kPa

The total pressure of a gas mixture is the sum of the pressures of the gases in it

• John Dalton, found that the pressure exerted by each gas in an unreactive mixture is independent of that exerted by other gases present

• The pressure of each gas in a mixture is called the partial pressure of that gas

• Dalton’s law of partial pressures states that the total pressure of a gas mixture is the sum of the partial pressures of the component gases

Dalton’s Law and the Kinetic-Molecular Theory

• Each of the rapidly moving particles of gases in a mixture has an equal chance to collide with the container walls

  • Therefore each gas exerts a pressure independent of that exerted by the other gases present

  • Total pressure is the result of the total number of collisions per unit of wall area in a given time

Vapor Pressure of Water

• Gas produced by the reaction displaces water, which is more dense, in the collection bottle. 

• You need to apply Dalton’s law of partial pressures in calculating the pressures of gases collected in this way

  • A gas collected by water displacement is not pure but always mixed with water vapor

    • Because water molecules at the liquid surface evaporate and mix with the gas molecules

• In a closed system, water vapor, like other gases, exerts a pressure known as vapor pressure 

EX: you wished to determine the total pressure of the gas and water vapor inside a collection bottle. You would raise the bottle until the water levels inside and outside the bottle were the same. At that point, the total pressure inside the bottle would be the same as the atmospheric pressure, Patm from a barometer in the laboratory. Subtract the vapor pressure of the water at the given temperature from the total pressure. The vapor pressure of the water varies with the temperature. 

The Gas Laws

Pham

• Gas Laws: relationships among the volume, temperature, pressure, and amount of a gas

Gas volume and pressure are indirectly proportional 

• Robert Boyle: doubling the pressure of gas at constant temperature = reducing its volume by ½ 

• As pressure increases, volume decreases

• Pressure of gas is caused by moving molecules hitting the container walls

• Suppose the volume of a container decreases, but at the same temperature, the number of molecules stays the same —> More molecules per unit volume

• As a result, number of collisions increases —> Pressure increases

Graphing Boyle’s Law

Boyle’s law: The volume of a fixed mass of gas varies inversely with the pressure at constant temperature

Boy’s law can be expressed as: PV = k

• Since P and V vary inversely, their product remains the same

Inverse relationship between changes of pressure and volume can be expressed as: P₁V₁ =P₂V₂

P₁ and V₁ are the initial conditions while P₂ and V₂ are a different set of conditions 

Gas volume and temperature are directly related 

• If pressure is constant, gases expand when heated 

• When temperature increases, the volume must increase since molecules collide with the walls of container more frequently with stronger force if the pressure is to stay constant

• At higher temperatures, gas molecules move faster

• Charles discovered that all gases expand to the same extent when heated through the same temperature interval 

• At constant pressure and initial temperature of 0 degree C, the volume changes by 1/273 of the original volume for each Celsius degree

•  Ex: Raising temperature from 0 to 1 degree C =increasing gas volume by 1/273

• Same change occurs if a gas is cooled at constant pressure

• Absolute zero : -273.15 degrees C or 0 in the Kelvin schlage 

• K = 273.15 + degree C

Charles’s Law

• Relationship between temperature in K and gas volume 

• Volume of a gas at constant temperature varies directly with the temperature in K

• Expressed as: V = kt or V/T = k

  • T = Temp. in K

  • k = constant 

  • Ratio V/T always = k

• Charle’s law equation can be applied to volume-temperature problems: V₁/T₁ =V₂/T₂

Gas pressure and temperature are directly related 

• Energy and frequency of collisions depend on KE of molecules 

• For a fixed quantity of gas at constant volume, pressure is directly proportional to temperature in Kelvins, which depends directly on avg KE

• For every K of temperature change, the pressure changes by 1/273

• Gay-Lussac’s law: Pressure of a gas at constant volume varies directly with the temp. in K

• Expressed as: P = kt or P/T = k

  • T = temp. in K

  • k = constant; depends on quantity of gas and volume 

  • For a given mass of gas at constant volume, ratio P/T is the same

• Formula: P₁/T₁ = P₂/T₂

Gas, pressure, temperature, and volume are interrelated 

• When a gas undergoes changes in temp, pressure, and volume all at once, we combine all the three laws 

• Combined gas law: Expresses relationship between pressure, volume, and temperature of a fixed amount of gas

• Expressed as: PV/T = k

• Formula: P₁V₁/T₁ = P₂V₂/T₂

  • Indicates two different sets of conditions 

  • T = temp in K

  • Each gas law can be obtained from combined gas law when the proper variable is constant 

    • Boyle’s law: Temp. is constant 

    • Charles’s law: Pressure is constant 

    • Gay-Lussac’s law: Volume is constant 

Gas Volumes and Ideal Gas LAw

Boyle’s Law

• As pressure goes up, volume goes down = INVERSE RELATIONSHIP

• Ex: es you decrease the pressure on a spacesuit, it EXPANDS

1. P1V1=600

2. P2V2=600

3. P1V1=P2V2

Charles's Law

• As temperature increases, volume increases = DIRECT RELATIONSHIP

• At -273 degrees celsius would theoretically 0 volume

1. V1/T1 = K (constant)

2. V2/T2 = K (constant)

3. V1/T1=V2/T2

1. Molecules move more quickly

2. Takes up more space

3. Collides with the wall more frequently

Steps to solving a boyle’s law equation

1. P1V1=P2V2

2. P1 = first pressure you see

3. V1= the first volume you see in the problem

4. P2 = 2nd pressure you see

5. V2= 2nd volume you see

6. ** Note that one of these variables will likely be missing and you’ll have 2 solve for it

7. If you see the volume going up, expect the volume to go down & vice versa

Example:

P1V1=P2V2

P1=720 torr

V1=450 mL

P2=760 torr.

V2=x

720*450=760x

324000=760x

X = 426.3157895

Rounded to 2 sig figs - X = 430

Boyle’s Law/Charles’ Law Worksheet Answers

1. 231 mL 

Gay-Lussac’s Law

• Studied gas volume relationships involving chemical reactions between hydrogen and oxygen

• 2L of H2(g) + 1L of O2(g) → 2L of water vapor

1. Gas reactions display a 2:1:2 volume ratio applicable to any proportions for volume

2. Constant pressure & temperature = volumes expressed as ratios of small whole #s

3. Different from Dalton’s theory that atoms are indivisible as O2 would have had to be split up to create a 2:1:2 volume ratio.

Equal volumes under the same conditions contain equal # of molecules

Avogadro’s Contributions

• Established that there were 2x as many hydrogens than oxygens in H2O

• All elements that are gases near room temperature (except noble gases) are diatomic

• Used coefficients to balance equations

Avogadro’s Law

1. Same volume, temperature, and pressure = equal numbers of molecules

2. Volume varies directly with number of molecules

3. For Avo’s law to work, “k” must be a constant

• Formula: V=kn

** note: “n” indicates the amount of gas

Standard Molar Volume of a Gas: 1 mol/ 22.4 L

• Same volume, temperature, and pressure Does Not = same mass

Diffusion and Effusion

Diffusion - gradual mixing of two or more gases due to their spontaneous, random motion

Effusion - process where the molecules of a gas confined in a container randomly pass through a tiny opening in the container 

Rates of diffusion and effusion depend on the relative velocities of gas molecules 

• Velocity of gas varies inversely with square root of molar mass

• At same temp, lighter molecules move faster than heavier ones

• Average kinetic energy depends on temperature and equals 1/2mv^2

• Two different gases (A and B) at same temperature - ½ MAvA^2 = ½MBvB^2

• Rate of effusion between two different gases at the same conditions (also can be used to find molar mass of unknown gas)  -

Graham’s law of effusion states that the rates of effusion of gases at the same temperature and pressure are inversely proportional to the square roots of their molar masses.

          TYPES OF MIXTURES

Solutions are homogeneous mixtures

• By soluble we mean capable of being dissolved

• A solution is a homogenous mixture of two or more substances uniformly dispersed throughout a single phase

Components of Solutions

• In a solution, atoms, molecules, or ions are thoroughly mixed, resulting in a mixture that has the same composition and properties throughout.

• The dissolving medium in a solution is called the solvent

• The substance dissolved in a solution is called the solute.

  • The solute is generally designated as that component of a solution that is of lesser quantity

• In a solution, dissolved solute particles are so small that they cannot be seen

  • Remain mixed with solvent indefinitely as long as the existing conditions remain unchanged

Types of Solutions

• Solutions may exist as gases, liquids, or solids. 

• Many alloys, such as brass, and sterling silver, are solid solutions in which the atoms of two or more metals are uniformly mixed. 

The Particles in a Suspension are Large

• If the particles in a solvent are so large that they settle out unless the mixture is constantly stirred or agitated, the mixture is called a suspension. 

  • Jar of muddy water, if left undisturbed, particles of soil collect on the bottom of the jar

  • Soil particles are denser than the solvent, water. 

• Particles in suspension can be separated from heterogenous mixtures by passing the mixture through a filter

Colloids have Particles of Intermediate Size

• Particles that are intermediate in size between those in solutions and suspensions form mixtures known as colloidal dispersions, or simply colloids

  • After large soil particles settle out of muddy water, the water is still cloudy because colloidal particles remain dispersed in the water

    • If cloudy mixture is poured through a filter, the colloidal particles will pass through the filter, and the mixture will remain cloudy. 

• Particles in a colloid are small enough to be suspended throughout the solvent by the constant movement of the surrounding molecules.

• Colloidal particles make up the dispersed phase,  and water is the dispersing medium.  

• EX of Colloids: milk, hair spray, and photographic film

• Colloids can be classified according to their dispersed phase and dispersed medium. 

• Different types of colloids have common names you may recognize 

• Emulsion is a liquid in a liquid, like milk

• Clouds and fog, liquids dispersed in gas, are liquid aerosols

  
  

THE SOLUTION PROCESS

PG.394 Answers: hh

Factors that Affect Dissolving Between a Solid Solute and Liquid Solvent

1. Temperature

• Increasing the temperature increases dissolution. An increase in temperature means an increase in kinetic energy, making the liquid solvent molecules move faster. This makes collisions between solid solute and liquid solvent molecules more frequent, increasing dissolution. 

• Ex: sugar dissolves quicker in hot tea than iced tea because the hot tea (solvent) has more kinetic energy and thus collides with the sugar (solute) more frequently.

• How much temperature affects the solubility of a solid solute in a liquid is UNPREDICTABLE, more unpredictable than temperature’s effect on gas solubility.

• Sometimes it affects the solubility a lot and sometimes very minimally

• KNO3 in water solubility increases drastically with heat

• NaCl in water solubility barely increases with heat

2. Surface Area of Solute

• Ions and molecules of the solute are both attracted to the solvent molecules, causing them to leave the surface on the solid.

• Since dissolution occurs on the face of the solute, the more surface area of the solute means more places for the solute’s molecules to break off of. 

• Ex: powdered sugar dissolves quicker than gradual sugar in water

3. Addition of Agitation

• Mixing, stirring, or shaking the solution disperses the solute particles.

• This makes them more spread out with more opportunities to mingle with the solute.

• Ex: Ur friend group disperses during a party to bag the baddies faster than waiting for them to come up to your group

Solubility: How well one substance dissolves in another

• Limits to the amount of solute that can dissolve in a solvent is dependent on the nature of the solute, nature of the solvent and the temperature.

Unsaturated Solution:  A solution that contains less solute than a saturated solution under the existing conditions

Saturated Solution: A solution that contains the maximum amount of dissolved solute

• Once the dissolution of the solute and recrystallization of the solute reaches equilibrium, it won’t be able to dissolve anymore solute. That solute is just excess now. 

• Ex: finding a perfect friend group makes you comfy. You don’t need anymore friends now.

• Ex: To prepare a saturated solution of sugar in water, one would continuously add sugar into the water until no more sugar is able to be dissolved and sinks to the bottom of the container.

Supersaturated Solution: A solution that contains more dissolved solute than a saturated solution contains under the same conditions

• Ex: To prepare a supersaturated solution of sugar water, take a saturated solution of sugar water and heat it up until the excess sugar dissolves into the water and let it cool devoid of disturbances. 

“Like Dissolves Like”

• Polarity and intermolecular forces affect the formation of ionic compounds. 

• Negatively charged Oxygen in water attracts the positive component of the ionic compound while the positively charged H2 in water attracts the negative component of the ionic compound

• Ex: It’s more effective to use toluene, a nonpolar substance to remove lubricating oil (another nonpolar substance) on your clothing than water (polar). The nonpolar substances will dissolve each other, adhering to the principle that “like dissolves like”.

Hydration: water is the solvent

Hydrates: crystalline compounds that have ratios of water molecules

• Addition of heat to the crystal evaporates the water and leaves an anhydrous salt

• Dissolution in water, water molecules in the crystal leave and join the water as a solute, leaving precipitate at the bottom

• The behavior of a solution made from a hydrate and the behavior of a solution made from the anhydrous salt form is the same

• They both dissolve and create a system with hydrated ions and water molecules

Ionic Compounds

• Typically don’t dissolve in nonpolar solvents since the forces are too weak to attract and separate the ions of the solid

• Differences in bonding, polarity, and intermolecular forces prevent dissolution between 2 substances

Ethanol is pretty lit

• Water is better at dissolving polar and ionic compounds

• Ethanol’s nonpolar region makes it better than water at dissolving less-polar substances

• Ethanol will dissolve in water because of ethanol’s polar -OH component. The polarity of this part of the ethanol molecule allows Hydrogen bonds to form between ethanol molecules and water molecules. On the other hand, carbon tetrachloride will not as it lacks polarity. 

Factors that Affect the Solubility of Gas Solute in a Liquid Solvent

1. Henry’s Law: solubility of a gas in liquid is tethered to the partial pressure of the gas on the surface of the liquid

• This law is applicable when temperature is CONSTANT and only to Gas-Liquid solutions

• If the gas has no reaction, it will dissolve like there aren't any other gases near it. 

2. Pressure

• Increase in pressure increases the solubility of gas. 

• When gas is put under pressure, more of its molecules will dissolve into the liquid. This increase in the amount of solute dissolving will cause the rate of solute escaping to increase as well.

• This forces the equilibrium to be at a higher rate of solubility than before.

3. Temperature

• As temperature increases, the solubility of Gas decreases. 

• Temperature increase causes kinetic energy increase, thus increasing the rate of solvent molecules escaping the surface of the liquid and into the atmosphere. 

• This creates an equilibrium with less gas molecules dissolved in the liquid.

• Ex: If a warm bottle of soda and a cold bottle of soda are opened, the warm bottle will effervesce more because of the increased kinetic energy that comes with the increase in temperature. As time goes on, carbon naturally escapes from the liquid and into the atmosphere in attempts to reach a state of equilibrium. Warming the drink up simply expedites this process. 

Effervescence: the rapid escape of gas from a liquid it was dissolved in

• Ex: opening a can of soda will reduce the pressure back to 1 atm as opposed to 5-10 atm in the unopened can. 

Energy Changes Following Solution Formation

Enthalpy of Solution:the net amount of energy absorbed by a solution when a part of a solute dissolves

• Negative enthalpy of solution = energy release, exothermic reaction (NaOH in water becomes hot)

• Positive enthalpy of solution = energy absorption, endothermic reaction (KI in water becomes cold)

Solvated Molecules: a solute molecule surrounded by solvent molecules

• Ex: When a solute molecule is solvated, energy is being released as the bonds holding the solute molecule together are broken.

CONCENTRATION OF SOLUTIONS

Concentration: The amount of solute in a given amount of solvent

The concentration of solute matters because for example with medications, the wrong concentration of drugs can kill the patient.

• “Dilute” or “concentration” are not definite terms to describe solutions

• “Dilute” - There is a small amount of solute in a solvent

• “Concentrated” - There is a large amount of solute in a solvent

• These terms are unrelated to the degree to which a solution is saturated

Molarity (M) is moles of solute per liter of solution 

• To relate the molarity of the solution to the mass of the solute, you must know the molar mass of the solute

• 1 molar solution of NaOH means that there is one mole of NaOh in every L of the solution

• Ex: 1 mole of NaOh has a mass of 40.0g. If this dissolves in enough water to make exactly 1.00 L of solution, the solution will be a 1 M solution (1 mole/1.00 L)

• Ex: Half a mole of NaOh has a mass of 20.0 g. If this dissolves in enough water to make exactly 1.00 L of solution, a 0.500 M NaOH solution will be produced (.500 mol/1.00L)

• Formula: M = amount of solute (mol) / volume of solution (L)

• Note: 1 M solution is not made by adding 1 mol of solute to 1 L of solvent

• In this case, the final total volume might  not be 1 L

• Instead, 1 mol of solute will first be dissolved in a solvent of less than 1 L

• The solution will then be diluted with more solvent to bring the total volume to 1 L

Molality (m) is moles of solute per kilogram of solvent

“One modal” solution means that 1 mol of solute dissolves in 1 kg of solvent

Ex: 1 mol of NaOh has a molar mass of 40.0 g when it dissolves in 1 kg of water, we will have a one modal NaOH solution (1 mol/1 kg)

Note: If the solvent is in grams, remember to convert it to kilograms using the conversion factor: 1 kg/1000g

• When studying about properties of solutions such as vapor pressure and temperature changes, we use molalities because it is not affected by temperature 

Compounds in Aqueous Solutions

Vocabulary

• Dissociation: Separation of ions when an ionic compound dissolves in water.

• Ionization: Formation of ions from molecular compounds in solution.

• Strong/Weak Electrolyte: Degree to which a compound dissociates in water.

• Net Ionic Equation: Equation showing only the species that actually participate in a reaction.

• Spectator Ions: Ions that do not participate in the chemical reaction.

• Hydronium Ion (H₃O⁺): Common ion formed when acids dissolve in water.

 Main Concepts

Dissociation of Ionic Compounds

• Ionic solids dissociate into individual ions in water.

• Ex:

• NaCl(s) → Na⁺(aq) + Cl⁻(aq)

• CaCl₂(s) → Ca²⁺(aq) + 2Cl⁻(aq)

Calculating Moles of Dissolved Ions

• Use the dissociation equation to find the number of moles of ions.

• Example:
  Al₂(SO₄)₃(s) → 2Al³⁺(aq) + 3SO₄²⁻(aq)
  1 mol Al₂(SO₄)₃ produces 5 moles of ions.

 Solubility and Precipitation Reactions

 Solubility of Ionic Compounds

• Some compounds dissolve in water; others don't.

• Examples:

  • Soluble: NaCl, KNO₃

  • Insoluble: AgCl, CdS

Fig 1.3: Solubility Guidelines

1. All sodium, potassium, and ammonium compounds are soluble.

2. Nitrates, acetates, and chlorates are soluble.

3. Most chlorides are soluble except Ag⁺, Hg₂²⁺, Pb²⁺.

4. Most sulfates are soluble except Ba²⁺, Sr²⁺, Pb²⁺, Ca²⁺.

5. Most carbonates, phosphates, sulfides, and silicates are insoluble (there are exceptions!!).

6. Sulfides of calcium, barium, and magnesium are insoluble.

Precipitation Reactions

• Occur when two soluble salts form a precipitate (insoluble product).

• Example: (NH₄)₂S(aq) + Cd(NO₃)₂(aq) → CdS(s) + 2NH₄NO₃(aq)

Net Ionic Equations

• Shows only ions involved in the chemical change.

• Spectator ions are left out.

• Example: Full ionic:
  Cd²⁺(aq) + 2NO₃⁻(aq) + 2NH₄⁺(aq) + S²⁻(aq) → CdS(s) + 2NO₃⁻(aq) + 2NH₄⁺(aq)
  Net Ionic:
  Cd²⁺(aq) + S²⁻(aq) → CdS(s)

Pg.416-419: Sage

A Molecular Compound Ionizes in a Polar Solvent

• Some molecular compounds can also form ions in solutions (are usually polar compounds)

• Ions are formed from solute molecules by the action of the solvent in a process called ionization

  • Ionization is different from dissociation

  • When an ionic compound dissolves, the ions that were present separate from one another

  • When a molecular compound dissolves and ionizes in a polar solvent, ions are formed where none existed in the undissolved compound

• Ions formed by such a molecular solute are hydrate; like in aqueous solutions

  • Energy is released as heat during hydration of the ions, providing energy needed to break the covalent bonds

• The general extent to which a solute ionizes in solutions depends on the strength of the bonds within the molecules of the solute and the strength of attraction between the solute and solvent molecules

  • If the strength of a bond within the solute molecule is weaker than the attractive forces of the solvent molecules, then the covalent bond of the solute breaks and the molecule is separated into ions

• EX: hydrogen chloride is a molecular compound that ionizes in aqueous solution

  • Contains highly polar bond

  • Attraction between a polar HCl molecule and the polar water molecules is strong enough to break the HCl bond, forming hydrogen ions and chloride ions. 

HCl H+(aq) + Cl-(aq)

The Hydronium Ion

• Many molecular compounds contain a hydrogen atom bonded by a polar covalent bond

  • Some of these compounds ionize in an aqueous solution to release H+

    • The H+ ion attracts other molecules or ions so strongly that it does not normally exist alone

    • Ionization of hydrogen chloride in water is described as chemical reaction in which a proton is transferred directly from HCl to a water molecule

      • Where it becomes covalently bonded to oxygen and forms H3O+

H2O(l)+HCl(g) H3O+(aq)+Cl-(aq)

• The H3O+ion is known as the hydronium ion

  • The reaction of the H+ ion to form the hydronium ion produces much of the energy needed to ionize a molecular solute

An Electrolyte’s strength depends on how many dissolved ions it contains

• Substances that yield ions and conduct an electric current in solution are electrolytes

• Substances that do not yield ions and do not conduct an electric current in solution are non-electrolytes

• Hydrogen Chloride is one of a series of compounds composed of hydrogen and the members of Group 17 (halogens)

• Hydrogen halides are all molecular compounds with single polar-covalent bonds

  • All are gases, soluble in water, and electrolytes

• Hydrogen chloride, hydrogen bromide, and hydrogen iodide strongly conduct an electric current in an aqueous solution

  • Hydrogen fluoride only weakly conducts an electric current at the same concentration

Strong Electrolytes

• Hydrogen chloride, hydrogen bromide, and hydrogen iodide are 100% ionized in dilute aqueous solution

• A strong electrolyte is any compound whose dilute aqueous solutions conduct electricity well; this is due to the presence of all or almost of the dissolved compound in the form of ions.

  • Are all acids in aqueous solution

  • Acids, several other acids, and all soluble ionic compounds are strong electrolytes

• Distinguishing feature of strong electrolytes is to whatever extent they dissolve in water; yield only ions.

  • Example some strong electrolytes, such as NaCl, may be highly soluble in water and form ions in solution

Weak Electrolytes

• Some molecular compounds form aqueous solutions that contain dissolved ions and some dissolved molecules that are not ionized

• Hydrogen fluoride, HF, dissolves in water to give an acidic solution known as hydrofluoric acid

  • hydrogen -fluorine bond is much stronger than the bonds between hydrogen and other halogens

  • When hydrogen fluoride dissolves, some molecules ionize

  • Reverse reaction the transfer of H+ions back to F-ions to form hydrogen fluoride molecules also takes place

HF(aq) + H2O(l) H3O+(aq) + F-(aq)

• Concentration of dissolved intact HF is much greater than the concentration of H3O+ and F- ions

• Hydrogen fluoride is an example of a weak electrolyte

  • A weak electrolyte is any compound whose dilute aqueous solutions conduct electricity poorly; this is due to the presence of a small amount of the dissolved compound in the form of ions. 

• In contrast to a nonelectrolyte, such as the molecular compound sucrose, which dissolves but does not produce any ions in solution

• Another example of weak electrolyte is acetic acid

  • Only a small percentage of acetic acid molecules ionize in aqueous solution

• Description of an electrolyte as strong or weak must not be confused with concentrated or dilute

• Strong and weak electrolytes differ in the degree of ionization or dissociation

  • Concentrated and dilute solutions differ in the amount of solute dissolved in a given quantity of a solvent

Colligative Properties of Solutions

Pg.422-427: Pham

• Colligative properties: Depend on the concentration of solute particles, not the solute’s identity

• The concentration of solute is given in molality

Lower vapor pressure depends on non-electrolyte solute concentration

• The boiling and freezing points of a solution are different from a pure solvent

• Vapor pressure of the solution is lower than that of the pure solvent at the temperature at which the boiling point occurs for the pure solvent

• Solute reduces the freezing point and elevates boiling point 

• Nonvolatile substance: less tendency to become a gas 

• According to equilibrium vapor pressure, at the same temperature, the vapor pressure of a solution containing a nonvolatile solute is lower than that of the pure solvent

• This is because as we have more solute, the amount of solvent (water) decreases. Fewer water molecules will be available to leave the liquid phase, therefore, the tendency to enter the vapor phase decreases compared to pure water

• Equally dilute molal solutions of any nonelectrolyte solutions in the same solvent lower the vapor pressure equally

• Ex: Nonelectrolyte glucose lowers the vapor pressure of water by 5.5 x 10^-4 atm at 25 degrees C in a 1 molal solution 

• This shows how the concentration of non-electrolyte solute particles affects vapor pressure, not its identity

• As the vapor pressure is lowered, the solution will remain as a liquid over a larger range of temperatures by lowering freezing point and raising boiling point 

• Vapor pressure, boiling point, and freezing point are all colligative properties 

A solution with a nonelectrolyte solute will have a lower freezing point that the pure solvent

• Freezing point of a solution with any nonelectrolyte solute is 1.86 degrees C lower than that of water 

• Ex: When 1 mol of nonelectrolyte dissolves in 1 kg of water, the freezing point decreases from 0.00 to -1.86 degrees C

• -1.86 degrees C/m is the molal freezing point constant (K), which is the freezing point depression of the solvent in a 1 molal solution of a nonvolatile, non-electrolyte solute

• Each solvent has its own characteristic molal freezing point constant that is the most accurate at 1 atm

• Freezing-point depression 𝚫t_f: Difference between the freezing points of pure solvent and a solution of a nonelectrolyte in that solvent, directly proportional to the molal concentration 

• Example: Molal concentration doubles = freezing point depression doubles

• Freezing point depression formula: 𝚫t_f = K_fm

• K_f is expressed in degrees C/m

• 𝚫t_f is expressed in degrees C

A solution with a nonelectrolyte solute will have a higher boiling point than the pure solvent

• If the vapor pressure decreases, the boiling point increases

• More energy will be required to raise the vapor pressure of a solution to equal the atmospheric pressure

• Thus, the boiling point of a solution will be higher than the boiling point of pure solvent

• Molal boiling point constant (K_B): the boiling point elevation of the solvent in a 1 molal solution of a nonvolatile, nonelectrolyte solute

• Molal boiling point constant for water is 0.51 degree C/m

• Molal boiling point constants are different for certain solvents

• These values are most accurate for dilute solutions 

• Boiling point elevation 𝚫t_b: difference between boiling points of pure solvent and a nonelectrolyte solution of that solvent; directly proportional to the molal concentration

•  𝚫t_b = K_bm

Pg.428-432 vonese

Osmotic pressure is determined by the concentration of dissolved solute particles.

• Semipermeable membrane (colligative property): allows the passage of some particles while blocking the passage of others.

• By not allowing sucrose molecules to pass through the semipermeable membrane, the rate at which the water molecules move through the membrane and into the solution with sucrose (leaving the pure side) increases

• This causes the level of the solution to rise

• The level keeps rising until the pressure from the height pushes the water back

• The solution stops rising when there an equal rate of water passing through the membrane (equilibrium)

• Osmosis: the movement of solvent through a semipermeable membrane from the side of lower solute concentration to the side of higher solute concentration

  • Occurs when two solutions of different concentrations are separated by semipermeable membrane

• Osmotic pressure: external pressure that muse be applied to stop osmosis

  • Dependent on the concentration of the solute particles, not the type of solute particles which makes it a colligative property 

  • Greater the concentration of solution = greater osmotic pressure of solution

• Regulation of osmosis is vital to the life of a cell because cell membranes are semipermeable

  • Cells lose water and shrink when placed in solution of higher concentration

  • Swell when placed in a solution of lower concentration

  • In vertebrates (animals with a backbone), cells are protected from swelling and shrinking by blood and lymph that surround the cells 

  • Blood and lymph are equal in concentration to the concentration inside cell

The total molality of all dissolved particles determines changes in colligative properties.

• Some substances affect freezing/boiling points more than expected

• Example (with water and freezing points):

  • 0.1 m NaCl lowers FP 2x more than 0.1 m sucrose

  • 0.1 m CaCl2 lowers 3x more

• Sucrose = nonelectrolyte -> 1 mol = DF of 1 (1 mol gives 1 mol of particle)

• NaCl = strong electrolyte -> 1 mol = DF of 2 (Na+ and Cl-)

• CaCl2 -> 1 mol = DF of 3 (Ca2+ and 2Cl-)

• Electrolytes produce more particles, causing greater changes in FP/BP

Actual Values for Electrolyte Solutions (ngl this section’s notes sucks but i had trouble trying to make it comprehensible)

• Values calculated = expected values

• Example:

  • NaCl (2 ions per unit) lowers FP nearly 2x as much as sucrose (nonelectrolyte)

  • Compounds that produce 3 ions per unit lower FP nearly 3x as much as sucrose

• Strong electrolytes behave almost exactly as expected, based on the number of ions they form in a solution 

• Attractive forces between dissociated ions affect their movement in solution

  • The forces are weaker in solution than in solid form but still interfere with ion movement

  • In very dilute solutions, ions move almost freely due to the large distance between them and weaker attraction 

• (Peter)Debye-(Erich)Hückel Theory (1923)

  • Ionic atmosphere: Each ion is surrounded by more ions of opposite charge than like charge

  • Ions form clusters and behave like a single unit, reducing the effective concentration of ions

• High-charge ions attract other ions strongly, so they form stronger clusters and have lower effective concentrations than low-charge ions

441-445: Pham

Properties of Acids and Bases

Acids are identified by their properties

• Acids were first recognized as a distinct class of compounds 

Sour taste 

1. Taste, however, should never be used to evaluate chemicals 

2. Acids, especially in concentrated solutions, are corrosive (destroy body tissues and clothing)

Acids change color of acid-base indicators

3. pH will turn colors in acidic solution when used as an indicator (Ex: Turning red when dipped into vinegar, which shows that vinegar is an acid)

React with active metals and release hydrogen gas

4. Metals above hydrogen in an activity series undergoes single displacement reactions with acids; hydrogen is then formed as a product

5. Ex: Ba_(s) + H₂SO_4(aq) → BaSO_4(s) + H_2(g)

React with bases to form salts and water

6. When chemically equivalent amounts of acids and bases react, three of the properties above disappear because the acid is now neutralized. 

Conduct electric current

7. Acids separate completely into ions in water are strong electrolytes 

8. Others are weak electrolytes

Acid Nomenclature

Binary acid: Contains only two elements: hydrogen and one of the more 

• Many inorganic acids are binary acids

• All hydrogen halides are binary acids

• In pure form, these are gases

Binary Acid Nomenclature 

1. Starts with prefix hydro-

2. The root of the name of the second element follows this prefix

3. Ends with suffix -ic

Oxyacid: An acid that is a compound of hydrogen, oxygen, and a third element, usually a nonmetal

• Although it might seems like the formula shows hydrogen and a polyatomic ion, the hydrogen is actually bonded to oxygen in an oxyacid

• Oxyacids are one class of ternary acids

• Names of anions are based on names of acids

Some acids are useful in industry

1. Sulfuric Acid

   1. Most commonly produced industrial chemical 

   2. Used in petroleum refining, metallurgy, and manufacture of fertilizer 

   3. Essential in production of metals, paper, paint, dyes, detergents, and many chemical raw materials 

   4. Used in automobile batteries

   5. An effective dehydrating agent because it attracts water

   6. Sugar and other organic compounds are dehydrated by sulfuric acid

   7. Can cause serious skin burns 

2. Nitric Acid

   1. Pure nitric acid is a volatile, unstable liquid 

   2. Dissolving in water makes the acid more stable 

   3. Stains proteins yellow (Ex: staining a feather yellow)

   4. Used in making explosives, which are nitrogen containing compounds

   5. Also used in making rubber, plastics, dyes, and pharmaceuticals 

   6. Initially it is colorless but will eventually turn yellow because of decomposition to brown NO₂ gas 

3. Phosphoric acid

   1. Phosphorus is an essential element for plants and animals 

   2. Used for manufacturing fertilizers and animal feed

   3. Sour taste, not toxic

   4. Used as flavoring and cleaning agents

   5. Important in manufacturing detergents and ceramics

4. Hydrochloric acid

   1. Stomach products HCl

   2. Important for pickling iron and steel; pickling is the immersion of metals in acids to remove stains

   3. Used as cleaning agent in industry, in food processing, in activation of oil wells, in recovering of Mg from seawater, and in production of other chemicals 

   4. Concentrated HCl (muriatic acid) can be found in hardware stores

   5. Maintains acidity in pools and cleans masonry 

5. Acetic acid

   1. Pure acetic acid (glacial acetic acid) is a clear, colorless, and pungent-smelling liquid and has a freezing point at 17 degrees Celsius

   2. Forms crystals in cold room

   3. Fermentation of plants produces vinegar that contain acetic acid

   4. White vinegar contains 4-8% acetic acid

   5. Synthesizes chemicals used in manufacture of plastics

   6. Raw material in production of food supplements; ex: lysine 

   7. Also used as a fungicide

Properties of bases differ from acids

1. Bitter Taste

1. Causatic, meaning they attack skin and tissues to cause severe burns

2. Change acid-base indicators blue

1. Sodium Hydroxide (strong base) turns pH paper blue

3. Dilute aqueous solutions of bases feel slippery

1. Soap feels slippery when in contact with water

4. Bases react with acids to produce water and salts

1. Properties of the original base disappear after the addition of equal part acid

5. Bases conduct electricity

1. Bases also form ions in aqueous solutions just like acids. Both acids and bases are electrolytes. 

Arrhenius acids and bases produce ions in solution

1. Aqueous solutions of acids and bases conduct electric current (making them electrolytes

Arrhenius Acid: chemical compound that increases the concentration of hydrogen ions, H+ in aqueous solution

Arrhenius Base: increases the concentration of hydroxide ions, OH- in aqueous solution. 

1. Some bases are Ionic Hydroxides that dissociate in solution to release hydroxide ions.

2. Other bases bond with a hydrogen ion from water, leaving hydroxide ions floating in the solution. 

Aqueous Solutions of Acids

1. Arrhenius definition: molecular compounds with ionizable hydrogen atoms.

2. Water solutions of arrhenius acids are known as aqueous acids and ALL of them are electrolytes.

3. H2O molecules attract 1 or more H+ from acid molecules because acid molecules are sufficiently polar, leaving behind negatively charged anions in the solution.

Strength of Acids

• Acid strength is not dependant on  how many total hydrogen atoms are in the formula, but how many of those actually ionize completely

1. Example: phosphoric acid has 3 hydrogens/1 molecule, but NONE of them ionize completely in solution, making it a weak acid. 

• Strong Acids ionize completely in aqueous solution

1. Strong Acid=Strong Electrolyte

2. Increased acid strength=increased polarity=decreased bond energy

3. Examples of strong acids: perchloric acid (HClO4). Hydrochloric acid (HCl) and nitric acid (HNO3)

• Weak acids ionize partially in aqueous solution & only release few hydrogen ions

1. Aqueous solution of a weak acid contains hydronium ions, anions, and dissolved acid molecules

2. Weak Acid = Weak Electrolyte

3. Decreased acid strength=decreased polarity=increase bond energy

4. Examples of Weak acids: hydrocyanide HCN

5. Ionization reaction and reverse reactions occur simultaneously with weak acids

• Organize acids 

1. Include the carboxyl group

2. Generally weak acids

3. Ex: CH3COOH ionizes slightly in water to give hydronium ions and CH3COO-

• Even though the chemical formula of CH3COOH + water has 4 hydrogens present, only 1 of those four ionizes, making it a weak acid.

• Define acidic hydrogen: the 1 hydrogen/ 4 in CH3COOH that can ionize in H2) to create hydronium

Aqueous Solutions of Bases

• Most bases are ionic compounds that contain metal cations and the hydroxide anion, OH-

• Most bases are ionic and dissociate when dissolved in water 

• Strong Basic Solution: a base completely dissociates to yield aqueous OH-ions.

• NaOH is a common laboratory base because of its water-solubility and complete dissociation

• Note that not all bases are ionic compounds

1. Something like ammonia, NH3, that’s used as a household cleaner is molecular and still a base since it produces OH- ions when reacting with water molecules

Rules based on period:

• All group 1 elements are able to form basic (alkaline) solutions (solutions with a pH over 7)

• Nearly all elements in period D are nearly insoluble in water and don’t produce a large amount of hydroxide ions when added in water, preventing them from producing strongly alkaline (basic) solutions

Alkalinity of Solutions

• Based on how many hydroxide ions are dissolved in the solution, not the total amount of hydroxide ions in the formula

Strength of Bases

• Like Acids, Base strength depends on how much the base dissociates or adds OH- to solution

• Strong Bases are also Strong electrolytes & dissociate fully into OH- and another element in dilute aqueous solutions

• Typically ionic

• Weak Bases are weak electrolytes and don’t dissociate fully in water

• Typically molecular

• Note that many organic compounds that contain Nitrogen, like NH3 are weak bases (like codeine.)

Base/Acid strength table examples

SAGE 452-456:

Acid-Base Theories

Bronsted-Lowry acids and bases donate or accept protons

• Bronsted-Lowry acid- is a molecule or ion that is a proton donor

• Because H+ is a proton, all acids as defined by Arrhenius donate protons to water and are Bronsted-Lowry acids as well

• Substances other than molecules, such as certain ions, can also donate protons

  • Such substances are not arrhenius acids but are included in the category of Bronsted-Lowry acids. 

• Hydrogen chloride acts as a Bronsted-Lowry acid when it reacts with ammonia

  • The HCl transfers protons to NH3 —-> NH4+ + Cl-

• A proton is transferred from the hydrogen chloride molecule, HCl to the ammonia molecule, the ammonium ion, NH4+ is formed. 

• Electron-dot formulas show the similarity of this reaction to the reaction of HCl with water

• In both reactions, hydrogen chloride is a Bronsted-Lowry acid. 

• Water can also act as a Bronsted-Lowry acid

  • Example is the following reaction, in which the water molecule donates a proton to the ammonia molecule

• Bronsted-Lowry base- is a molecule or ion that is a proton acceptor

• In the reaction between hydrocholoric acid and ammonia, ammonia accepts a proton from the hydrochloric acid. It is a Bronsted-Lowry base

• Arrhenius hydroxide bases, such as NaOH, are not, strictly speaking, Bronsted-Lowry bases

  • instead , it is the OH- ion produced in solution that is the Bronsted-Lowry base

    • It is the species that can accept a proton

• Bronsted-Lowry acid-base reaction- protons are transferred from one reactant (the acid) to another (the base) 

  • The figure above shows the reaction between the Bronsted-Lowry acid HCl and the Bronsted-Lowry base NH3

Monoprotic and Polyprotic Acids

• Monoprotic acid- an acid that can donate only one proton (hydrogen ion) per molecule

  • Perchloric acid HClO4, hydrochloric acid, HCl, and nitric acid, HNO3, are all monoprotic 

• The following equations shows how a molecule of the monoprotic acid HCl  donates a proton to a water molecule. 

  • HCl ionizes to form H3O+ ions and Cl- ions. The Cl- has no hydrogens to lose, so HCl has only one ionization step 

HCl (g) + H2O (l) —-----> H3O+ (aq) + Cl-(aq)

• Polyprotic acid- is an acid that can donate more than one proton per molecule

  • Sulfuric acid, H2SO4, and phosphoric acid, H3PO4, are examples of polyprotic acids

    • The ionization of a polyprotic acid occurs in stages

    • Acid loses its hydrogen ions one at a time

• Sulfuric acid ionizes in two sages

  • In its first ionization, sulfuric acid is a strong acid

  • It is completely converted to hydrogen sulfate ions, HSO4-

H2SO4(l)+H2O(l) H3O+(aq)+HSO4-(aq)

• The hydrogen sulfate ion is itself a weak acid. It establishes the following equilibrium in solution

HSO4-(aq)+ H2O(l) H3O+(aq)+SO42-(aq)

• All stages of ionization of a polyprotic acid occur in the same solution

• Sulfuric acid solutions therefore contain H3O+, HSO4-, and SO42- ions. 

  • Note that in sulfuric acid solutions, there are many more hydrogen sulfate and hydronium ions than there are sulfate ions. 

• Diprotic acid-sulfuric acid is the type of polyprotic acid that can donate two protons per molecule, and it is therefore known as a diprotic acid

• Tripotic acid-phosphoric acid is the type of polyprotic acid, an acid able to donate three protons per molecule

The equations for these reactions are shown below. 

• A solution of phosphoric acid contains H3O+, H3PO4, H2PO4-, HPO42-, and PO43-

• As with most polyprotic acids, the concentration of ions formed in the first ionization is the greatest

• There are lesser concentrations of the respective ions from each succeeding ionization.

A Lewis acid or base accepts or donates a pair of electrons

• The arhenius and Bronsted-Lowry defintions describe most acids and bases

  • Both definitions assume that the acid contains or produces hydrogen ions

• A third acid classification, based on bonding and structure, includes, as acids, substances that do not contain hydrogen at all

• Lewis acid- is an atom, ion, or molecule that accepts an electron pair to form a covalent bond

  • Applies to any species that can accept an electron pair to form a covalent bond with another species

  • The formula for a lewis acid need not include hydrogen. Even a silver ion can be a Lewis acid, accepting electron pairs from ammonia to form covalent bonds

  • Any compound in which the central atom has three valence electrons and forms three covalent bonds can react as a lewis acid

    • It does so by accepting a pair of electrons to form a fourth covalent bond, completing an electron octet

                                    ACID-BASE DEFINITIONS

• Lewis Base- is an atom, ion, or molecule that donates an electron pair to form a covalent bond

  • An anion is a lewis base in a reaction in which it forms a covalent bond by donating an electron pair

• Lewis acid-base reaction- is the formation of one or more covalent bonds between an electron-pair donor and an electron-pair acceptor

• Although the three acid-base definitions differ, many compounds may be categorized as acids or bases according to all three descriptions 

  457-463: vovo

  Brønsted-Lowry reactions involve conjugate acid-base pairs.

  • The Brønsted-Lowry theory is useful for describing acid-base reactions in aqueous solutions

  • When a Brønsted-Lowry acid gives up a proton, the remaining ion or molecule that re-accepts the proton is the conjugate base.

  • Thus, the species that remains after a Brønsted-Lowry acid has given up a proton is the conjugate base of that acid.

  • The species that is formed when a Brønsted-Lowry base gains a proton is the conjugate acid of that base.

  • Brønsted-Lowry acid-base reactions are equilibrium systems (work both ways) involving two conjugate acid-base pairs.

  • In every conjugate acid-base pair, the acid has one more proton than its conjugate base.

  Strength of Conjugate Acids and Bases

  • The extent of the Brønsted-Lowry acid-base reaction depends on the relative strengths of the acids and bases involved.

  • Strong acids readily donate protons, resulting in very weak conjugate bases.

  • Strong bases have little tendency to attack and retain protons, resulting in very weak conjugate acids. 

  • General rule: the stronger an acid is, the weaker the conjugate base, and the stronger the base, the weaker the conjugate acid. (Strong-weak, weak-strong)

  Using Strength to Predict Reactions

  • The relative strengths of acids and bases can be used to predict the outcome of a reaction.

  • The stronger acid reacts with the stronger base to produce the weaker acid and the weaker base.

  • Proton-transfer reactions favor the production of the weaker acid and the weaker base.

  • For an acid-base reaction to form products completely, the reactants must be much stronger acids and bases than the products.

  Some substances act as either acids or bases.

  • Amphoteric: any species that can react as either an acid or a base.

    • Water is a common example.

  • Whether a substance acts as an acid or a base depends on the strength of the acid or base it is reacting with.

    • Strong acid - act as a base

    • Strong base - act as an acid

  -OH in a Molecule

  • Molecular compounds containing OH groups can be acidic or amphoteric

  • Hydroxyl group: covalently bonded -OH group in an acid

  • For a compound to be acidic, a water molecule must be able to attract a hydrogen atom from a hydroxyl group.

    • More likely when O-H is very polar

  • Any feature of a molecule that increases the polarity of the O-H bond increases the acidity of the compound.

  • Small, more electronegative nonmetal atoms at the upper right of the periodic table form compounds with acidic hydroxyl groups.

  • Oxyacids are molecular electrolytes that contain onerous or more O-H bonds, such as chloric and perchloric acids.

  • The number of oxygen atoms bonded to the atom connected to the -OH group affects the compound’s behavior.

    • More oxygen - increase acidity

  • Electronegative oxygen atoms draw electron density away from the O-H bond, making it more polar.

    • Example:

  • In acetic acid, a second oxygen atom is bonded to the carbon atom connected to the -OH group, making it acidic, unlike ethanol.

  Neutralization reactions produce water and a salt.

  • Neutralization reactions involve the reaction of an acidic compound with a basic compound (they neutralize each other)

    • Example:

    • NaHCO3 and H2C4H4O6 produce baking powder

    • When water is added, produces carbon dioxide

  Strong Acid-Strong Base Neutralization

  • Acid-base reactions occur in aqueous solutions between strong acids and strong bases.

    • Example (ngl i was confused by the long example):

   

  

  • In this reaction, there was an equal number of H3O+ and OH- ions and they are fully converted to water. 

  • Both a salt and water were produced.

  • In aqueous solutions, neutralization is the reaction of hydronium ions and hydroxide ions to form water molecules.

  • Salt: An ionic compound composed of a cation from a base and an anion from an acid.

  Acid Rain

  • Industrial processes produce gases like NO, NO2, CO2, SO2, and SO3.

    • These gases dissolve in atmospheric water to produce acidic solutions, resulting in acid rain or snow.

  • Rainwater is normally slightly acidic (very acidic rain is acid rain).

  • Acid rain erodes statues and affects ecosystems, such asthe  water environment and forests

  • Acid rain can decrease the biodiversity of exosystems by eliminating fish populations in lakes and streams.

  • Amendments to the Clean Air Act in 1990 set limits on SO2 emissions from power plants, which have decreased but not eliminated acid rain in the US.
    

Aqueous Solutions and the Concept of pH

471-477: Sage

Self-ionization of water forms hydronium and hydroxide ions

• Hydronium and hydroxide ions are also provided by the solvent, water

Self-ionization of water

• Pure water is an extremely weak electrolyte

  • Water undergoes self-ionization

• Self ionization of water- two water molecules produce a hydronium ion and a hydroxide ion by a transfer of a proton

• The following equilibrium takes place

  • H2O(l) + H2O(l) H3O+ (aq) + OH-(aq)

• Conductivity measurements show that concentrations of H3O+ and OH- in pure water are each only 1.0 x 10⁻⁷  mol/L of water at 25⁰C. 

• The formula of the particular ion or molecule is enclosed in brackets, [ ]. 

• The mathematical product of [H₃O⁺] and [OH⁻] remains constant in water and dilute aqueous solutions at constant temperature

  • This constant mathematical product is called the ionization constant of water, K_w and is expressed by the following equation

    • K_w = [H₃O⁺][OH⁻] 

• For example, in water and dilute aqueous solutions at 25⁰C, the following relationship is valid

  • K_w = [H₃O⁺][OH⁻] = (1.0 x 10⁻⁷)(1.0 x 10⁻⁷) = 1.0 x 10⁻¹⁴

• The ionization of water increases as temperature increases. Therefore the ion product K_w also increases as temperature increases

  • However at any given temperature K_w is always a constant value. 

  • The value 1.0 x 10⁻¹⁴ is assumed to be constant within the ordinary range of room temperatures

Neutral, Acidic, and Basic Solutions

• Because the hydronium ion and hydroxide ion concentrations are the same in pure water, it is neutral 

  • Any solution in which [H₃O⁺]= [OH⁻] is neutral

• Solutions in which the [H₃O⁺] is greater than the [OH⁻] are acidic 

• Bases increase the concentration of OH⁻ in aqueous solutions

• In basic solutions, the [OH⁻] is greater than the [H₃O⁺]. 

Calculating [H₃O⁺] and [OH⁻] 

• Strong acids and bases are considered completely ionized or dissociated in weak aqueous solutions 

NaOH(s) (H₂O) Na⁺(aq) + OH⁻(aq)

• Because NaOH is a strong base, 1 mol of it will yield 1 mol of OH⁻ in an aqueous solution. 

• Therefore a 1.0 x 10⁻² M NaOH solution has an [OH⁻] of 1.0 x 10⁻²M, as shown by the following 

1.0 x 10-2mol NaOH1 L solution x 1 mol OH⁻1 mol NaOH = 1.0 x 10-2 mol OH⁻1 L solution = 1.0 x 10⁻²M OH⁻

Notice that the [OH⁻] is greater than 1.0 x 10⁻⁷ M. This solution is basic

• Because the K_w of an aqueous solution is a relatively constant 1.0 x 10⁻¹⁴  at ordinary room temperatures, the concentration of either ion can be determined if the concentration of the other ion is known

• EX

K_w = [H₃O⁺][OH⁻] = 1.0 x 10⁻¹⁴

[H₃O⁺] = 1.0 x 10⁻¹⁴[OH⁻]= 1.0 x 10⁻¹⁴1.0 x 10⁻²=1.0 x 10⁻¹²M

• The [OH^-], is 1.0 x 10^-2 M, is greater than the [H₃O⁺], 1.0 x 10^-12 M, as is true for all basic solutions

• IN SHORT the [H₃O⁺] is greater than [OH^-] for all acidic solutions and vise versa for {OH^-]

• In order for K_w to remain constant, an increase in either the [H₃O⁺] or the [OH^-] in an aqueous solution causes a decrease in the concentration of the other ion. 

The concentrations of hydronium and hydroxide ions determine pH and pOH

• pH also indicates the hydronium ion concentration of a solution

• The pH of a solution is defined as the negative of the common logarithim of the hydronium ion connetration, [H₃O⁺] 

pH= -log[H₃O⁺]

• The common logarithim of a number is the power to which 10 must be raised to equal the number

• A neutral solution at 25^oC has a [H₃O⁺] of 1 x 10^-7 is -7.0. The pH is determined as follows

pH= -log [H₃O⁺] = -log (1.0 x 10^-7) = -(-7.0) = 7.0

• pOH of a solution is defined as the negative of the common logarithim of the hydroxide ion concentration, [OH^-] 

pOH=-log[OH^-]

• EX: suppose the [H₃O⁺] in a solution is greater than the [OH^-], as is true for acidic solutions.
  For example, the pH of an acidic solution at 25^oC with a [H₃O⁺] of 1 x 10^-6 M is 6.0. 

pH= -log[H₃O⁺] =  -log(1 x 10^-6) = - (-6.0 = 6.0

• As the temperature changes, the exact values will change because the value of K_w changes. However, the relationship pH + pOH = pK_w will remain the same. 

477-481: Em

The sum of a solution’s pH and pOH is always 14

• If you’re given the [H3O+] you can always find the pH and vice versa

• pH represents a logarithm

• Because of this, the number to the LEFT of the decimal of the pH determines where the decimal point is in the [H3O+]

• The amount of sig figs of the [H3O+] value determines how many figures there are to the RIGHT of the decimal point in the pH

• Ex: [H3O+]=1 X 10^-7

•  this value in scientific notation has 1 SIG FIG. Thus, the -log of [H3O+], aka the pH will have 1 DIGIT to the right of the decimal

• pH=7.0

Example 1: Calculating the pH of a solution given the Identity and concentration of the solution

Calculating pH from [H3O+] when [H3O+] is an integral power of ten

• In the simplest types of solution, the value of [H3O+] is an integral power of 10 like 1M or .01 M

• The pH of this type of solution is just the exponent of the [H3O+] with the sign changed

• Ex: [H3O+] = 1X10^-5  → pH=5.0

Calculating the pH from [H3O+] when [H3O+] is NOT an integral power of ten

• Must use your calculator!!

• Sig Fig rules:

•  # of zeros between the decimal point and first sig fig of [H3O+]’s general form is the number to the LEFT of the decimal point in your pH

• # of sig figs of [H3O+] tell you how many places to the RIGHT of the decimal point

• You can always check the accuracy of your pH calculation by estimating the pH using [H3O+] values that have integral numbers as their pH

• Ex: Given [H3O+] = 3.4 X 10^-5

• 3.4 X 10^-5 is between 1 X 10^-4 and 1 X 10^-5

• 1 X 10^-4 = pH of 4.0 and 1 X 10^-5 = pH of 5.0

• Thus, the pH of the given solution must be between 4.0 and 5.0

Example 2: Calculating the pH of a solution given the [H3O+] of the solution

Calculating [H3O+] and [OH-] from pH

• Basic formula: pH=-log[H3O+]

• Since the base of common logs is 10, the antilog of a common log is 10 raised to that number

• ex:  log[H+]=-pH → [H+]=antilog(-pH) → [H+]=10^(-pH)

• When the pH is an integer, the exponent of 10 that gives [H+] is the negative of the pH

• ex: When [H+]=1x10^-7 M, pH=7.0

• ex: When [H+]=1x10^0 M aka 1 M , pH=0

Example 3: calculation [H3O+] given pH that’s an integral number

Example 4: Calculating Hydronium concentration, hydroxide concentration, and acidity given the pH of the solution that’s NOT an integral number

pH Calculations in accordance with Acid and Base Strength

• Because KOH is a soluble ionic compound and a strong base:

• KOH’s molarity directly tells you the [OH-] 

• note that knowing the [OH-] allows you to determine the [H+] and therefore the pH

• The experimental pH of this solution = calculated (theoretical) pH of this solution

• Note that these properties apply to STRONG ACIDS as well, such as HCl hydrochloric acid

• Because CH3COOH’s molecules don’t fully ionize and it’s a weak acid:

• CH3COOH’s molarity (M) does NOT directly tell you the [H+] 

• Thus, the calculated (theoretical) pH of this solution =/= experimental pH of this solution

• To find the [H+] and [OH-], you must find the pH of the solution experimentally

• These properties apply to WEAK BASES as well, such as NH3 ammonia
  
  Lab note: Drano is an arrhenius base

  483-487: pham

  DETERMINING PH AND TITRATIONS

  
  

  Indicators can determine pH, pOH, and strength

  • Approximate value for pH can be determined using acid-base indicators

  • Acid-base indicators: compounds whose colors are sensitive to pH

  • Indicators change colors because they are either weak acids or weak bases

  • A weak acid indicator (HIn) can be represented:

    • HIn ⇌ H+ + In-

  • In- is the anion of the indicator

  • Colors result from the fact that HIn and In- are different colors

  • In- ions are Bronsted bases 

  • Indicator is present in largely nonionized form, HIn

  

  • In basic solutions, OH- ions combine with H+ ions produced by indicator; this makes the indicator molecules to further ionize to makeup the loss of H_ ions

  • Indicator is now largely present in In- (blue)

  
  

  • Transition interval: pH range in which an indicator changes color

  

  
  

  

  
  
  

  • Different pH indicators change color at different pH values

  • Color depends on the amounts of HIn and In- at a given pH

  • Ex: Methyl red changes color between pH 4.4 and 6.2

    • At pH 4.4 or below, the indicator mostly exists as HIn since it is acidic (red)

    • Above pH 6.2, it mostly exists as In- since it is basic (yellow)

  • During the transition interval, the amounts of both forms are the same so the color is resulted due to the mixture of HIn and In-

  
  

  • A pH meter is a more precise tool to measure pH levels

  • pH meter: determines pH level by measuring the voltage between two electrodes that were placed in the solution 

  • Voltage changes as H3O+ concentration changes 

  
  

  Titration is used to determine exact concentrations

  • Neutralization occurs when 1 mol of H3O+ (acid) equally reacts with 1 mol of OH- (base) to create 2 mols of water

    • As we mix two solutions together, solution of H3O+ with red pH indicator red and solution of OH- with blue pH indicator, this would create a neutral solution with a pH indicator of green 

  
  

  • When adding 0.10 mol of NaOH to 1 L of 0.10 M HCl solution, H3O+ and OH- ions will get equally released and combine until the product [H3O+][OH-] returns to the value of 1 x 10^-14

  • NaCl is the product 

  
  

  • Titration: controlled addition and measurement of the amount of a solution of known concentration required to react completely with a measured amount of a solution of unknown concentration 

  • Helps determine the chemically equivalent amounts of acid and base

  
  

  488-493: Vonese

  Equivalence Point

  • Equivalence point: the point at which the two solutions used in a titration are present in chemically equivalent amounts

  • Indicators and pH meters can be used to determine the equivalence point 

    • pH will change readily as the equivalence point is approached

    • If an indicator is used, must change color over a range that includes pH of equivalence point

  • End point of an indicator: the point in a titration at which an indicator changes color

  • Indicators:

    • Litmus: changes at pH 7, but broad color-change internal (pH 5.5-8.0)

    • Bromthymol blue: better, smaller transitional interval (pH 6.2-7.6)

  • Strong-acid/strong-base titration: 

    • The neutralization produces a salt solution with a pH of 7, so indicators that undergo transition at about pH 7 are used

  • Strong-acid/weak-base titrations: 

    • The equivalence point is acidic (pH lower than 7) because the salt formed is a weak acid. 

    • Methyl orange is an example of an indicator used for this 

  • Weak-acid/strong-base titrations: 

    • These reactions produce salt solutions with a pH greater than 7 because the salt formed is a weak base

    • Indicators include Phenolphthalein (turns pink) and Menthyl red (turns red)

  • Weak-acid/weak-base titrations:

    • The pH at the equivalence point can be acidic, basic, or neutral, depending on the relative acid-base strengths

    • Not practical to carry out these transitions because pH value does not change dramatically 

    • No indicator typically used

  • As base is added, the pH changes from a lower numerical value to a higher one.

  • The change in pH occurs slowly at first, then rapidly through the equivalence point, and then slowly again as the solution becomes more basic.

  A standard solution is used to titrate unknowns.

  • Standard solution: The solution that contains the precisely known concentration of a solute

  • To be certain of the concentration of the known solution, a solution must first be compared with a solution of a primary standard

  • Primary standard: a highly purified solid compound used to check the concentration of the known solution in a titration.

  • Known solution is prepared first to give approximately desired concentration before it is determined precisely by titrating carefully measured quantity of the primary standard

  

  
  

  

   Thermochemistry

501-508: Sage

• Thermochemistry- is the study of the transfers of energy as heat that accompany chemical reactions and physical changes

Temperature and heat are related but not identical 

• Calorimeter- the energy absorbed or released as heat in a chemical or physical change is measured in a calorimeter

• Energy given off (or absorbed) during the reaction is equal to the energy absorbed (or given off) by the known quantity of water.

  • Amount of energy is determined from the temperature change of the known mass of surrounding water

• Data collected from calorimetry experiments are temperature changes because energy cannot be measured directly; but temperature, is directly measurable

• Temperature- is a measure of the average kinetic energy of the particles in a sample of matter. 

• The greater the kinetic energy of the particles in a sample, the higher the temperature is and the hotter it feels

• To assign numerical values to temperature, it is necessary to define a temperature scale. 

• For calculations in thermochemistry, we use the Celsius and Kelvin scales. 

  • Celsius and Kelvin temperatures are related by the following equation

K= 273.15 + ^oC

• The ability to measure temperature is thus based on energy transfer; measured in joules

• A joule is the SI unit of heat as well as all other forms of energy

N x m = kg x m2s2

• Heat can be thought of as the energy transferred between samples of matter because of a difference in their temperatures

• Energy transferred as heat always moves spontaneously from matter at a higher temperature to matter at a lower temperature

Energy transfer varies from reaction to reaction

• The quantity of energy transferred as heat during a temperature change depends on the nature of the material changing temperature, the mass of the material changing temperature, and the size of the temperature change

• EX: one gram of iron heated to 100.0^oC and cooled to 50.0^oC in a calorimeter transfers 22.5 J of energy to the surrounding water.

  • But one gram of silver transfers 11.8 J of energy under the same conditions.

  • Difference depends on the metals’ differing capacities for absorbing this energy.

• Specific heat is the amount of energy required to raise the temperature of one gram of a substance by one Celsius degree (1^oC) or one kelvin (1 K) (because the sizes of the degree divisions on both scales are equal)

  • Values of specific heat can be given in units of joules per gram per Celsius degree, J/(g x ^oC), joules per gram per kelvin, J/(g x K), or calories per gram per Celsius degree, cal/(g x ^oC)

• Specific heat is measured under constant pressure conditions, so its symbol, c_p, has a subscripted p as a reminder. In the equation, c_p is the specific heat at a given pressure, q is the energy lost or gained, m is the mass of the sample, and T represents the change in temperature

cp=qm x T

• This equation can be rearranged to give an equation that can be used to find the quantity of energy gained or lost with a change in temperature

Energy Lost or Gained     q=cp m T

Heat energy is transferred during a reaction

• Energy absorbed as heat during a chemical reaction at constant pressure is represented by H. The H is the symbol  for quantity called enthalpy. It is not practical to talk about enthalpy as a quantity, because we have no way to directly measure the enthalpy of a system

• Only changes in enthalpy can be measured. The Greek letter (“delta”) stands for “change in.” 

  • Therefore, H is read as “change in enthalpy”. 

• An enthalpy change is the amount of energy absorbed by a system as heat during a process at constant pressure H = Hproducts- Hreactants

• The enthalpy of reaction is the quantity of energy transferred as heat during a chemical reaction. (HEAT OF REACTION)

Enthalpy of Reaction in Exothermic Reactions

• If a mixture of hydrogen and oxygen is ignited, water will form and energy will be released explosively

• Energy that is released comes from the reactants as they form products

  • Because energy is released, the reaction is exothermic, and the energy of the product, water, must be less than the energy of the reactants. 

• EX: 2 mol of hydrogen gas at room temp are burned, 1 mol of oxygen gas is consumed and 2 mol of water vapor are formed

2H₂(g) + O₂(g) —> 2H₂O(g)

• Experiments have shown that 483.6 kJ of energy are evolved when 2 mol of gaseous water are formed from its elements at 298.15 K. 

• Modifying the chemical equation to show the amount of energy as heat released during the reaction gives the following expression.

2H₂(g) + O₂(g) —> 2H₂O(g) + 483.6 kJ

• This expression is an example of a thermochemical equation, an equation that includes the quantity of energy released or absorbed as heat during the reaction as written

• In  any thermochemical equation, we must always interpret the coefficients as numbers of moles and never as numbers of molecules. 

• The quantity of energy released as heat in this or any other reaction depends on the amount of reactants and products

• The quantity of energy as heat released during the formation of water from H₂ and O₂ is proportional to the quantity of water formed; require twice as many moles of reactants and would release 2x more energy as heat

4H₂(g) + 2O₂(g) —> 4H₂O(g) + 967.2 kJ

• Producing one-half as much water requires one-half as many moles of reactants and releases only one-half as much energy, or ½ x 483.6 kJ. 

H₂(g) + ½ O₂(g) —> H₂O(g) + 241.8 kJ

Enthalpy of Reaction in Endothermic Reactions

• The situation is reversed in an endothermic reaction– products have a larger enthalpy than reactants.

• Decomposition of water vapor is endothermic; it is the reverse of the reaction that forms water vapor

• In endothermic reactions, enthalpy now appears on the reactant side of the thermochemical equation but no changed value

   2H_2,O(g) + 483.6 kJ —> 2H₂(g) + O₂(g)

• The physical states of reactants and products must always be included in thermochemical equations because they influence the overall amount of energy as heat gained or lost. 

  • EX: energy need to decompose water would be greater than 483.6 kJ if we started with ice, becauze extra energy would be needed to go from ice to liquid and then to vapor

Thermochemical Equations

• Thermochemical equations are usually written by designating the value of H

• For exothermic reaction, H is always negative because the system loses energy.

2H₂(g) + O₂(g) —> 2H₂O(g)   H= -483.6kJ

• For endothermic reaction H is always positive because the system gains energy.

2H₂O(g) —-> 2H₂(g) + O₂(g)  H= +483.6kJ

• Since energy as heat is absorbed, the enthalpy of the reactants is lower than the final enthalpy of the products, and H is positive.

• When looking at all the thermochemical equations, consider the following. 

1. The coefficients in a balanced thermochemical equation represent the number of moles of reactants and products and never the number of molecules. They can be fractions when necessary

2. The Physical state of the product or reactant involved in a reaction is an important factor, and, therefore, must be included in the thermochemical equation

3. The change in Enthalpy represented by a thermochemical equation is directly proportional to the number of moles of substances undergoing a change. If 2 mol of water are decomposed, twice as much enthalpy

4. The value of the enthalpy change, H, is usually not significantly influenced by changing temperature

Enthalpy of formation is the energy change when elements form one mole of a compound

• Thermochemical data are often recorded as the enthalpies of such composition reactions. 

• The molar enthalpy of formation is the enthalpy change that occurs when one moles of a compound is formed from its elements in their standard state at 25⁰C and 1 atm. 

• Enthalpies of formation are given for the standard states of reactants and products; usually atmospheric pressure and room temp 298.15K

• To signify that a value represents measurements on substances in their standard states, a ^o sign is added to the enthalpy symbol, giving delta H for the standard enthalpy of a reaction.

• Adding a subscript f, as in Hfo further indicates a standard enthalpy of formation. 

508-514 (start from “exothermic compounds tend to be very stable”): Pham

Exothermic compounds tend to be very stable

• A compound with a large negative enthalpy of formation releases a large amount of energy as heat when it’s formed → stable

• Elements in standard states have ∆H⁰_f = 0

• The majority of enthalpies of formation are negative

• ∆H⁰_f of CO2 is -393.5 kJ/mol therefore, it is more stable than the elements from which it was formed

• Compounds with relatively positive or slightly negative values are unstable

• Ex: HI is a colorless gas that decomposes at room temperature 

  • Has an enthalpy of formation of +26.5 kJ/mol

  • As it decomposes, the violet iodine vapor, I₂, becomes visible through the container 

• Compounds with a high positive enthalpy of formation are very unstable and may react or decompose violently 

• Ex#1: C₂H₂ reacts violently with oxygen and must be stored in cylinders as a solution in acetone

• Ex#2: HgC₂N₂O₂ has a very large enthalpy of formation of +270 kJ/mol which makes it useful as a detonator for explosives

Enthalpy changes in combustion

• Combustion reactions produce energy in the form of light and heat when a substance is combined with oxygen 

• Enthalpy of combustion: the enthalpy change that occurs during the complete combustion of one mole of a substance

• Enthalpy of combustion is defined in terms of one mole of reactant, and enthalpy of formation is defined in terms of one mole of product

• All substances are in their standard states

• General enthalpy notation, ∆H, applies to enthalpies of reaction

• ∆H_c refers to the enthalpy of combustion

• A combustion calorimeter is a common instrument used to determine enthalpies of combustion

• A similar apparatus under constant pressure is used to obtain enthalpy measurements

Change in enthalpy is calculated using Hess’s Law

• Thermochemical equations can be rearranged and added to give enthalpy changes for reactions not included in the data tables

• Hess’s law: the overall enthalpy change in a reaction is equal to the sum of enthalpy changes for the individual steps in the process

• Energy difference between reactants and products is independent of the route 

• Measured enthalpies of reaction can be combined to calculate enthalpies of reaction that are difficult or impossible to actually measure

• Calculate the enthalpy of formation of methane gas from its elements, hydrogen gas and solid carbon (graphite), at 298.15 K: 

  

• In order to calculate the change in enthalpy, we use the combustion reactions of each element 

• Principles for combining thermochemical equations:

1. If a reaction is reversed, the sign of ∆H is also reversed

2. Multiply the coefficients of the known equations so that, when added together, they give the desired thermochemical equation. Multiply ∆H by the same factor as the corresponding equation.

• In this case, since methane is on the right side of the thermochemical equation, we must reverse the combustion equation of methane and change the sign of ∆H. This will turn the reaction to an endothermic one.

• Since we now have 2 moles of water as a reactant, we will need 2 moles of water as a product

• For the combustion of hydrogen, it only produces one mole of water so we would need to multiply everything by 2 

• Now add the three equations together 

• Hess’s law states that the enthalpy difference between reactants and products is independent of the pathway

• Any enthalpy of reaction may be calculated using enthalpies of formation for all the substances in the reaction of interest, without knowing anything else about how the reaction occurs             

Enthalpy of formation is the sum of its sub-reaction enthalpies

• When carbon is burned in a limited supply of oxygen, CO is produced

• Carbon is first oxidized to CO₂ then part of it is reduced with carbon to give some CO

• These two reactions occur simultaneously so we get a mixture of CO and CO₂ 

• It’s not possible to directly measure the enthalpy of formation of CO(g_ from C(s) and O₂(g)

• However, we do know the enthalpy of formation of CO₂ and enthalpy of combustion of CO

• Reverse second equation because we need CO as a product

• This diagram is a model for a reaction that takes place in two steps

• If we plot the reactions based on their relative energy, you can see the relationship among the values for the enthalpy of formation of CCO

• The formation of CO₂ is at a level of -393.5 kJ/mol

• It shows the reverse of the combustion reaction (+293.0 kJ/mol) is added to that level

• The value of the formation of CO is -110.5 kJ/mol.

516-518: Vonese

Driving Force of Reactions

• The change in energy of a reaction system is one of the two factors that allow chemists to predict whether a reaction will occur spontaneously and to explain how it occurs

• The randomness of the particles in a system is the second factor affecting whether a reaction will occur spontaneously

Reactions generally move to a lower-energy state.

• The majority of chemical reactions in nature are exothermic, resulting in products that are more stable and have lower energy than the reactants.

• Reactions naturally tend towards a lower energy state

• Some endothermic reactions can occur spontaneously, indicating that energy (such as continued heating) is not the only factor determining spontaneity

Entropy measures randomness in a system.

•  A naturally occurring endothermic process is melting.

  • Such as an ice cube melting spontaneously at room temperature as energy is transferred from the warm air to the ice

• During melting, the well-ordered arrangement of water molecules in the ice crystal is lost, and a less-ordered liquid phase of higher energy content is formed

• A system that can go from one state to another without a decrease in enthalpy does so with an increase in entropy

• There is a general tendency in nature to proceed in a direction that increases the randomness of a system

• A random system lacks a regular arrangement of its parts. Tendency toward randomness is called entropy.

• Entropy, S, can be defined in a simple qualitative way as a measure of the degree of randomness of the particles, such as molecules, in a system.

• Entropy in states of matter

  • Solids: particles in fixed position, vibrating; randomness is LOW, so entropy is LOW

  • Liquids: particles are moving rapidly and are much farther apart; MORE random, entropy is HIGHER in liquids (compared to solids)

  • Gases: particles are moving rapidly and are much farther apart; MUCH MORE random, entropy is HIGHER in gases

  • General rule: Entropy in gases>>liquids>solids 

    • (exception of liquid mercury, which is less than some solids)

• The entropy of a pure crystalline solid at absolute zero is zero

• As energy is added, randomness of molecular motion increases

• Measures of energy absorbed and calculations that are used to determine absolute entropy (standard molar energy) are kJ/(mol • K)

• Entropy change, which can also be measured, is defined as the difference between the entropy of the products and the reactants.

  • An increase in entropy is + ΔS.

  • A decrease in entropy is - ΔS.

• The process of forming a solution almost always involves an increase in entropy because there is an increase in randomness.

• This applies to mixing gases, dissolving a liquid in another liquid, and dissolving a solid in a liquid

• Example: Sugar in tea

  • Initial: solid sugar has low entropy as molecules are in one region, separate from water molecules

  • Then: after dissolving, sugar molecules are thoroughly mixed throughout tea; both sugar and water can be found anywhere, increasing system’s randomness and + ΔS

Free energy changes determine if a reaction is endothermic or exothermic.

• Processes in nature are driven towards two directions: towards least enthalpy and greatest entropy

• The direction that LOWERS free energy of a system will be the direction natural processes proceed in 

• Enthalpy and Entropy fight for dominance. The dominant factor determines if forward or reverse reaction is favored

• Free energy: the combined enthalpy-entropy function, also known as “Gibbs free energy”

• Assess the tendency of enthalpy and entropy to change 

• Free-energy change: denoted by ΔG; defined as the difference between the change in ΔH and TΔS

Typical Measurements for  this equation

• TΔS: kj or J

• ΔH: kj or J

• ΔG: kj or J

• ΔS: kj/K

There are 4 possible combinations of terms with this formula

Ex1. Exothermic Reaction

Ex2. Endothermic Reaction

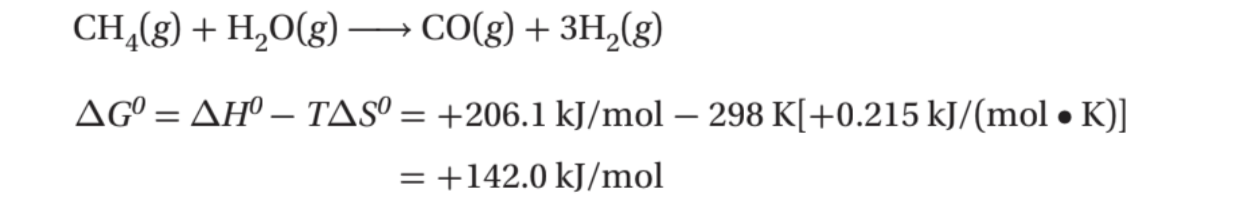
• Even though the entropy increase would normally push the forward reaction to occur spontaneously at room temperature, the positive ΔG tells us otherwise

• Since ΔH is positive, this rxn is endothermic