Matrices

• Lesson 1: Basic Matrix Operations   * Adding and Subtracting Matrices     * A matrix is a rectangular arrangement of numbers     * The dimensions of a matrix with m rows and n columns are m × n (read "m by n")     * The numbers in a matrix are its elements     * Two matrices are equal when their dimensions are the same and the elements are equal     * To add or subtract two matrices, add or subtract their corresponding elements       * Add or subtract matrices only when they have the same dimensions       *   * 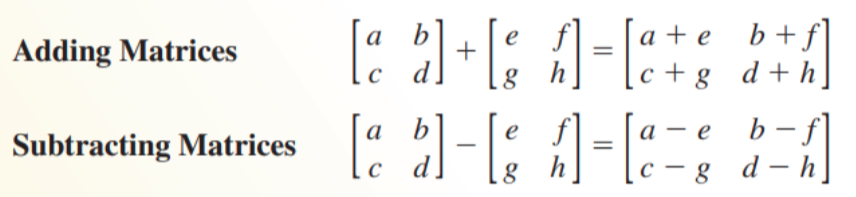Scalar Multiplication     * When working with matrices, a real number is called a scalar     * To multiply a matrix by a scalar, multiply each element in the matrix by the scalar     * This is called scalar multiplication   * Scalar Matrix Equations     * Using the definition of equal matrices, you can equate the elements in corresponding portions of two matrices that are equal
• Lesson 2: Multiplying Matrices   * Multiplying Matrices     * The product of two matrices A  and B is defined provided the number of columns in A is equal to the number of rows in B     * If A is an m × n matrix and B is an n × p matrix, then the product AB is an m × p matrix     *     * To find the element in the ith row and jth column of the product matrix AB, multiply each element in the ith row of A by the corresponding element in the jth column of B, then add the products     *     * 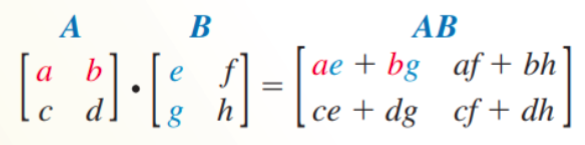Matrix multiplication is not commutative     *
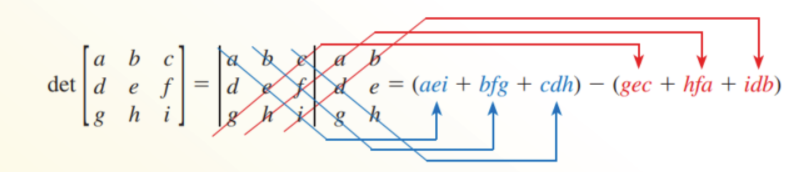
• Lesson 3: Matrix Determinants and Cramer's Rule   * The Determinant of a Matrix     * Determinant of a 2x2 Matrix       * The determinant of a 2x2 matrix is the difference of the products of the elements on the diagonals shown       *     * Determinant of a 3x3 Matrix       * Repeat the first two columns to the right of the determinant       * Subtract the sum of the red products from the sum of the blue products       *     * Cramer's Rule       * You can use determinants to solve a system of linear equations       * The method, called Cramer's Rule, uses the coefficient matrix of the linear system       *       * Cramer's Rule for a 2x2 System         * Let A be the coefficient matrix of the linear system         *         * 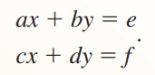If det A ≠ 0, then the system has exactly one solution:         *         * 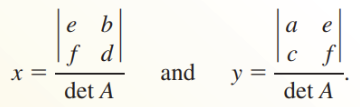Note that the numerators for x and y are the determinants of the matrices formed by replacing the values of the x and y coefficient columns, respectively, with the columns of the constant values       * Cramer's Rule for a 3x3 System         * Let A be the coefficient matrix of the linear system shown below         *         * 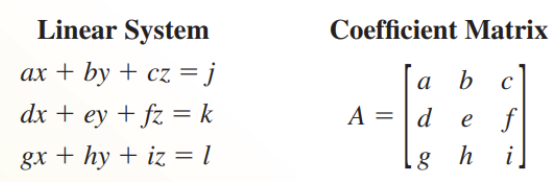If det A ≠ 0, then the system has exactly one solution:         *
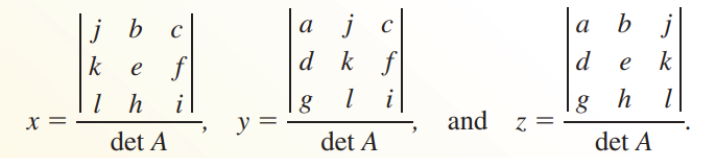
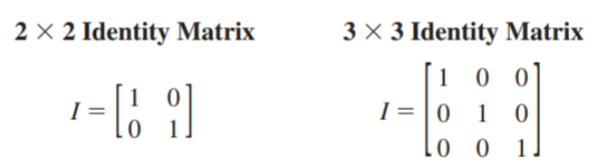
• Lesson 4: Inverse Matrices   * Finding Inverse Matrices     * The n x n identity matrix is a matrix with ones for all elements on the main diagonal (top left to bottom right) and zeros for all the other elements     * If A is any n x n matrix and I is the n x n identity matrix, then AI = A and IA = A     *     * Two n x n matrices A and B are inverses of each other when their product is the n x n identity matrix; AB = I and BA = I     * An n x n matrix A has an inverse if and only if det A ≠ 0     * The inverse of A is denoted by A-1   * The Inverse of a 2x2 Matrix

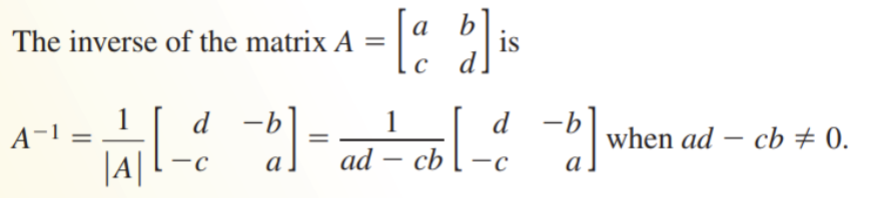
        * Using an Inverse Matrix to Solve a Linear System     * Write the system as a matrix equation AX = B; the matrix A is the coefficient matrix, X is the matrix of variables, and B is the matrix of constants     * Find the inverse of matrix A     * Multiply each side of AX = B by A-1 on the left to find the solution X = A-1B

\