ECMT1020_Lecture_Week_5

How many types of data are there?

• Types of Data:

  • Cross-sectional data: Observations at a single point in time.

  • Time series data: Repeated observations over time on the same entities.

  • Panel data: Combines features of both cross-sectional and time series data, with repeated observations on the same entities over time.

What are the 6 assumptions for regression models with nonstochastic regressors?

• Importance of Assumptions: Necessary to examine the properties of the regression model.

• Key Assumptions:

  • A.1: The model is linear in parameters and correctly specified.

  • A.2: There is variation in the regressor within the sample.

  • A.3: The disturbance term has zero expectation.

  • A.4: The disturbance term is homoskedastic (constant variance).

  • A.5: The values of the disturbance term have independent distributions.

  • A.6: The disturbance term has a normal distribution.

How to find the Unbiasedness of the OLS Regression Coefficients?

• Random Components: Essential for understanding the behavior of OLS estimators.

• Unbiasedness:

  • The OLS regression coefficients are unbiased if the assumptions hold.

  • Normal distribution of regression coefficients occurs if the disturbance term is normally distributed.

Fitted regression coefficient:

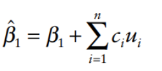
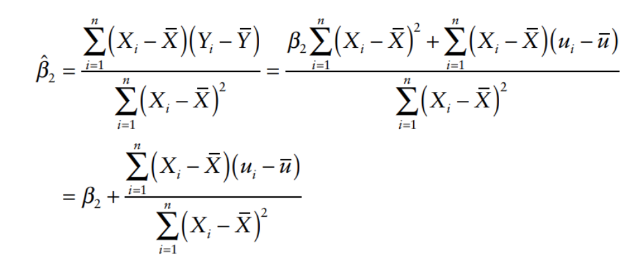
Finding unbiasedness using fitted regression coefficient:

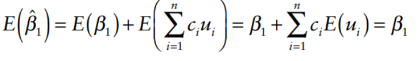
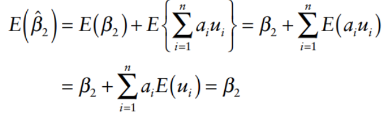
How do you define the precision of the regression coefficients?

• Variances of the Regression Coefficients: Important for understanding the reliability of estimates.

  

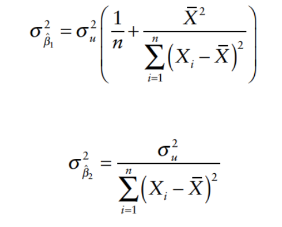
Define the mean square deviation MSD of X:

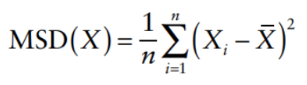
Rewrite variance of b₂ as:

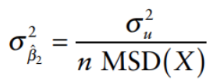
• Standard Errors: Measure the precision of the estimated coefficients.

  

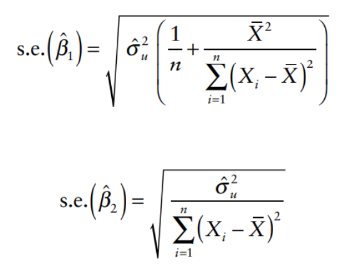
How to test for hypotheses relating to the regression coefficients?

• Hypothesis Testing: Involves testing the significance of regression coefficients.

• T-statistics formula:

  

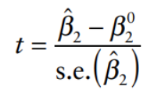
• Degrees of Freedom:

  • In simple regression, degrees of freedom = n - 2 (where n is the number of observations).

  • For multiple regression, a more general expression is required.

• Confidence Intervals: Used to assess the range of values for the regression coefficients.

  

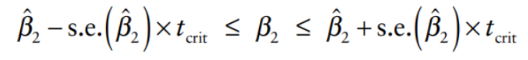
2.7 The F Test of Goodness of Fit

• Purpose: To test the overall

  significance of the regression model.

• How to compute the F-statistic (2 ways):

  

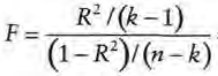
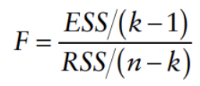
  • k: number of parameters in regression

  • n: number of observations

F statistics is an increasing function of R² (dividing both numerator and denominator by TSS):

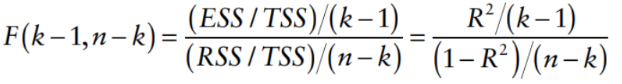
• Key Concepts: Involves comparing the model with a null hypothesis to determine if the model explains a significant amount of variance in the dependent variable.

  • the F-statistic is equal to the square of the t-statistic.

    

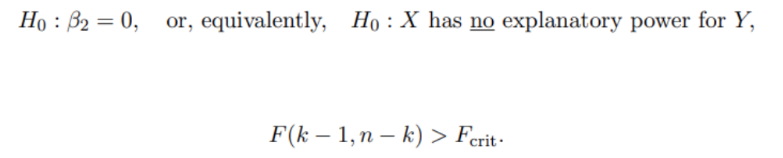
Key Terms

• Ordinary Least Squares (OLS): A method for estimating the parameters in a linear regression model.

• Homoskedasticity: The assumption that the variance of the error terms is constant across all levels of the independent variable.

• Normal Distribution: A probability distribution that is symmetric about the mean, indicating that data near the mean are more frequent in occurrence.