6.2: Binomial and Geometric Probability

Binomial Distributions

• A setting is considered binomial if the four following criteria are met
  • B: Binary
  • Trials must be able to be categorized as successes or failures
  • I: Independence
  • Trials must be independent from one another
  • N: Number
  • There must be a fixed number of trials
  • S: Success
  • There must be a constant probability of success for each trial (represented by variable p)
• Binomial random variables meet all four of these conditions, and are described by binomial distributions
• B(n,p) means that there is a binomial distribution where x counts the number of successes
  • n = number of trials/observations
  • p = probability of success
• x can only take on whole number values from 0 to n
• Mean and standard deviation for binomial random variables
  • µ = np
  • σ = square root of np(1-p)

Formula for Binomial Predictability

• 
• This means that:
  • Out of n trials, there are k successes
  • n choose k counts the number of ways to have successes in n trials
  • p^k calculates the number of times k succeeds
  • (1-p)^(n-k) calculates the number of failures
• Calculator use
  • Particular success = binomPdf
  • Eg. P (x=5)
  • Cumulative success = binomCdf
  • Eg. P (x<5)
  • P(1<x<12)
  • Menu 6→5→D/E
  • Must show equations + work on paper to reflect what is done on calculator for credit on tests + AP exam

Example

• The probability of hitting a bullseye while playing darts is 0.37

• We are going to throw 25 darts and count the number of bullseyes.

• Each throw is independent.

  

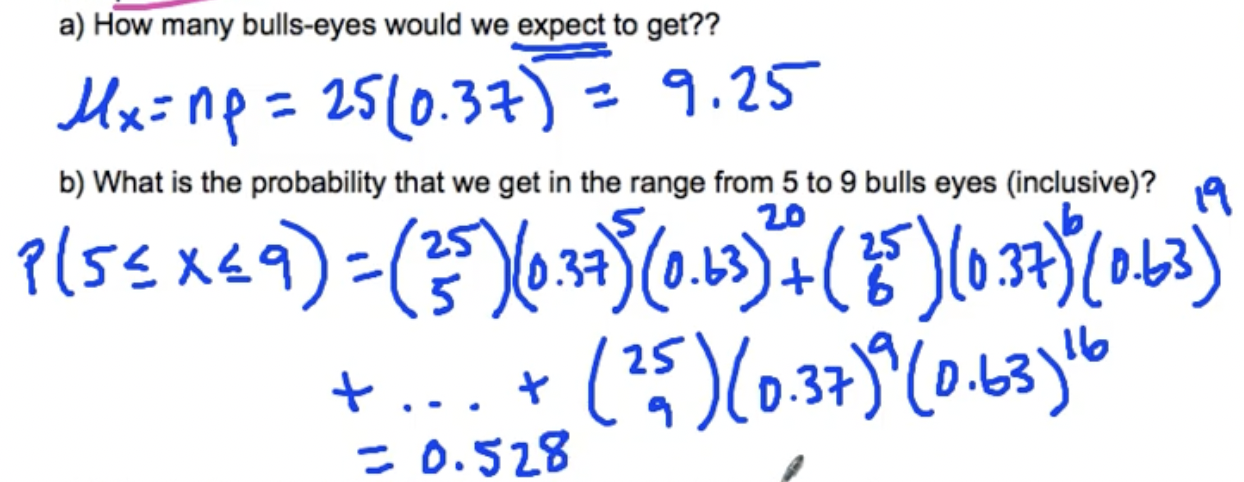
Geometric Distributions

• Meet all of the criteria for binomial probabilities except there is no set number of trials → they are continued until failure
• If x is geometric, p is the probability of success, and 1-p is the probability of failure, then:
  • P(first success on nth trial) = (1-p)^(n-1) x (p)^1
  • We succeeded once (on the last trial) and failed every time before that
  • P(success takes more than n trials) = (1-p)^n
  • We only know we failed this many times

Example

\