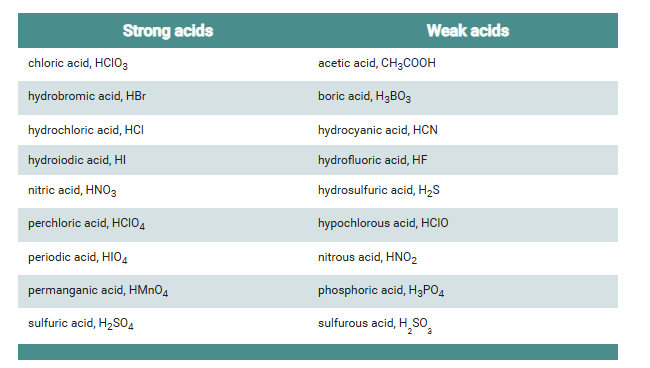
4.2.3 Acids and Bases: Buffers

• Equal amounts of Acetic acid and the acetate ion are used in buffer reactions, at which they are in equilibrium:

  

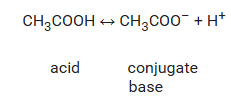
The Henderson-Hasselbalch Equation

• It quantitatively relates pH and concentration.

• It allows for calculation of pH directly from concentrations of the conjugate acid-base pair, and the equilibrium constant.

• pH = pKa + log ([A-] / [acid])

• So it is pH is equal to the equilibrium constant + the logarithm of the concentration of the conjugate base divided by the concentration of the acid.

• Remember, pKa is found through the negative logarithm of the acid dissociation constant (Ka), and Ka is found through an index, which indicates the strength of the acid in solution.

• The lower the pKa value, the stronger the acid, meaning it dissociates more completely in water.

• The higher the Ka value, however, the stronger the acid.

Titration

• Is used to find the concentration of an acid or a base in a solution.

• A titrant is the acid or base that you add to the unknown species in a titration. You know the concentration of the titrant.

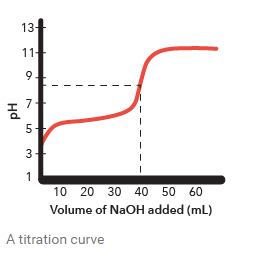
• The equivalence point is at which the pH changes quickly and the titration is complete

• 

Acid-Base Indicators

• Another way to determine the equivalence point is by using an acid-base indicator, as it changes color at the pH of the equivalence point.

• They are either weak acids or weak bases.

• The protonated form refers to the addition of a proton, forming a conjugate acid, while the deprotonated form refers to the removal of a proton, resulting in the corresponding conjugate base.

• If there are excess hydrogen ions and the pH is low, the equilibrium will be shifted in favor of the protonated form of the indicator

• If the hydrogen ion concentration decreases, and the pH is high, then the deprotonated form will be more abundant.

• The equivalence point marks when equal amounts of acid and base have reacted. The number of moles of acid or base has reacted with the equivalent number of moles in the titrant.

• The end point is at the pH at which the indicator changes color.

• The pH of the endpoint of the indicator should be as close as possible to the pH at the equivalence point of the reaction.

Equivalence Points

• The reason why not all equivalence points are at a pH of 7 is because the nature of the acids and bases involved in the reaction, which can result in either acidic or basic solutions at their respective equivalence points.

• Between a strong base and a weak acid, you would want an equivalence point that is above pH 7, reflecting the formation of a basic salt in solution.

• between a weak base and a strong acid, the equivalence point will typically be below pH 7, indicating the presence of an acidic salt in solution.

• Furthermore, when dealing with strong acids and strong bases, the equivalence point will occur at a pH of 7, as the neutralization results in the formation of a neutral solution.

• 

Polyprotic Acid Titration

• Titration curves have one equivalence point for each ionizable hydrogen atom.

• This can be made apparent on the titration curve, as polyprotic acids have 2 or more Ka values.

Finding Different values through titration curve

Finding initial pH

Set up an ICE table, as is done for all equilibrium problems, and use the

equilibrium expression and K a1 to calculate the H + concentration. The negative logarithm of the concentration of H + will yield the initial pH.

pH of solution at half-equivalence points

• The pH at the first half-equivalence point is equal to the negative logarithm of K a1. The pH at the second half-equivalence point is equal to the negative logarithm of K a2.

/

Titration Curves and Buffers

• The buffer zone is the region of the titration curve where the pH remains relatively stable despite the addition of small amounts of acid or base, allowing it to resist changes in pH effectively.

• In the buffer zone, the concentrations of the conjugate acid and base are about equal.

• This means you can translate this back to the Henderson-Hasselbalch equation ( pH = pKa + log( [base-] / [acid] ) ).

• The log of 1 equals zero, so in the buffer zone, the pH equals pKa

• The Buffer Zone is the pKa plus or minus 1

• That means that the acid would be an affective buffer between pKa - 1 and pKa +1.

/

At the halfway point to the equivalence point in the titration, the pH of the solution is equal to the pKa of the acid.

and the pH of the solution is equal to the pKa of the acid

__________________________________________________________________________

Carbonic acid (H2CO3) and the corresponding bicarbonate (HCO3-) has a pKa of 6.38. If the pH of the buffer was 6.05, which species would be in greater quantity?

Given that carbonic acid (H2CO3) has a pKa of 6.38 and the buffer's pH is 6.05, we can analyze the concentrations of the species in the solution using the Henderson-Hasselbalch equation:

pH = pKa + \log \left( \frac{[A^-]}{[acid]} \right)

Substituting the known values:

6.05 = 6.38 + \log \left( \frac{[HCO3^-]}{[H2CO3]} \right)

Rearranging provides:

\log \left( \frac{[HCO3^-]}{[H2CO3]} \right) = 6.05 - 6.38 = -0.33

Converting from logarithmic to linear form yields:

\frac{[HCO3^-]}{[H2CO3]} = 10^{-0.33} \approx 0.47

This indicates that the concentration of HCO3- is lower than that of H2CO3 in the buffer solution. Therefore, since the pH of the buffer (6.05) is lower than the pKa (6.38), it indicates that there are more acidic species present. Thus, H2CO3 (carbonic acid) would be in greater quantity than HCO3-.

To determine which substance exists predominantly in the protonated form at a pH of 4.5, we need to compare the pKa values of the substances to the pH. Generally, when the pH is lower than the pKa, the protonated form is favored. If the substance has a pKa value greater than 4.5, it will be predominantly in the protonated form.

For example:

• Acid A: pKa 5.0 (predominantly protonated)

• Acid B: pKa 4.0 (predominantly deprotonated)

• Acid C: pKa 4.5 (at equilibrium, equal amounts of protonated and deprotonated)

Therefore, any acid with a pKa greater than 4.5 will exist predominantly in the protonated form at this pH, while those with a pKa of less than 4.5 will be mostly in their deprotonated form.

To find the pH of a 0.085 M solution of nitrous acid (HNO2) with a $K_a$ of $4.5 \times 10^{-4}$, we first set up the expression for the acid dissociation:

1. Write the dissociation equation:
   HNO2 \rightleftharpoons H^+ + NO2^-

2. Set up the ICE table for initial concentrations:

   • $[HNO2] = 0.085$ M

   • $[H^+] = 0$ M

   • $[NO2^-] = 0$ M

3. At equilibrium:

   • $[HNO2] = 0.085 - x$

   • $[H^+] = x$

   • $[NO2^-] = x$

4. Substitute into the Ka expression:
   Ka = \frac{[H^+][NO2^-]}{[HNO2]} = \frac{x^2}{0.085 - x} Given $Ka = 4.5 \times 10^{-4}$,
   we can assume that $x$ is small compared to 0.085, allowing us to simplify as $0.085 - x \approx 0.085$:
   4.5 \times 10^{-4} = \frac{x^2}{0.085}

5. Now solve for x:
   x^2 = 4.5 \times 10^{-4} \times 0.085
   x^2 = 3.825 \times 10^{-5}
   x = \sqrt{3.825 \times 10^{-5}} \approx 0.0062

6. Calculate the pH:
   pH = -\log[H^+] = -\log(0.0062) \approx 2.21

Thus, the pH of the 0.085 M solution of nitrous acid is approximately 2.21.

To find the pH of the solution after mixing the solutions of HNO3 and KOH, we first calculate the moles of HNO3 and KOH separately:

1. Calculate moles of HNO3:
   \text{Moles of HNO3} = 1.45 \text{ L} \times 0.056 \text{ M} = 0.0812 \text{ moles}

2. Calculate moles of KOH:
   \text{Moles of KOH} = 0.52 \text{ L} \times 0.13 \text{ M} = 0.0676 \text{ moles}

3. Determine net moles of acid and base:
   Since HNO3 is a strong acid and KOH is a strong base, they will completely react with each other in a 1:1 ratio:

   • After the reaction, the moles of HNO3 remaining will be:
     0.0812 - 0.0676 = 0.0136 \text{ moles of HNO3 remaining}

   • KOH will be completely neutralized because it has a smaller amount.

4. Find the total volume of the mixed solution:
   \text{Total Volume} = 1.45 \text{ L} + 0.52 \text{ L} = 1.97 \text{ L}

5. Calculate the concentration of the remaining HNO3:
   \text{Concentration of HNO3} = \frac{0.0136 \text{ moles}}{1.97 \text{ L}} \approx 0.00691 \text{ M}

6. Find the pH from the concentration of HNO3:
   Since HNO3 completely dissociates in solution, we can find the pH:
   [H^+] = 0.00691 \text{ M} \implies \text{pH} = -\log[0.00691] \approx 2.16

Thus, the pH of the solution after mixing is approximately 2.16.