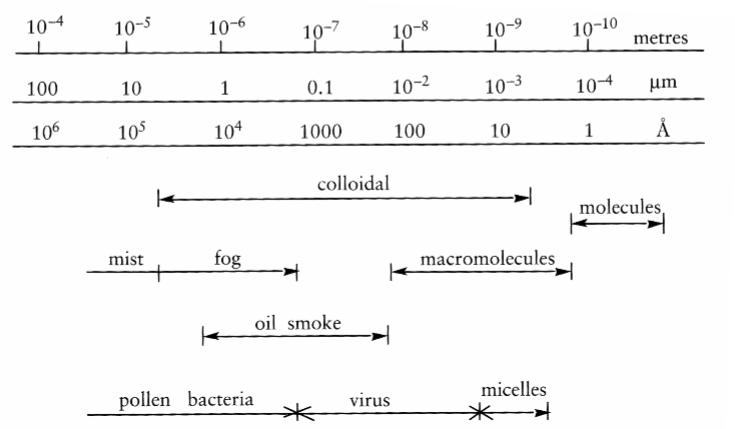
1. Introduction to Surface and Colloid Chemistry
Colloidal molecules and macromolecules-
Colloidal molecules: 1 nm to 1 μm
Macromolecules: 0.1 nm to 10 nm
There is an overlap between colloidal and macromolecules
Colloidal dispersion- A colloidal dispersion is a mixture in which one phase is evenly distributed in the other phase. Two phases are mixed.
- Properties are strongly related to the characteristics of surfaces (usually used for solids) and interfaces (usually used for liquid)
- Colloidal dispersions are meta-stable – stability is a kinetic phenomenon. They will sooner or later collapse.
The solution is dissolved molecules that interact with solvent.
Types of colloidal dispersions
Gas | Liquid | Solid | |
|---|---|---|---|
In a gas | - | (Liquid) aerosol (e.g mist) | (Solid) aerosol (e.g smoke) |
In a liquid | Foam (whipped cream, guinness) | Emulsion (e.g mayonnaise) | Suspension (sol) (e.g paint) |
In a solid | Solid foam (e.g styrofoam) | Solid emulsion (e.g butter) | Solid suspension (e.g ruby glass) |
Difference between a solution and a dispersion
Solutions
- Molecules that are dissolved through interaction with solvent molecules
- Solutions are controlled by inter-molecular interaction and can be thermodynamically stable
Dispersions
- Dispersions are controlled by inter-molecular interaction (in the solution) as well as colloidal forces between interfaces
- Dispersions are practically never thermodynamically stable
- Particles (and aggregates of molecules) are distributed (dispersed) in a continous phase
By reducing particle size → making it more stable. Density of particles should be lower than solvent’s
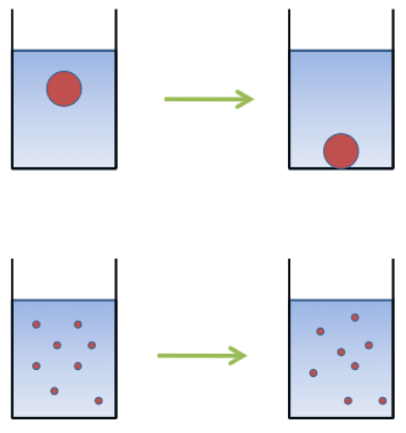
Fundamental forces operate on fine particles in dispersion
• Viscous drag force tries to counteract gravitational force
• Kinetic energy: Brownian motion (self-diffusion of particle) (random displacement of particle)
Gravitational force: Sedimentation
Stokes law: It strongly depends on size. It assumes that there are spherical particles and no interaction between particles.
η counteracted by the dynamic viscosity of continuous phase
Density of particles is higher than solvent’s density → sedimentation
Density of particles is lower than solvent’s density→ rise to the surface of the solvent (creaming)
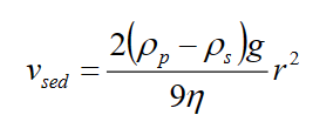
Add polymer →increased viscosity → reduced rate of sedimentation
Reduced size of particle → reduced rate of sedimentation
Kinetic energy
Brownian motion for v<100 cm/s in one direction
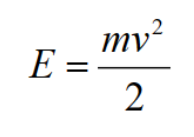
Sedimentation and kinetic energy- For small particles
For small particles: vsed << vkin
Particle size is a crucial property
Kinetic energy:

Sedimentation:

Assume particles with 2x density of water dispersed in water
Brownian motion- Random movement of small particles due to temperature-induced density fluctuations in the surrounding medium. The rate depends on size, temperature and time.
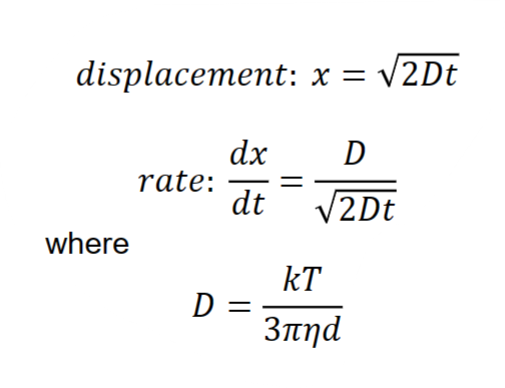
D= diffusion coefficient [m2/s]
k= Boltzmann constant (J/K)=1.38×10−23 J/K
T= temperature (K)
η=dynamic viscosity of continuous phase [Pa•s]
d=hydrodynamic diameter of particle [m]
x=random displacement [m]
Mono- or polydisperse size distribution-
Polydisperse size distribution= many different sizes are present
Polydispersion is the most common
The link between colloids and surfaces
• Colloidal dispersions can have huge surface areas
• Attraction (sticking to each other) or repulsion between particles (surfaces) plays a fundamental role in stability
• The surface properties of the particles determine the interaction
• Many colloidal dispersions need stabilizers which influence the surface properties
Surface tension- The surface tension (surface energy) is a measure of the molecular interactions in a fluid.
- Surface tension arises from an asymmetry in interactions at the surface.
- Excess amount of energy results in surface tension.
- Internal interactions in a liquid make it cohesive
- Stronger interactions in bulk → stronger surface tension
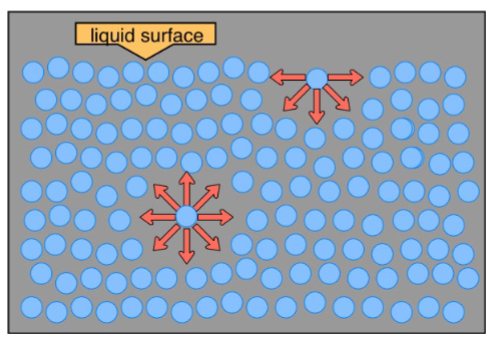
The water molecule at the bottom can interact with all surrounding water molecules, while the water molecule at the surface only can interact with water molecules beside it and beneath
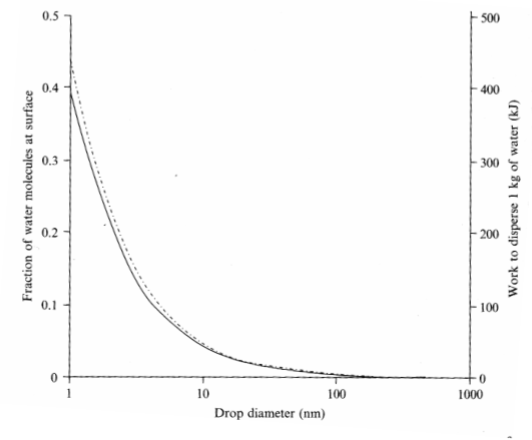
Fraction of water molecules in a water drop that is situated at the surface vs. drop diameter
Smaller diameter → increase surface area → costs energy (work)
Surface tension
- Surface tension (energy) γ is the work to generate the unit area of a new surface.
- Cohesion is the work of cohesion to separate two slabs of a liquid.
- Surface tension is the work demanded for creation of a surface towards air
– Air offer poor opportunities for the liquid molecules to interact
– A measure of the interaction between molecules in a liquid
Air is hydrophobic from point of view of water
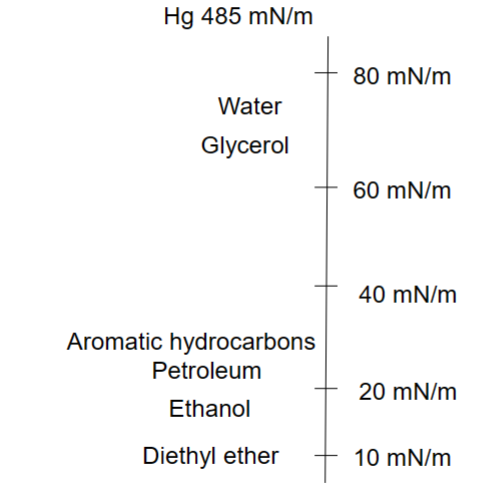
Surface tension of different liquids- Surface tension depends on the molecular interaction in and between the phases.
Mercury has a very strong bond → extremely high surface tension (will not spread out)
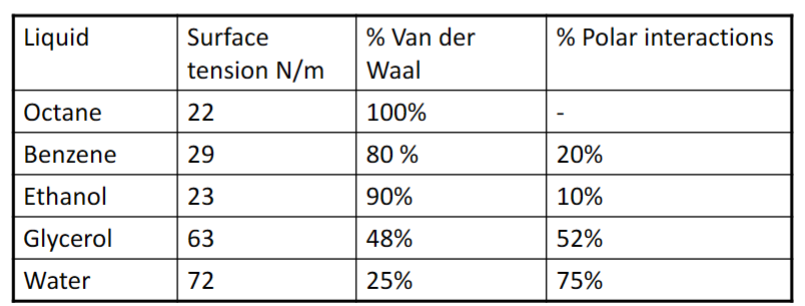
Octane can interact with other molecules because of low surface tension
Curved surface
For example: A small volume of liquid or gas forms a droplet/bubble
- Minimize the surface area (free energy)
- Droplets have an internal pressure (that counteracts this) due to confined molecules in the droplet
- The smaller the droplet (higher curvature of surface) → the higher the pressure (Laplace pressure)
– Equilibrium between minimizing the surface area and internal pressure
Consider an equator cross-section of a sphere
Surface tension causes forces from “north to south” and “south to north”
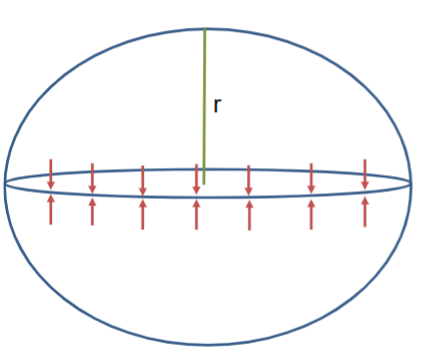
No opposing force → bubble/droplet would collapse → overpressure inside drop
Force from surface tension: Fsurface tension=2𝜋rγ
Force from pressure: FP=ΔP𝜋r2
The forces should be equal so that droplet would collapse: 2𝜋rγ=ΔP𝜋r2
Young-Laplace equation: The relation between pressure and surface tension is generalized in the Young-Laplace equation. The Laplace pressure is the pressure difference between the inside and the outside of a curved surface that forms the boundary between two fluid regions
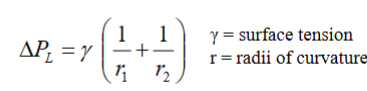
for a spherical droplet/bubble
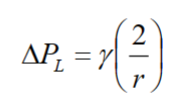
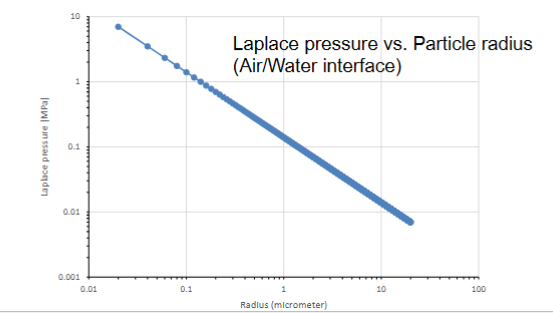
Logarithmic scale for axis
Surface tension (energy) of solid surfaces
High surface tension → things easily spread
Low surface tension → things don’t spread

Surface energy- solid surfaces
• “Fresh” clean surfaces are rapidly contaminated from the surrounding atmosphere.
– Freshly cleaved mica in vacuum: 4500 mN/m.
– Freshly cleaved mica under normal lab conditions: 300 mN/m.
Properties of surfaces
• Surfaces interact differently with liquids depending on their chemical composition
• Change in chemistry of surface (liquid or air for example) → change in surface tension
Spreading- Spreading occurs if the surface energies of the 2 created surfaces γsl + γlv is < initial surface energy γsv
For Teflon: the sum will be larger than initial surface energy → not spreading
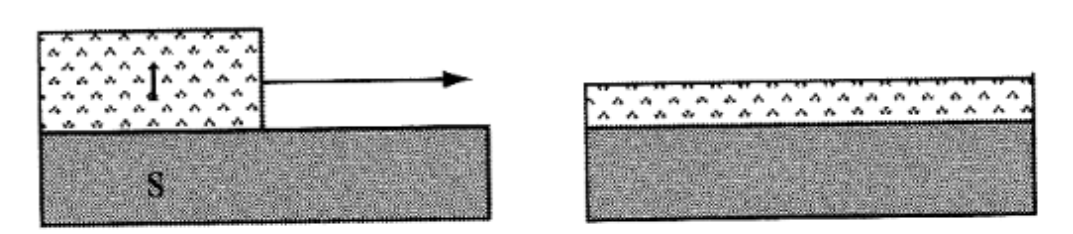
Spreading coefficient:
– S ≥ 0 : spreading occurs
– S < 0 :the liquid forms a finite lens
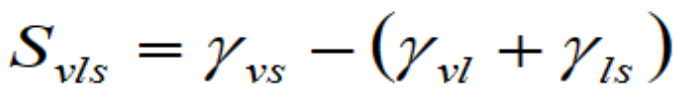
γvs is surface tension between solid and vapor, γvl is surface tension between liquid and vapor and γls is surface tension between solid and liquid
Adhesion- The work to separate two different materials
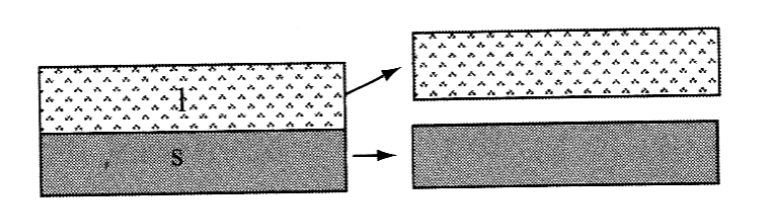
Work of adhesion:
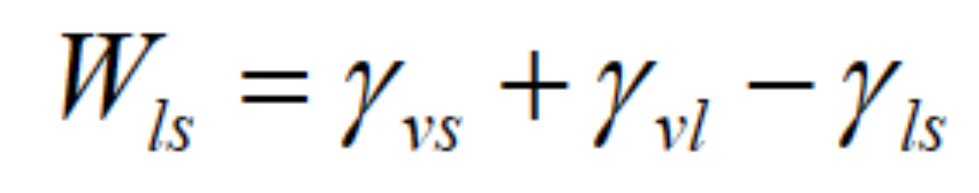
γvs is surface tension between solid and vapor, γvl is surface tension between liquid and vapor and γls is surface tension between solid and liquid
Young’s equation- A small amount of liquid is placed on a surface and a droplet is formed. The contact angle is measure of interaction depends on properties of the liquid and the solid surface
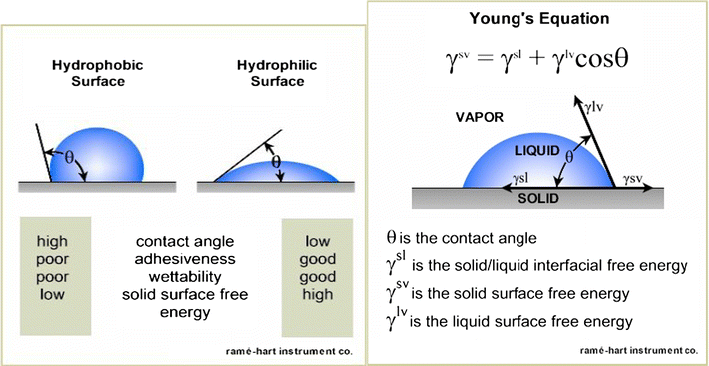
γsv=γsl+γlvcosθ
θ is the contact angle, γvs is solid surface free energy, γvl is liquid surface free energy and γls is solid/liquid interfacial free energy
Example: Water droplet on different surfaces
θ>90o → hydrophobic surface

θ<90o → hydrophilic surface

Extreme examples:
• θ → 0 : water on clean glass.
– Surface groups can form H-bonds with water.
• θ = 150° : Hg on PTFE (polytetrafluorethylene).
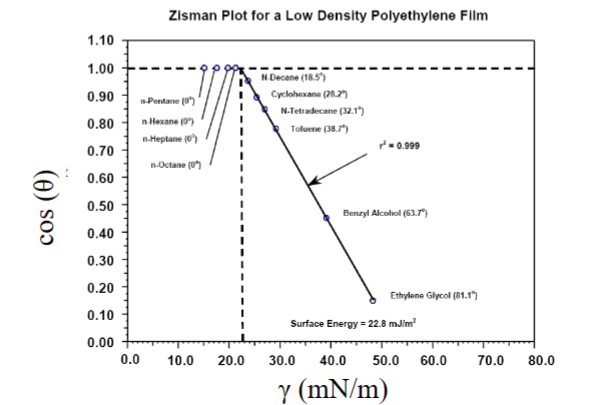
Determination of surface energies – solid surfaces
• For relatively low surface energy surfaces
• Measure contact angles (and surface tension) using different liquids.
– Zisman plot: γsv= γlv of the completely wetting liquid with the highest surface tension
Capillarity
Wetting phenomena can give rise to capillary forces.
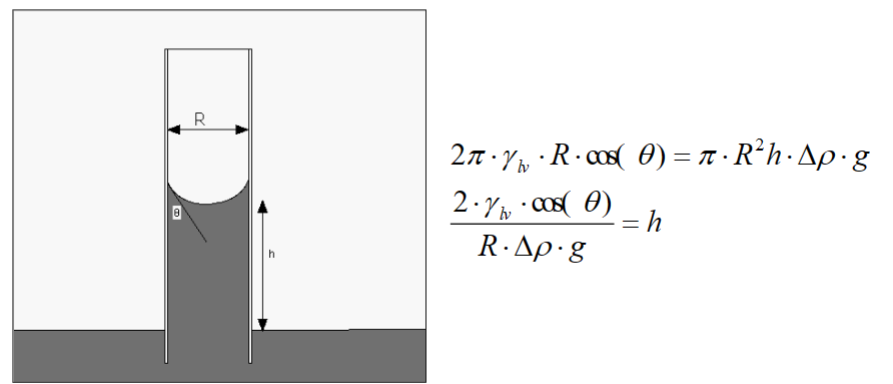
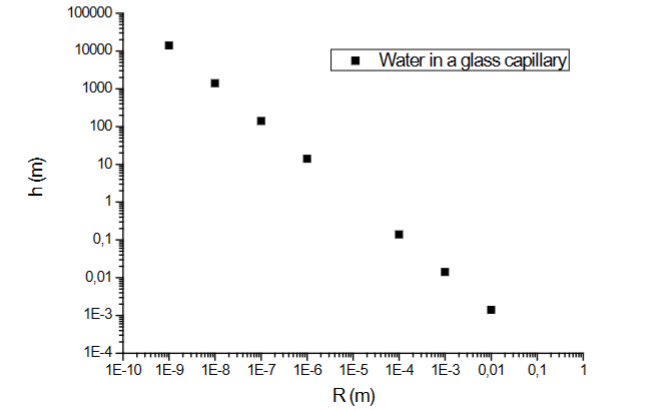
Height of water column (h) vs. capillary radius (r )
Capillary condensation- Vapour condenses in fine pores where the surface is highly curved (wetted surface). Occurs below the saturation vapour pressure of the pure liquid.
• Increased molecular interaction in confined spaces.
– Meniscus formation (Liquid bridge)
– Example: Causes agglomeration of particles (“caking”) in powders.
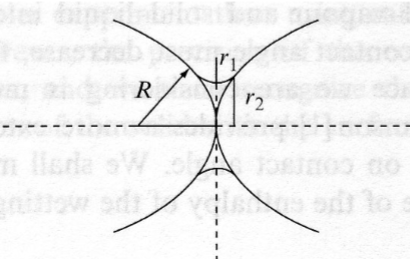
Capillary condensation
• Liquid bridges between wetted solid particles.
• Resulting force: F ≈ 2πRγvl
• Sand castles