Unit 2: Linear Equations
Linear Relationships
Linear equations can be used to represent the relationship between two variables, most commonly x and y. To form the simplest linear relationship, we can make our two variables equal:
y=x
By plugging numbers into the equation, we can find some relative values of x and y.
x | y |
0 | 0 |
1 | 1 |
2 | 2 |
3 | 3 |
If we plot those points in the xy-plane, we create a line.

Every possible linear relationship is just a modification of this simple equation. We might multiply one of the variables by a coefficient or add a constant to one side of the equation, but we'll still be creating a linear relationship.
Linear Functions
Any linear equation with two variables is technically a function. Linear functions are usually written in either slope-intercept form or standard form. We need a thorough and flexible understanding of these forms in order to approach many SAT questions about linear relationships.
Slope-intercept form
The slope-intercept form of a linear function, y = mx + c, where m and b are constants, tells us both the slope (m) and the y-intercept (c) of the line:
The slope:
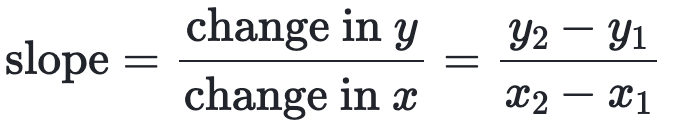
The y-intercept: y value when x = 0.
Standard Form
The standard form of a linear function, Ay+Bx=C, where, A, B, and C are constants, will often be used in word problem scenarios that have two inputs, instead of an input and an output. To find the slope or y-intercept of a line in standard form, it's often most convenient to convert the equation to slope-intercept form by isolating y.
What are systems of linear equations?
A system of linear equations is usually a set of two linear equations with two variables.
x+y=5 and 2x-y=1 are both linear equations with two variables.
When considered together, they form a system of linear equations.
A linear equation with two variables has an infinite number of solutions (for example, consider how (0,5), (1,4), (2,3), etc. are all solutions to the equation x+y=5). However, systems of two linear equations with two variables can have a single solution that satisfies both solutions.
(2,3) is the only solution to both x+y=5 and 2x-y=1.
How does substitution work?
Our goal when solving a system of equations is to reduce two equations with two variables down to a single equation with one variable. Since each equation in the system has two variables, one way to reduce the number of variables in an equation is to substitute an expression for a variable.
To solve a system of equations using substitution:
Isolate one of the two variables in one of the equations.
Substitute the expression that is equal to the isolated variable from Step 1 into the other equation. This should result in a linear equation with only one variable.
Solve the linear equation for the remaining variable.
Use the solution of Step 3 to calculate the value of the other variable in the system by using one of the original equations.
How do I solve systems of linear equations by elimination?
System of equations with elimination
How does elimination work?
Our goal when solving a system of equations is to reduce two equations with two variables down to a single equation with one variable. Since each equation in the system has two variables, one way to reduce the number of variables is to add or subtract the two equations in the system to cancel out, or eliminate, one of the variables.
Sometimes, the system of equations does not have coefficients that readily cancel out.
In this case, we need to find ways to match a pair of coefficients by rewriting one of the equations.
To solve a system of equations using elimination:
Identify a pair of terms in the system that have both the same variable and coefficients with the same magnitude (ex: 2x and 2x, or 3y and 3y). If necessary, rewrite one or both equations so that a pair of terms have both the same variable and coefficients with the same magnitude.
Add or subtract the two equations in the system to eliminate the terms identified in Step 1. This should result in a linear equation with only one variable.
Solve the linear equation to obtain a value for the variable.
Now that you have figured out the value of one variable, plug that value into either equation to find the value of the other variable.
When do I use substitution, and when do I use elimination?
It's up to you!
All systems of linear equations can be solved with either substitution or elimination. On test day, you should use whichever method you're more comfortable with.
Substitution is sometimes easier when:
A variable is already isolated: \[\purpleD{x}=4y+1\]
You can isolate a variable in a single step: \[-3x\purpleD{+y} = 7\]
Elimination is sometimes easier when:
Both equations contain an identical term
The equations contain opposite terms
An equation contains a term that is an integer multiple of a term in the other equation
Linear systems by graphing
Intersections and number of solutions
A linear equation can be represented by a line in the xy-plane. The solution to a system of linear equations is the point at which the lines representing the linear equations intersect.
Two lines in the xy-plane can intersect once, never intersect, or completely overlap. Each of these scenarios corresponds to a different number of solutions to the system of equations the two lines represent.
If the two lines have two different slopes, then they will intersect once. Therefore, the system of equations has exactly one solution.
If the two lines have the same slope but different y-intercepts, then they are parallel lines, and they will never intersect. Therefore, we can say that the system of equations has no solutions.
If the two lines have the same slope and the same y-intercept, then they will completely overlap—they are the same line! When this is the case, we say that the system has infinitely many solutions.
How do I determine the number of solutions for systems of linear equations?
How to determine the number of solutions to a system of equations algebraically
How do I identify the number of solutions?
In the previous section, we covered the graphical method of determining the number of solutions to a system of linear equations. However, when we don't have the aid of a graph, we can determine the number of solutions algebraically.
One way to do it is to rewrite both equations in slope-intercept form, \[y=mx+b\]. This allows us to compare the slopes of the lines, \[m\], and their \[y\]-intercepts, \[b\], to determine the number of solutions.
If the two equations have different \[m\]-values, then the system has one solution.
If the two equations have the same \[m\]-value but different \[b\]-values, then the system has no solution.
If the two equations have both the same \[m\]-value and the same \[b\]-value, then the system has infinitely many solutions.
To determine the number of solutions a system of linear equations has using slope-intercept form, \[y=mx+b\]:
Rewrite both equations in slope-intercept form.
Compare the \[m\]- and \[b\]-values of the equations to determine the number of solutions.
Things to remember
To determine the number of solutions a system of linear equations has using slope-intercept form, \[y=mx+b\]:
Rewrite both equations in slope-intercept form.
Compare the \[m\]- and \[b\]-values of the equations to determine the number of solutions.
If the two equations have different \[m\]-values, then the system has one solution.
If the two equations have the same \[m\]-value but different \[b\]-values, then the system has no solution.
If the two equations have both the same \[m\]-value and the same \[b\]-value, then the system has infinitely many solutions.
What are systems of linear equations word problems?
Systems of linear equations word problems ask us to translate real-world scenarios into a system of two linear equations with two variables. Often, we'll also be asked to solve the system.
This lesson builds upon an understanding of the following skills:
Understanding linear relationships
Solving systems of linear equations
How do I write systems of linear equations?
Word problems that require us to write systems of linear equations have two unknown quantities and two different ways to relate them.
This means we need to write two linear equations, and each contains the two unknowns as variables.
To solve a system of linear equations word problem:
Select variables to represent the unknown quantities.
Using the given information, write a system of two linear equations relating the two variables.
Solve the system of linear equations using either substitution or elimination.
 Knowt
Knowt