Functions

Functions

• A function is a relation that assigns exactly one output for each input.

• Functions are often expressed as equations, ratios, or mappings where each input is associated with one output.

• Common function types include linear, quadratic, polynomial, exponential, and logarithmic.

Volume of a Cylinder

• The formula for the volume (V) of a cylinder is given by: [ V = \pi r^2 h ]

  • Where:

    • ( r ) = radius of the base of the cylinder

    • ( h ) = height of the cylinder

• The volume represents the amount of space inside the cylinder.

Volume of a Cone

• The formula for the volume (V) of a cone is: [ V = \frac{1}{3} \pi r^2 h ]

  • Where:

    • ( r ) = radius of the base of the cone

    • ( h ) = height of the cone

• The volume of a cone is one-third that of a cylinder with the same base and height, reflecting its tapered

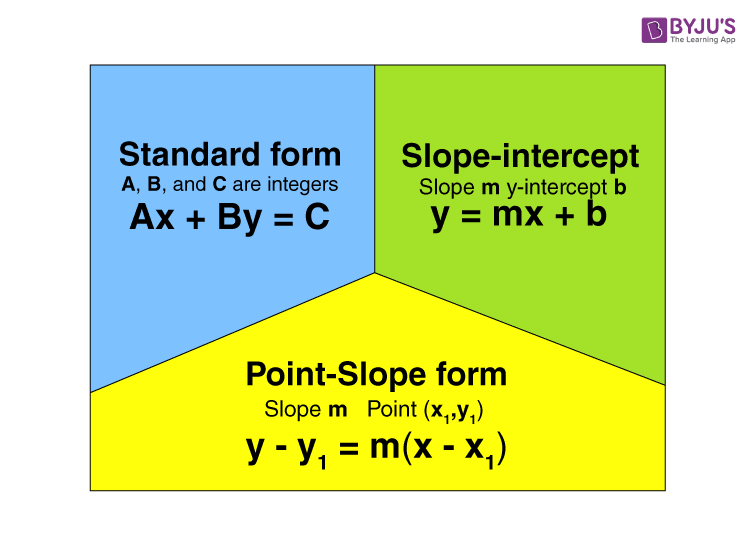
Identifying Linear vs Nonlinear Functions

• Linear Functions:

  • Graphs as straight lines.

  • Can be expressed in the form y = mx + b where:

    • m = slope of the line.

    • b = y-intercept.

  • Have a constant rate of change.

  • Examples include equations like y = 2x + 3.

• Nonlinear Functions:

  • Graphs are not straight lines.

  • Can take forms such as parabolas, circles, or exponential curves.

  • The rate of change is not constant.

  • Examples include y = x^2, y = e^x, or y = sin(x).

Identifying Functions vs Nonfunctions

• Functions:

  • A relation that assigns exactly one output for each input.

  • Passes the Vertical Line Test: If a vertical line intersects the graph in more than one point, it is not a function.

  • Examples include linear functions or basic polynomial functions.

• Nonfunctions:

  • A relation where an input can have multiple outputs.

  • Fails the Vertical Line Test.

  • Examples include circles or any relation where two different y-values correspond to the same x-value.